Download Magnetic fields of stars and planets

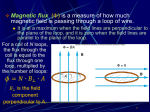
Физика на Земята, атмосферата и космоса
– съвременни проблеми
Магнитното поле на
Земята
Теория и компютърни
симулации
Compass



Chinese were the first ones to use properties of magnetic iron needle to point
out the directions. First information on the use of magnetic compass in Europe
relates to the end of XII century.
In 1600, A.D. William Gilbert, Queen Elizabeth's physician, shed light on the
mystery by showing that "the terrestrial globe itself is a great magnet."
Is the Earth a giant magnet?
where magnetic line is as follows
Magnetic poles of the Earth move!




1741 Hiorter and Anders Celsius
note that the polar aurora is accompanied by a disturbance of the magnetic needle.
1820 Hans Christian Oersted discovers electric currents create magnetic
effects. André-Marie Ampère deduces
that magnetism is basically the force
between electric currents.
1859 Richard Carrington in England
observes a solar flare; 17 hours later a
large magnetic storm begins.
During 16-17 centuries English
discovered that declination of the
Earth’s magnetic field changed. It can
be treated as moving of the magnetic
poles.
Sun is also a magnet
 The
Sun
Sunspots
A sunspot is an area on the Sun's surface (photosphere)
that is marked by intense magnetic activity, which inhibits
convection, forming areas of reduced surface temperature.

Sun and Earth magnetic fields
and solar winds
Now we know that the Sun magnetic field and that of
the Earth interact via solar wind.
The Earth interior
Maxwell and Ohm’s equations
Here B and E are the intensities of the magnetic and electric fields and j is
the space density of the electric current. Values
are respectively
the density of the electric charges, light velocity and conductivity of the liquid.
Magneto-hydrodynamic approximation
The main feature of the magneto-hydrodynamic approximation is the smallness
of parameter
. The electrical field in this approximation is small (E ~
(v/c) B) and so the third Maxwell equation converts into
Nevertheless, E plays an essential role in the Ohm’s equation
since both terms in its rhs are of the same order. Combining then the Maxwell
and Ohm’s equations we obtain the Induction equation:
where
is the magnetic diffusivity.
Divergences
Curls. (Magnetic Field)
Here we remind about sunspots
Induction equation 1
in the Euler
and Lagrange
forms.
Here η is the magnetic diffusivity and
is the so called substantial time derivative i.e. derivative in respect of a moving
liquid element and
Simplification: Induction equation without flow
Induction equation without flow 2
The same process can be seen from another point
of view. The electrical current supporting the field
disappears and so the magnetic field vanishes.
Induction equation without flow 3
How long is the typical time of attenuation
Simple estimation:
What about the typical time for the Earth
Direct solution shows that this time is
almost 10 times overestimated:
in a body with typical size ?
?
Simplification 2: Induction equation
with uniform flow
In the presence of uniform flow velocity, the first term in lhs of the Induction equation
vanishes:
If the time intervals are small, then this equation takes the form:
This means that a solid body when moving progressively,
transfers its magnetic field. Moreover, the rotation of a solid
body does not change its field either. So the Earth moving in
its orbit and rotating at its axis keeps its magnetic field.
Is this strange? - Not so much: The
Earth carries away the electrical currents in its core. So the geomagnetic
poles rotate over the geographic ones.
Frozen magnetic field
By analogy with Reynolds number
Reynolds number
MHD enters the so called magnetic
. During the process of the flow distance
between two liquid points changes. Induction
equation shows in the case when R m  
magnetic field changes being proportional :
liquid contour
magnetic line
~
Lorentz force
in the case of
large magnetic Reynolds number plays the
of elastic force and respectively energy of
the flow converts into magnetic energy by
stretching of line of force of the field. In the
of small magnetic Reynolds number this
force converts into friction one:
. When a star converts into neutrons one its
density enhances with many orders of magnitude. What about its magnetic field?
Frozen magnetic field:
Solar wind and magnetosphere
Momentum equation
Thus magnetic field can be created only by the flow of the conducting fluid. How can this flow
be determined? From the second Newton’s law
one can obtain the momentum equation of Navie-Stocks for the flow:
It shows that a liquid parcel moves being driven by the pressure and Coriolis forces,
by the Archimedean and Lorenz forces
and by the viscid force.
Here , , , , ,
and  are, respectively, the flow velocity, intensity of magnetic
field, density of electric current, temperature deviations, pressure, angular velocity of the
Earth and is the coefficient of thermal expansion. Acceleration, a, of the liquid parcel has
the form:
Heat transport equation in
Boussinesq approximation
The Archimedean force, which is proportional to the density deviations is the driving force
of convection. These deviations depend on the temperature and pressure and as the Boussinesq approximation is applied for liquids, their dependence on pressure is neglected.
Correspondently the Archimedean force takes the form:
, where
are temperature deviations,
is the density, g is the gravitational acceleration.
is the coefficient of thermal expansion under constant pressure.
The substantial derivative here means the times derivative in respect of a moving small
element of liquid. This element loses heat due to diffusion, but it is heated by the internal
source Q. So it is not the cooling teapot.
Whole set of the geodynamo equations
Heat sources: solidification on ICB
radioactive heating
In most computer simulations geodynamo is supported by heat flux from the inner core boundary.
The problem is to define 11 values: three vector fields
and two scalar fields ,
.
Adiabatic reference state
The Boussinesq approximation neglects the density changes of a liquid element due to its
compressibility. Is this assumption adequate to the Earth’s core where density changes are
of order of ~ 20% between bottom and top boundaries? Let us consider the conditions for
existing of convection. The whole set of the reference state equations is given by PREM.
and
is the specific heat
under constant pressure. The differentials here are:
Heat sources: solidification on ICB and
radioactive heating
If the liquid element rises without heating, then its
entropy does not change, dS = 0. So we obtain the
equation for the temperature of the Adiabatic reference state:
Liquid core (Fe)
Solid core (Fe)
Adiabatic and Archimedean cooling
What is the physical meaning of the new terms obtained above? The gradient of adiabatic
temperature creates adiabatic heat flux with surface density :
The whole adiabatic heat flux increases with r:
This is possible only in the presence of the heat support.
Due to the small compressibility (~ 20%) of the liquid in the core
this source happens to be approximately uniform:
Thus, the term
in the equation for the super-adiabatic temperature plays the role
of cooling. We call it the adiabatic cooling. Another new term, taking into account the equation for the adiabatic temperature can be written in a form
where
is the rate of the Archimedean work. Thus this term describes cooling due to the work of the
Archimedean force.
Heat fluxes in the Earth’s core
Convection exists only if the reference state is adiabatic one. The adiabatic temperature profile
creates the adiabatic heat flux (AHF) which increases with r. In absence of radioactive heating
the only source for it is the super-adiabatic heat flux (SHF). Thus AHF plays the role of coling
SHF. Energy of SHF can converts into other types of energy e.g. in the magnetic one. It is alive
flux. Energy of AHF is dead. It is the energy which irreversible converts into heat. In the Earth’s
core main part of SHF converts SHF and so value of SHF decreases ~ 20 times.
AHF:
SHF:
30
CMB
ICB
CMB
Whole heat flux
Boussinesq heat flux
Super-adiabatic heat flux
20
10
Adiabatic heat flux
ICB
0
1.5
2.0
2.5
x1000 km
3.0
3.5
r
Heat transport equation in
Incompressible approach
Heating of the moving liquid element is proportional to its entropy changes.
Its entropy increases with the temperature and decreases with enhancing of pressure
The pressure term and space dependence of the referent temperature are the essential differences with
BA which neglects compressibility. After some thermodynamic and some algebra we obtain the heat
transport equation for the Incompressible approach:
What is the physical meaning of these (underlined) new terms?
Incompressible approach
Energy equations
Sum of these equation yields the conservation law for the whole energy:
Only the heat energy conserves in the Boussinesq approximation:
Boussinesq onset of the convection
Very important difference between BA and IA is the onset of convection. The amplitudes of the
onset flow are small and so the quadratic terms must be neglected in the equations:
Then these equations become linear:
Their solution can be searched in an exponential form:
Then we obtain uniform algebraic equations for and
. Equalizing the determinant of this system to
zero, we obtain the dependence of the frequency from k. Then, using the boundary conditions, we obtain
the dependence of the frequency from the heat flux on the bottom boundary. Equalizing the imaginary
part of the frequency to zero, we obtain the heat flux for the onset of the convection. All this discussion is
based on the uniformity of the equations. However, IA shows that they are not uniform:
Amplitudes of the convection
Thus Boussinesq approximation neglects the work over the flow. Therefore, the amplitudes of the flow
velocity and magnetic field are infinitesimally small in this approximation . In IA the essential part of
the heat energy converts into magnetic one and so its amplitudes are not negligible.
Under integration over the whole space, the lhs of the last equation gives the changes of the whole magnetic energy. The first term in rhs describes the flux of the magnetic energy across CMB. Both these terms
vanish under averaging this equation over long time period. Then we obtain:
The rate of work of the Archimedean force can be estimated from the equation for adiabatic
temperature. It is proportional to the rate of heat production on ICB:
It is remarkable that the efficiency of the dynamo appears to be of order of the Carnot efficiency. From
here we obtain the estimate for the amplitude of the magnetic field, which is in a good agreement with
the direct observation.
Boussinesq and Incompressible approaches
IA
BA
Adiabatic cooling
Taken into account. Diminishes activity of the heat flux in
the direction from ICB to CMB
Not taken into account
Law of energy
conservation
The whole energy is
conserved
Only the internal energy is
conserved
Amplitudes of the flow
All values, V, B and
are
defined by the heat flux.
is defined by the heat flux.
V and B are undefined.
Ohmic dissipation and
Archimedean cooling
Taken into account in the heat
transport equation.
Redistributes heat sources.
Cannot be taken into account in
the heat transport equation.
Boussinesq onset of the
convection
Impossible
Possible
Experiments
Impossible
Possible
Boussinesq and Incompressible approaches
IA
BA
Адиабатично охлаждане
Отчита се. Намалява актив- Не се отчита
ността на топлинен поток в
напраление от ICB към CMB
Запазване на енергията
Пълната енергия се запазва
Запазва се само топлинната
енергия
Амплитуди на
решението
Всички амплитуди, V, B и
се определят чрез топлинен
поток.
се определя чрез топлинен
поток. V and B са неопределени по принцип.
Токова диссипация и
Архимедово охлаждане
Отчитат се в уравнението
за топлопренасяне.
Преразпределя топлинните
източниците
Не се отчитат в уравнението
за топлопренасяне.
Внезапно възбуждане на
конвекцията
Не е възможно.
Възможно е.
Експерименти
Истински IA експеримент не
е възможен
Всички експерименти са от
Буссинесков тип.
Computer simulation of geodynamo
БЛАГОДАРЯ!