* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Functional Mapping - Center for Statistical Genetics
Site-specific recombinase technology wikipedia , lookup
Human genetic variation wikipedia , lookup
Pharmacogenomics wikipedia , lookup
Genetic engineering wikipedia , lookup
Genetic testing wikipedia , lookup
Genome (book) wikipedia , lookup
Gene expression programming wikipedia , lookup
Population genetics wikipedia , lookup
Public health genomics wikipedia , lookup
Designer baby wikipedia , lookup
Behavioural genetics wikipedia , lookup
Microevolution wikipedia , lookup
Heritability of IQ wikipedia , lookup
Functional Mapping
A statistical model for mapping dynamic genes
Recall: Interval mapping for a univariate trait
Simple regression model for univariate trait
Phenotype = Genotype + Error
yi
=
xij + ei
xi is the indicator for QTL genotype
j is the mean for genotype j
ei ~ N(0, 2)
! QTL genotype is unobservable (missing data)
A simulation example (F2)
The overall trait distribution is composed of three distributions, each one coming from
one of the three QTL genotypes, QQ, Qq, and qq.
Trait distribution
500
Overall trait distribution
300
QQ
100
200
qq
0
Frequency
400
Qq
0
5
10
Trait value
15
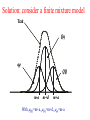
Solution: consider a finite mixture model
Trait
Qq
qq
QQ
m-a
m+d
m+a
With QQ=m+a, Qq=m+d, qq=m-a
We use finite mixture model for
estimating genotypic effects (F2)
yi ~ p(yi|,) = 2|if2(yi) + 1|i f1(yi) + 0|i f0(yi)
QTL genotype (j)
QQ
Qq
qq
Code
2
1
0
where fj(yi) is a normal distribution density
with mean j and variance 2
= (2, 1, 0)
= QTL conditional probability
given on flanking markers
Data Structure
Marker (M)
Subject
1
2
3
4
5
6
7
8
M1
AA(2)
AA(2)
Aa(1)
Aa(1)
Aa(1)
Aa(1)
aa(0)
aa(0)
M2
BB(2)
BB(2)
Bb(1)
Bb(1)
Bb(1)
bb(0)
Bb(1)
bb(0)
…
…
...
...
...
...
...
...
…
Conditional probability
Mm
Phenotype
(y)
y1
y2
y3
y4
y5
y6
y7
y8
of QTL genotype
QQ(2) Qq(1) qq(0)
2|1
2|2
2|3
2|4
2|5
2|6
2|7
2|8
1|1
1|2
1|3
1|4
1|5
1|6
1|7
1|8
0|1
0|2
0|3
0|4
0|5
0|6
0|7
0|8
Human Development
Robbins 1928, Human Genetics, Yale University Press
Tree growth
Looks mess, but there
are simple rules
underlying the
complexity.
The dynamics of gene expression
• Gene expression displays in a dynamic fashion
throughout lifetime.
• There exist genetic factors that govern the
development of an organism involving:
– Those constantly expressed throughout the lifetime (called
deterministic genes)
– Those periodically expressed (e.g., regulation genes)
• Also environment factors such as nutrition, light and
temperature.
• We are interested in identifying which gene(s)
govern(s) the dynamics of a developmental trait using
a procedure called Functional Mapping.
Stem diameter growth in poplar trees
Ma et al. (2002)
Genetics
Poplar tree - height & diameter
Mouse growth
50
45
40
35
Weight
30
25
20
15
10
5
0
1
2
3
4
5
6
7
8
9
10
Week
A: male; B: female
Developmental Pattern of Genetic Effects
QQ
Qq
QQ
Qq
QQ
Qq
QQ
Qq
Wu and Lin
(2006) Nat.
Rev. Genet.
Parents AA aa
Data Structure
Marker (M)
Sample
2
Phenotype (y)
… m
2
…
t1 t2
… tT
y1(1) y1(2) … y1(T)
1
1
2
2
2
2
...
y2(1) y2(2) … y2(T)
3
1
1
…
y3(1) y3(2) … y3(T)
4
1
1
…
y4(1) y4(2) … y 4(T)
5
1
1
…
y5(1) y5(2) … y5(T)
6
1
0
…
y6(1) y6(2) … y6(T)
7
0
1
…
y7(1) y7(2) … y7(T)
8
0
0
...
y8(1) y8(2) … y8(T)
F1
Aa Aa
F2
AA Aa aa
¼ ½ ¼
Conditional probability
of QTL genotype
QQ(2) Qq(1) qq(0)
2|1
2|2
2|3
2|4
2|5
2|6
2|7
2|8
1|1
1|2
1|3
1|4
1|5
1|6
1|7
1|8
0|1
0|2
0|3
0|4
0|5
0|6
0|7
0|8
Mapping methods for dynamic traits
• Traditional approach: treat traits measured at each time point as a
univariate trait and do mapping with traditional QTL mapping
approaches such as interval or composite interval mapping.
• Limitations:
– Single trait model ignores the dynamics of the gene expression
change over time, and is too simple without considering the
underlying biological developmental principle.
• A better approach: Incorporate the biological principle into a
mapping procedure to understand the dynamics of gene expression
using a procedure called Functional Mapping (pioneered by Wu
and group).
Functional Mapping (FunMap)
A general framework pioneered by Dr. Wu and his
colleagues, to map QTLs that affect the pattern and
form of development in time course
- Ma et al., Genetics 2002
- Wu et al., Genetics 2004 (highlighted in Nature
Reviews Genetics)
- Wu and Lin, Nature Reviews Genetics 2006
While traditional genetic mapping is a combination between
classic genetics and statistics, functional mapping combines
genetics, statistics and biological principles.
Data structure for an F2
population
Phenotype
Marker
_______________________________
________________________________________
Sample
y(1)
y(2)
…
y(T)
1
2
…
m
_____________________________________________________________________________________
1
y11
y21
…
yT1
1
1
…
0
2
y12
y22
…
yT2
-1
1
…
1
3
y13
y23
…
yT3
-1
0
…
1
4
y14
y24
…
yT4
1
-1
…
0
5
y15
y25
…
yT5
1
1
…
-1
6
y16
y26
…
yT6
1
0
…
-1
7
y17
y27
…
yT7
0
-1
…
0
8
y18
y28
…
yT8
0
1
…
1
n
y1n
y2n
…
yTn
1
0
…
-1
There are nine groups of two-marker genotypes, 22, 21, 20, 12, 11, 10, 02, 01 and
00, with sample sizes n22, n21, …, n00;
The conditional probabilities of QTL genotypes, QQ (2), Qq (1) and qq (0) given
these marker genotypes 2i, 1i, 0i.
Univariate interval mapping
n
L(y) =
i 1
2i
f 2 ( yi ) 1i f1 ( yi ) 0i f 0 ( yi )
1
( y )2
j=2,1,0 for QQ, Qq, qq
exp{ i2 2j }
2
The Lander-Botstein model estimates (2, 1, 0, 2, QTL position)
fj(yi) =
Multivariate interval mapping
n
L(y) =
f (y i ) 1i f1 (y i ) 0i f 0 (y i )
2i 2
i 1
Vector y = (y1, y2, …, yT)
fj(yi) =
1
(2 )
T/2
1/2
exp{ 12 (yi u j )T 1 (yi u j )}
Vectors
uj = (j1, j2, …, jT)
Residual variance-covariance matrix =
12 1T
2
T 1 T
The unknown parameters: (u2, u1, u0, , QTL position) [3T + T(T-1)/2 +T parameters]
Functional mapping: the framework
Observed phenotype: yi = [yi(1), …, yi(T)] ~ MVN(uj, )
Mean vector: uj = [μj(1), μj(2), …, μj(T)], j=2,1,0
(Co)variance matrix:
2 (1) (1,2)
2
(2,1) (2)
Σ
(T ,1) (T ,2)
(1, T )
(2, T )
2
(T )
Functional Mapping
Functional mapping does not estimate (u2, u1, u0, )
directly, instead of the biologically meaningful
parameters.
An innovative model for genetic dissection of
complex traits by incorporating mathematical aspects
of biological principles into a mapping framework
Provides a tool for cutting-edge research at the interplay
between gene action and development
The Finite Mixture Model
L( , p ,q |M, y)
n
2|i f2 (yi ) 1|i f1 (yi ) 0|i f0 (yi )
i1
Three statistical issues:
Modeling mixture proportions, i.e.,
genotype frequencies at a putative QTL
Modeling the mean vector
Modeling the (co)variance matrix
Modeling the developmental
Mean Vector
• Parametric approach
Growth trajectories – Logistic curve
HIV dynamics – Bi-exponential function
Biological clock – Van Der Pol equation
Drug response – Emax model
• Nonparametric approach
Lengedre function (orthogonal polynomial)
Spline techniques
Example: Stem diameter growth in poplar trees
Ma, et al.
Genetics
2002
Logistic Curve of Growth – A Universal
Biological Law (West et al.: Nature 2001)
Modeling the genotypedependent mean vector,
uj = [uj(1), uj(2),…, uj(T)]
aj
aj
aj
= [ 1b e , 1b e , …, 1b e
r j
j
2 r j
j
j
Tr j
]
Instead of
estimating mj,
we estimate curve
parameters
p = (aj, bj, rj)
Number of parameters to be estimated in the mean vector
Time points
Traditional approach
Our approach
5
3 5 = 15
33=9
10
3 10 = 30
33=9
50
3 50 = 150
33=9
Modeling the Covariance Matrix
Stationary parametric approach
Autoregressive (AR) model with log transformation
1
=
2
T 1
1
2
1
T 2
T 3
T 1
T 2
T 3
1
Nonstationary parameteric approach
Structured antedependence (SAD) model
Ornstein-Uhlenbeck (OU) process
Functional interval mapping
n
L(y) =
f (y i ) 1i f1 (y i ) 0i f 0 (y i )
2i 2
i 1
Vector y = (y1, y2, …, yk)
f2(yi) =
f1(yi) =
f0(yi) =
u2 = (
1
1/2
exp{ 12 (yi u 2 )T 1 (yi u 2 )}
(2 ) k/2
1/2
exp{ 12 (yi u1 )T 1 (yi u1 )}
(2 )
k/2
1
1
(2 ) k/2
a2
1 b 2 e r2
1/2
exp{ 12 (yi u 0 )T 1 (yi u 0 )}
a2
1 b2 e Tr2
,
a2
1 b 2 e 2 r2
,…,
a1
1 b1e 2 r1
, …,
a1
1 b1e Tr1
)
, …,
a0
1 b0 e Tr0
)
u1 = (
a1
1 b1e r1
,
u0 = (
a0
1 b 0 e r0
,
a0
1 b 0 e 2 r0
)
Estimation
n
2
i 1
j 0
log L(Θ p , Θ q | M, y ) log j|i f j ( yi )
log L(Θ p , Θ q | M , y )
n
2
f j ( yi ) Θjp|i
j|i Θ q f j ( yi )
2
2
j|i f j ( yi ) j 0 j|i f j ( yi )
i 1 j 0
j
0
1 j|i
2
log f j ( yi )
j|i f j ( yi ) j|i Θ p Θ q
i 1 j 0
j 0
n
2
j|i f j ( yi )
1 j|i
j|i
log f j ( yi )
i 1 j 0
j|i Θ p Θ q
n
2
The EM algorithm
E step
j|i
j|i f j (yi )
2
j 0
j |i f j (yi )
Calculate the posterior probability of QTL genotype j
for individual i that carries a known marker genotype
M step
L(Θ p , Θ q | y ) 0
Solve the log-likelihood equations
Iterations are made between the E and M steps
until convergence
EM continued
The likelihood function:
n
L() 2i f 2 ( zi ) 10i f10 ( zi ) 01i f 01 ( zi ) 0i f 0 ( zi )
i 1
f j ( zi )
uj (
1
(2 )T / 2
aj
1 bj e
rj
,
1/ 2
exp{ 12 ( zi log( u j )) ' 1 ( zi log( u j ))}
aj
1 bj e
2rj
,...,
aj
1 bj e
Trj
)
Statistical Derivations
M-step: update the parameters (see Ma et al. 2002, Genetics for details)
Testing QTL effect: Global test
• Instead of testing the mean difference at every time points for
different genotypes, we test the difference of the curve
parameters.
• The existence of QTL is tested by
• H0 means the three mean curves overlap and there is no QTL
effect.
• Likelihood ratio test with permutation to assess significance.
~
LR 2[log L() log L()]
where the notation “~” and “^” indicate parameters estimated
under the null and the alternative hypothesis, respectively.
Testing QTL effect: Regional test
• Regional test: to test at which time period [t1,t2] the
detect QTL triggers an effect, we can test the
difference of the area under the curve (AUC) for
different QTL genotype, i.e.,
| AUC | AUC |
t2
AA t1
H 0 : AUC
where
AUC |
t2
j t1
t2
t1
aj
rj
t2
Aa t1
aj
1 bje
rj t
t2
aa t1
dt j 1,2,3
[log( b j e
r j t2
) log( b j e j 1 )]
rt
• Permutation tests can be applied to assess statistical
significance.
Applications
• Several real examples are used to show the utility
of the functional mapping approach.
• Application I is about a poplar growth data set.
• Application II is about a mouse growth data set.
• Application III is about a rice tiller number
growth data set.
Application I: A Genetic Study
in Poplars
Parents AA aa
Genetic
design
F1
BC
Aa AA
AA
Aa
½
½
Stem diameter growth in poplar trees
g (t )
a
1 be rt
a:
Asymptotic growth
b:
Initial growth
r:
Relative growth rate
Ma, Casella & Wu,
Genetics 2002
Differences in growth across ages
Untransformed
Poplar
data
Log-transformed
Modeling the covariance structure
Stationary parametric approach
First-order autoregressive model (AR(1))
1
2
Σ
T 1
1
T 2
T 1
T 2
1
q = (,2)
Multivariate Box-Cox transformation to stabilize variance (Box and
Cox, 1964
Transform-both-side (TBS) technique to reserve the interpretability
of growth parameters (Carrol and Ruppert, 1984; Wu et al.,
2004). For a log transformation (i.e., =0),
Functional mapping incorporated
by logistic curves and AR(1) model
Results by FunMap
Results by Interval mapping
FunMap has higher
power to detect the
QTL than the
traditional interval
mapping method
does.
QTL
Ma, Casella & Wu,
Genetics 2002
Application II:
Mouse Genetic Study
Detecting Growth Genes
Data supplied by Dr. Cheverud at Washington University
Mouse Linkage Map
Body Mass Growth for Mouse
Parents AA aa
50
45
F1
Aa Aa
F2
AA Aa aa
¼ ½ ¼
40
35
Weight
30
25
20
15
10
5
0
1
2
3
4
5
6
7
8
Week
510 individuals measured
Over 10 weeks
9
10
Functional mapping
Genetic control of body mass growth in mice
Zhao, Ma, Cheverud & Wu,
Physiological Genomics
2004
Application III: functional mapping
of PCD QTL
• Rice tiller development is thought to be controlled by
genetic factors as well as environments.
• The development of tiller number growth undergoes a
process called programmed cell death (PCD).
Parents AA aa
Genetic
design
F1
DH
Aa
AA
aa
½
½
Joint model for the mean vector
• We developed a joint modeling approach with growth and
death phases are modeled by different functions.
• The growth phase is modeled by logistic growth curve to fit
the universal growth law .
• The dead phase is modeled by orthogonal Legendre function to
increase the fitting flexibility.
Cui et al. (2006) Physiological Genomics
QTL trajectory plot
Advantages of Functional Mapping
• Incorporate biological principles of growth and development
into genetic mapping, thus, increasing biological relevance of
QTL detection
• Provide a quantitative framework for hypothesis tests at the
interplay between gene action and developmental pattern
- When does a QTL turn on?
- When does a QTL turn off?
- What is the duration of genetic expression of a QTL?
- How does a growth QTL pleiotropically affect developmental events?
• The mean-covariance structures are modeled by parsimonious
parameters, increasing the precision, robustness and stability of
parameter estimation
Functional Mapping:
toward high-dimensional biology
• A new conceptual model for genetic
mapping of complex traits
• A systems approach for studying
sophisticated biological problems
• A framework for testing biological
hypotheses at the interplay among genetics,
development, physiology and biomedicine
Functional Mapping:
Simplicity from complexity
• Estimating fewer biologically meaningful
parameters that model the mean vector,
• Modeling the structure of the variance
matrix by developing powerful statistical
methods, leading to few parameters to be
estimated,
• The reduction of dimension increases the
power and precision of parameter
estimation