Download A neutrally charged object has equal numbers of electrons and

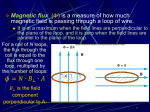
Charged Objects
A neutrally charged object has equal numbers of electrons and protons.
When an object becomes charged it either: gains electrons  becomes negatively charged.
 loses electrons  becomes positively charged.
NB electrons that are orbiting the nucleus of an atom are easily removed or accepted where protons that are
tightly bound up in the nucleus are not. Electrons are the agents of charge not protons.
Electric Fields 9.4.1.2 (iv), (vi)
An electric field is a region of influence in which a charged object will experience a force. All charged
objects will produce an electric field. Field lines can be used to represent electric field. These lines have the
following characteristics
 they never cross
 they leave surfaces at right angles
 the closeness of the lines indicate field strength. Close lines = greater field
 arrows indicate the field direction which is the direction of the force on a positive charge at that point
 The direction of the field in a curved field is a tangent to the curve at that particular point.
Field between charged parallel plates
Field between a point charge and a charged plate
Force on a Charge in an Electric field 9.4.1.3(iii)
The magnitude of a force on a charge in an electric field is described by the following equation :-
or
where E= electric field strength (NC-1)
F = force on charge (N),
q = magnitude of charge (C),
NB charge on an electron = -1.6 x 10-19C (data sheet)
charge on a proton = +1.6 x 10-19 C (data sheet)
A proton is paced in a field at q as shown above.
If it experiences a force of 9.0 x 10-19N.
Calculate the size of the electric field.
An electron is placed in an electric field at Q. If the
field is 2.5 NC-1, what is the force experience by
the electron?
Electric Field between parallel plates 9.4.1.2(vii)
The size of the field between charged parallel plates depends on the potential difference between the the plates and
the distance between them.
or
where E= electric field strength (Vm-1) or (NC-1)
V= potential difference between plates (V)
d= perpendicular distance between plates (m)
Force on a moving charge in a magnetic field 9.4.1.2 (iii), (v)
As well as experiencing a force in an electric field a charge will also experience a force in a magnetic field
as long as it is moving relative to the magnetic field. The size of this force is dependent on three quantities.
These are
 The size of the charge
 The size of the magnetic field
 The size of the velocity
Mathematically, this is described in the following equation:Where F= force on the charge (N)
q = size of the charge (C)
v = velocity of the charge through the field (ms-1)
= angle between velocity and the magnetic field
NB on angle between magnetic field and velocity
NB
If velocity is perpendicular to the field,
then the angle is 900 sin  = sin 90o = 1  force is a maximum.
If velocity is parallel to field,
then angle is zero  sin  = sin 00 = 0  no force is experienced
Direction of Force
The direction of the force experienced
by a moving charge in a magnetic field
can be determined using Flemmings
Left Hand Rule.
NB That the directions of the velocity,
magnetic field and the force a
experienced are all at 90 degrees to one
another.
For each of the following situations you should be able to calculate the magnitude and the initial direction on
the charge. Answers are in the table at bottom right.
Once inside the magnetic field the charge will change its velocity due to the force experienced; it will
accelerate. The speed will not change but the direction will. As the charge changes direction the force will
also change its direction so it is always be perpendicular to the velocity. As a result the charge will undergo
uniform circular motion where the magnetic force is providing the centripetal force required.
When in the field:Magnetic Force is providing the Centripetal Force
NB This algebra is important to understanding Thomson’s experiment
If the charge enters at an angle to the field as shown below, the charge will follow a helical path. below.
Cathode Ray Tubes – manipulating charged particles. 9.4.1.2(ii)
A cathode ray tube is a highly evacuated glass tube containing two electrodes. A high voltage applied across
the electrodes causes cathode rays, streams of negatively charged particles (electrons), to flow from the
cathode towards the anode, with little obstruction from the few remaining gas particles.
Structures built into or around the cathode ray tube allow the cathode rays to be manipulated. Further
electrodes can be built into the cathode ray tube to create an electric field to change the path of the cathode
rays. Magnetic fields can be applied to the cathode rays through the glass from outside the tube. Solid
objects can also be placed inside the tube to block the path of the rays.
Some of the variations of the cathode ray tube are
shown below – See Exp 1.2
Outline of Thomson’s Experiment 9.4.1.2(viii)
Step 1 Cathode rays were allowed to pass through the
apparatus the magnetic field was on and the electric field
was off. The rays were observed to follow a curved path
when passing through the magnetic field. This was due
to the magnetic force on the cathode rays. The radius
was measured and the magnetic field strength was
noted.
Step 2 Maintaining the same the magnetic field the
electric field was turned on and adjusted so that the
cathode ray beam travelled through both fields with zero
net deflection. At this point the magnetic force in one
direction was equal to the electric force in the other
direction.
Inconsistent behaviour of cathode rays – Charged Particles or Electromagnetic Waves 9.4.1.2 (i)
Applications of cathode ray tubes – CRO’s and TV’s (ix)