Download Entering and leaving group effects in Oh ligand substitutions

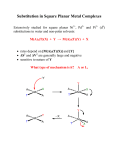
9B-1 Entering and leaving group effects in Oh ligand substitutions
Applies for reactions proceeding by Id mechanisms (i.e. 1st row metals with dn ≥ d2).
Don’t anticipate a large effect of the nature of the entering ligand (Y) on the rate of substitution.
e.g. [Ni(H2O)6]2+ + Y <––
––> [Ni(H2O)5Y]2+ + H2O
Table 26.6, p.987
But since G‡ is dependent on M-X bond weakening, do expect rate variations depending on the
nature of the leaving group (X). Has been studied exhaustively for Oh complexes of Co3+.
[Co(NH3)5X]2+ + H2O <––
––> [Co(NH3)5(H2O)]3+ + X–
• rate increases for X– = OH– < N3– ≈ NCS– < MeCO2– < Cl– < Br– < I– < NO3–
k ~ 10-9 s-1
k ~ 10-6 s-1
k ~ 10-5 s-1
k ~ 10-10 s-1
9B-2
Dissociative ligand substitutions:
linear free energy relationships
For these dissociative aquation reactions, there is a correlation between the rate of the reaction
and the strength of the M-X bond.
[Co(NH3)5X]2+ + H2O <––
––> [Co(NH3)5(H2O)]3+ + X–
If a plot of log k versus log K for a simple substitution reaction gives a straight line, it implies a
linear free energy relationship (LFER) exists for the reaction.
Linear free energy relationships
9B-3
[Co(NH3)5X]2+ + H2O ––> [Co(NH3)5(H2O)]3+ + X–
Fig 26.7, p.988
9B-4
Ancillary ligand effects in Oh ligand substitutions
The ligands that are not participating in the substitution reaction can also have some effect on
the rate of a dissociative or ID reaction.
e.g. the following reaction is much faster for L = NH3 than for L = H2O. Why?
[NiL5X]+ + H2O –––> [NiL5(H2O)]2+ + X–
Good sigma donors help to stabilize the lower C.N. in the Id transition state.
(Thus this observation supports a proposal that Id mechanism in effect)
9B-5
Ancillary ligand effects in Oh ligand substitutions
e.g. rates for the following reaction decrease as L = PPh3 > PPh2Me > PPhMe2.
– PR3
The reaction is faster with increasing size of ancillary ligands
The steric bulk of phosphines is described by Tolman’s “cone angle”
(Chem. Rev. 1977, 77, 313):
9B-6
Base-catalyzed hydrolysis
Generally we don’t expect to see rate dependence of an Id substitution mechanism on the
incoming ligand, Y. An exception is observed for cobalt(III) ammine complexes when Y is a good
base such as OH–.
[Co(NH3)5X]2+ + [OH]– ––> [Co(NH3)5(OH)]2+ + X–
kinetics show
rate = k[[Co(NH3)5X][OH–]
Normally this suggests an A or Ia mechanism….
BUT
The proposed mechanism includes pre-equilibrium step: initial deprotonation of an NH3 ligand
by OH–.
9B-7
Base-catalyzed hydrolysis
Ligand deprotonation generates a conjugate base of the starting complex
containing an amido ligand, NH2–.
The NH2- ligand stabilizes a lower (5-coordinate) transition state,
because it is both a good sigma donor and a good π-donor.
this accelerates rate-determining step: loss of Cl– ion
Reaction studies of 16O/18O isotope effects indicate that OH– in the product complex comes
from bulk H2O, not from OH–(aq)
9B-8
A brief comment on stereochemistry in Oh substitutions
In 26.4 there is a discussion of stereochemical outcomes for an Oh complex undergoing
substitution via a D mechanism, with a five-coordinate intermediate.
Fig 26.8, p.988
ability to rationalize product stereoisomer distributions with this argument relies on very short
intermediate lifetimes!
9B-9
Fluxional behaviour of 5-coordinate complexes
Recall that Trigonal bipyramidal and square pyramidal geometries are very close in energy.
TBP
Sq. Py.
e.g. [Fe(CO)5]
e.g. [Ni(CN)5]3–
In addition, the barrier to exchange between the two geometries is very low. This enables a
possible Berry pseudo-rotation if the 5-coordinate intermediate (previous page) is long-lived.
9B-10
Ligand substitution in square planar complexes
26.3
This discussion is based on exhaustive study of the substitution reactions of square planar Pt(II)
complexes, which normally proceed via A or Ia mechanisms.
The Pt(II) chemistry provides good examples of the important features of associative-type
mechanisms.
e.g. activation parameters:
Table 26.1, p.979
Ligand substitution in square planar complexes
9B-11
26.3
There is little (if any) dependence of rates of aquation of Pt-Cl bonds on complex charge:
[PtCl4]2–
kaq=
(x 105)
3.9
[Pt(NH3)Cl3]–
5.6
cis-[Pt(NH3)2Cl2]
2.5
trans-[Pt(NH3)2Cl2]
9.8
[Pt(NH3)3Cl]+
2.6
26.3
9B-12
Ligand substitution in square planar complexes: rate law
For the reaction
PtL3X + Y ––> PtL3Y + X
Rate = kY[Y][PtL3X] + kS[PtL3X]
There are two competing mechanisms:
26.3
9B-13 Ligand substitution in square planar complexes: rate law
26.3
If the reaction is performed using a large excess of Y (as well as solvent) the rate law simplifies to
Rate = kobs[PtL3X] where kobs = kY[Y] + kS
Experimentally:
(i) monitor disappearance of PtL3X over time to get a pseudo 1st order rate constant, kobs
(Slope of ln[PtL3X] vs t)
(ii) Repeat for different (excessively large) values of [Y]
(iii) Plot resulting kobs vs [Y] to get slope (kY) and intercept (kS)
Find kY and kS for different Y and S: indicates which of the two pathways dominates.
9B-14 Pt(II) substitutions: effects of incoming ligand and solvent
Huheey et al, 4th Ed.p.541
common intercept for all Y
Slope of plot depends on “nucleophile”(Y)
ky dominates for Y = softer ligands
i.e. for the soft metal Pt(II), soft bases make
good nucleophiles; stabilizes t.s. (strong M-Y
bond formation), lowers G‡
9B-15 Pt(II) substitutions: effects of incoming ligand and solvent
Huheey et al, 4th Ed.p.541
Intercept moves up or down depending on
how good a ligand the solvent is for Pt(II)
low rate dependence on [Y] does not mean
dissociative mechanism is in effect. Rather, the
solvent effect “masks” the rate dependence on
[Y].
Rate = kY[Y][PtL3X] + kS[PtL3X]
9B-16
Other effects consistent with A, Ia
An increase in the steric demands of Y or (ancillary) L can decrease the rate of substitution.
This is consistent with a mechanism involving increased C.N. or bond-making, at the transition
state
9B-17
Other effects consistent with A, Ia
the rates of substitution at square planar complexes tend to decrease down a triad.
e.g.
This may seem counter-intuitive, based on trends in
1. M-L bond strength – stronger for heavier metals
2. Size of M
9B-18
Changes in LFSE during ligand substitutions
For square planar complexes undergoing associative ligand substitution, there is no way to avoid
overall loss in LFSE at, or on the way to, the five coordinate intermediate, and the effect is more
pronounced as the d-orbital splitting (Δ) increases
Fig. 20.11, p.676
9B-19
Effects of the leaving group
Leaving group effects can be rationalized in part based on hard-soft comparisons:
X
NO3ClBrICN-
k (M-1s-1)
very fast
5.3·10-3
3.5·10-3
1.5·10-4
2.8·10-6
If X is a good leaving group, entering group (nucleophile) effects are relatively minor
If X is a poor leaving group, entering group (nucleophile) effects become more important
9B-20
The trans-effect
In substitutions at square planar Pt(II), we frequently see retention of stereochemistry:
The “trans effect”: the ligand in a square planar complex that becomes the leaving group (i.e.
departs most quickly) is determined by the nature of the ligand trans- to it.
Corollary: strong trans-effect ligands tend to facilitate the substitution of ligands trans to them.
eg. in these reactions, how do we predict which is the leaving group?
9B-21
The trans-effect
In the second step, there is a kinetic preference for the formation of the cis-product
Thus the Cl– trans to the other Cl– is more LABILE than Cl– trans to NH3.
Conclusion: Cl– has a higher trans effect than NH3
The kinetic trans-effect arises from both ground state (thermodynamic trans-influence)
and transition state effects.
• For Sq Pl Pt(II) complexes, typically see this order of trans-effect:
H2O ≈ [OH]– ≈ NH3 ≈ py < Cl–~Br– < I– ≈ [NO2]– < Ph– < Me– < PR3≈H–<<CO≈[CN]–≈C2H4
9B-22
The trans-effect: why?
Good π-acceptor ligands (e.g. C2H4, CN–, CO, PR3) offset increased e– density at the metal
centre in a trigonal bipyramidal, 5-coordinate transition state.
Requires coplanarity of three ligands (L2, X, Y) for shared π-bonding.
This by default makes the ligands (L1 and L3) that are cis to the trans-effect ligand in the ground
state and. axial in the transition state not involved in the substitution.
Fig. 26.5, p.981
9B-23
Trans influence
The kinetic trans-effect arises from both ground state (thermodynamic trans-influence)
and transition state effects. Ground state effects can be assessed experimentally, e.g. bond
lengths, IR, NMR
Ligands trans-to each other compete for electron density because both M-L bonds use the same
metal orbitals, e.g. dz2 or pz
See p. 831 in Ch.22, Box 22.8:
Very strong -donors (e.g. H– and alkyl– ligands) compete for orbital overlap at the metal with
the leaving group: this weakens the M-L bond in the ground state.
For comparable -donors (e.g. Cl– and NH3 ligands) the better π-donor is the higher influence
(and effect) ligand.
Trans influence
9B-24
d (Pt-Cl),
Å (= 10-10m)
231.6
232.7 (t)
230.5 (c)
X
CNIBrCl-
237
ν(Pt-H), cm-1
2041
2156
2178
2183
242
9B-25
Exploiting the trans-effect in synthesis
If the substitution reaction is under “kinetic control”, the trans-effect can be used to design
substitution products of specific stereochemistries.
The classic example is making either cis- or trans-[PtCl2(NH3)2], based on Cl– being a higher
trans-effect ligand than NH3.