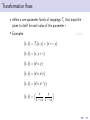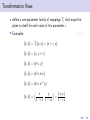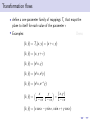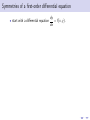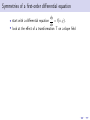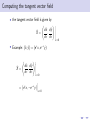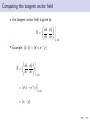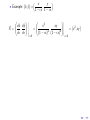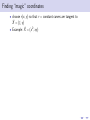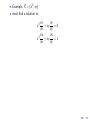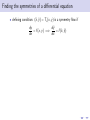Download Using symmetry to solve differential equations

Using symmetry to solve differential equations
Martin Jackson
Mathematics and Computer Science, University of Puget Sound
March 6, 2012
Outline
1 “Magic” coordinates
Outline
1 “Magic” coordinates
2 Symmetries of a differential equation
Outline
1 “Magic” coordinates
2 Symmetries of a differential equation
3 Using a symmetry to find “magic” coordinates
Outline
1 “Magic” coordinates
2 Symmetries of a differential equation
3 Using a symmetry to find “magic” coordinates
4 Finding symmetries of a differential equation
Outline
1 “Magic” coordinates
2 Symmetries of a differential equation
3 Using a symmetry to find “magic” coordinates
4 Finding symmetries of a differential equation
5 Topics for another time
“Magic” coordinates
“Magic” coordinates
• start with a differential equation
dy
= f (x, y )
dx
“Magic” coordinates
• start with a differential equation
dy
= f (x, y )
dx
2
1
y
0
-1
-2
0
1
2
x
3
4
dy
= f (x, y )
dx
“Magic” coordinates
dy
= f (x, y )
dx
ds
• goal: find new variables to get
= g (r )
dr
dy
= f (x, y )
dx
• start with a differential equation
2
1
y
0
-1
-2
0
1
2
x
3
4
“Magic” coordinates
dy
= f (x, y )
dx
ds
• goal: find new variables to get
= g (r )
dr
ds
dy
= g (r )
= f (x, y )
dr
dx
• start with a differential equation
y
2
0
1
-1
s
0
-1
-2
-3
-2
-4
0
1
2
x
3
4
-2
-1
0
r
1
2
• Example:
dy
=y
dx
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
2
1
y
0
-1
-2
-2
-1
0
x
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
r
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
• obvious choice: r = y and s = x
-1
0
r
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
• obvious choice: r = y and s = x
• change coordinates:
-1
0
r
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
-1
0
r
• obvious choice: r = y and s = x
• change coordinates:
ds
dr
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
-1
0
r
• obvious choice: r = y and s = x
• change coordinates:
ds
dx
=
dr
dy
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
-1
0
r
• obvious choice: r = y and s = x
• change coordinates:
ds
dx
1
=
=
dr
dy
dy /dx
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
-1
x
0
r
• obvious choice: r = y and s = x
• change coordinates:
ds
dx
1
1
=
=
=
dr
dy
dy /dx
y
1
2
dy
=y
dx
• find new coordinates (r , s) to simplify problem
• Example:
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
-1
0
r
• obvious choice: r = y and s = x
• change coordinates:
ds
dx
1
1
1
=
=
= =
dr
dy
dy /dx
y
r
1
2
Using “magic” coordinates
Using “magic” coordinates
• change coordinates:
ds
1
dy
= y =⇒
=
dx
dr
r
Using “magic” coordinates
• change coordinates:
ds
1
dy
= y =⇒
=
dx
dr
r
• integrate:
Z
s=
1
dr = ln r + C
r
Using “magic” coordinates
• change coordinates:
ds
1
dy
= y =⇒
=
dx
dr
r
• integrate:
Z
s=
1
dr = ln r + C
r
• change back:
x = ln y + C
Using “magic” coordinates
• change coordinates:
ds
1
dy
= y =⇒
=
dx
dr
r
• integrate:
Z
s=
1
dr = ln r + C
r
• change back:
x = ln y + C
• solve:
y = Ce x
Another example of “magic” coordinates
Another example of “magic” coordinates
• Example:
dy
y
y2
= + 3
dx
x
x
Another example of “magic” coordinates
• Example:
dy
y
y2
= + 3
dx
x
x
2
1
y
0
-1
-2
0
1
2
x
3
4
Another example of “magic” coordinates
dy
y
y2
= + 3
dx
x
x
y
1
• a not-so-obvious choice: r =
and s = −
x
x
• Example:
2
1
y
0
-1
-2
0
1
2
x
3
4
Another example of “magic” coordinates
dy
y
y2
= + 3
dx
x
x
y
1
• a not-so-obvious choice: r =
and s = −
x
x
• change coordinates:
• Example:
d(− x1 )
ds
1
=
= ... = 2
y
dr
d( x )
r
2
1
y
0
-1
-2
0
1
2
x
3
4
Another example of “magic” coordinates
dy
y
y2
= + 3
dx
x
x
y
1
• a not-so-obvious choice: r =
and s = −
x
x
• change coordinates:
• Example:
d(− x1 )
ds
1
=
= ... = 2
y
dr
d( x )
r
y
2
0
1
-1
s
0
-1
-2
-3
-2
-4
0
1
2
x
3
4
-2
-1
0
r
1
2
• change coordinates:
dy
y
y2
1
ds
= + 3 =⇒
= 2
dx
x
x
dr
r
• change coordinates:
dy
y
y2
1
ds
= + 3 =⇒
= 2
dx
x
x
dr
r
• integrate:
Z
s=
1
1
dr = − + C
2
r
r
• change coordinates:
dy
y
y2
1
ds
= + 3 =⇒
= 2
dx
x
x
dr
r
• integrate:
Z
s=
1
1
dr = − + C
2
r
r
• change back:
−
1
x
=− +C
x
y
• change coordinates:
dy
y
y2
1
ds
= + 3 =⇒
= 2
dx
x
x
dr
r
• integrate:
Z
1
1
dr = − + C
2
r
r
s=
• change back:
−
1
x
=− +C
x
y
• solve:
y=
x2
1 + Cx
• change coordinates:
dy
y
y2
1
ds
= + 3 =⇒
= 2
dx
x
x
dr
r
• integrate:
Z
1
1
dr = − + C
2
r
r
s=
• change back:
−
1
x
=− +C
x
y
• solve:
y=
x2
1 + Cx
• Question: how do we come up with r =
y
1
and s = − ?
x
x
• change coordinates:
dy
y
y2
1
ds
= + 3 =⇒
= 2
dx
x
x
dr
r
• integrate:
Z
1
1
dr = − + C
2
r
r
s=
• change back:
−
1
x
=− +C
x
y
• solve:
y=
x2
1 + Cx
• Question: how do we come up with r =
• Answer: symmetry!
y
1
and s = − ?
x
x
Transforming the plane
Transforming the plane
• define a mapping T of the plane to itself
Transforming the plane
• define a mapping T of the plane to itself
• Example: reflection across the y -axis:
Transforming the plane
• define a mapping T of the plane to itself
• Example: reflection across the y -axis:
y
Hx,yL
x
Transforming the plane
• define a mapping T of the plane to itself
• Example: reflection across the y -axis:
y
` `
Hx ,y L
Hx,yL
x
Transforming the plane
• define a mapping T of the plane to itself
• Example: reflection across the y -axis:
y
` `
Hx ,y L
Hx,yL
x
• denote this
(x̂, ŷ ) = T (x, y ) = (−x, y )
Transformation flows
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
(x̂, ŷ ) = (e x, y )
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
(x̂, ŷ ) = (e x, y )
(x̂, ŷ ) = (e x, e y )
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
(x̂, ŷ ) = (e x, y )
(x̂, ŷ ) = (e x, e y )
(x̂, ŷ ) = (e x, e − y )
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
(x̂, ŷ ) = (e x, y )
(x̂, ŷ ) = (e x, e y )
(x̂, ŷ ) = (e x, e − y )
(x̂, ŷ ) =
x
y ,
1 − x 1 − x
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
(x̂, ŷ ) = (e x, y )
(x̂, ŷ ) = (e x, e y )
(x̂, ŷ ) = (e x, e − y )
(x̂, ŷ ) =
x
y (x, y )
,
=
1 − x 1 − x
1 − x
Transformation flows
• define a one-parameter family of mappings T that maps the
plane to itself for each value of the parameter • Examples:
Demo
(x̂, ŷ ) = T (x, y ) = (x + , y )
(x̂, ŷ ) = (x, y + )
(x̂, ŷ ) = (e x, y )
(x̂, ŷ ) = (e x, e y )
(x̂, ŷ ) = (e x, e − y )
(x̂, ŷ ) =
x
y (x, y )
,
=
1 − x 1 − x
1 − x
(x̂, ŷ ) = (x cos − y sin , x sin + y cos )
Lie group structure
• each of these transformation flows has certain algebraic
properties:
T0 = Id
T ◦ Tδ = T+δ
T−1 = T−
Lie group structure
• each of these transformation flows has certain algebraic
properties:
T0 = Id
T ◦ Tδ = T+δ
T−1 = T−
• so each of these is a group under composition
Lie group structure
• each of these transformation flows has certain algebraic
properties:
T0 = Id
T ◦ Tδ = T+δ
T−1 = T−
• so each of these is a group under composition
• each flow is also “nice” as a function of Lie group structure
• each of these transformation flows has certain algebraic
properties:
T0 = Id
T ◦ Tδ = T+δ
T−1 = T−
• so each of these is a group under composition
• each flow is also “nice” as a function of • so each is a one-parameter group of transformations that is
“nice” as a function of Lie group structure
• each of these transformation flows has certain algebraic
properties:
T0 = Id
T ◦ Tδ = T+δ
T−1 = T−
• so each of these is a group under composition
• each flow is also “nice” as a function of • so each is a one-parameter group of transformations that is
“nice” as a function of • these are called one-parameter Lie groups
Lie group structure
• each of these transformation flows has certain algebraic
properties:
T0 = Id
T ◦ Tδ = T+δ
T−1 = T−
• so each of these is a group under composition
• each flow is also “nice” as a function of • so each is a one-parameter group of transformations that is
“nice” as a function of • these are called one-parameter Lie groups
• now ready to define symmetries of geometric objects
Symmetries of a curve
• look at the effect of a transformation flow on a geometric
object
Symmetries of a curve
• look at the effect of a transformation flow on a geometric
object
• Example: What happens to the unit circle under each of the
previous transformation flows?
Demo
Symmetries of a curve
• look at the effect of a transformation flow on a geometric
object
• Example: What happens to the unit circle under each of the
previous transformation flows?
Demo
• under most of them, the circle is not mapped to itself
Symmetries of a curve
• look at the effect of a transformation flow on a geometric
object
• Example: What happens to the unit circle under each of the
previous transformation flows?
Demo
• under most of them, the circle is not mapped to itself
• the circle is mapped to itself for rotation through any
angle Symmetries of a curve
• look at the effect of a transformation flow on a geometric
object
• Example: What happens to the unit circle under each of the
previous transformation flows?
Demo
• under most of them, the circle is not mapped to itself
• the circle is mapped to itself for rotation through any
angle • the circle has a symmetry for each angle so the circle
has a one-parameter symmetry flow (in this case, a
one-parameter Lie symmetry)
Symmetries of a curve
• look at the effect of a transformation flow on a geometric
object
• Example: What happens to the unit circle under each of the
previous transformation flows?
Demo
• under most of them, the circle is not mapped to itself
• the circle is mapped to itself for rotation through any
angle • the circle has a symmetry for each angle so the circle
has a one-parameter symmetry flow (in this case, a
one-parameter Lie symmetry)
• in general, a geometric object in the plane has a symmetry
flow (or a Lie symmetry) if there is a “nice” transformation
flow of the plane that maps that object to itself
First-order differential equations as geometric objects
First-order differential equations as geometric objects
• geometric view of a first-order ODE as a slope field.
First-order differential equations as geometric objects
• geometric view of a first-order ODE as a slope field.
• Examples:
First-order differential equations as geometric objects
• geometric view of a first-order ODE as a slope field.
• Examples:
dy
=y
dx
2
1
y
0
-1
-2
-2
-1
0
x
1
2
First-order differential equations as geometric objects
• geometric view of a first-order ODE as a slope field.
• Examples:
y
y2
dy
= + 3
dx
x
x
dy
=y
dx
y
2
2
1
1
0
y
-1
0
-1
-2
-2
-2
-1
0
x
1
2
0
1
2
x
3
4
First-order differential equations as geometric objects
• geometric view of a first-order ODE as a slope field.
• Examples:
y
y2
dy
= + 3
dx
x
x
dy
=y
dx
y
2
2
1
1
0
y
-1
0
-1
-2
-2
-2
-1
0
x
1
2
0
1
2
3
4
x
• to understand how a slope field transforms, first look at how
slopes transform
Effect of a transformation on slopes
Effect of a transformation on slopes
• Example: translation in x
Effect of a transformation on slopes
• Example: translation in x
•
each point is mapped by (x̂, ŷ ) = (x + , y )
Effect of a transformation on slopes
• Example: translation in x
•
•
each point is mapped by (x̂, ŷ ) = (x + , y )
each tangent line segment at (x, y ) is mapped to a
tangent line segment at (x̂, ŷ )
Effect of a transformation on slopes
• Example: translation in x
•
•
each point is mapped by (x̂, ŷ ) = (x + , y )
each tangent line segment at (x, y ) is mapped to a
tangent line segment at (x̂, ŷ )
y
m
Hx,yL
x
Effect of a transformation on slopes
• Example: translation in x
•
•
each point is mapped by (x̂, ŷ ) = (x + , y )
each tangent line segment at (x, y ) is mapped to a
tangent line segment at (x̂, ŷ )
y
`
m
m
Hx,yL
` `
Hx ,y L
x
Effect of a transformation on slopes
• Example: translation in x
•
•
each point is mapped by (x̂, ŷ ) = (x + , y )
each tangent line segment at (x, y ) is mapped to a
tangent line segment at (x̂, ŷ )
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
each transformed tangent line segment has slope m̂ that
is the same as the original slope m so
(x̂, ŷ , m̂) = T (x, y , m) = (x + , y , m)
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
m
Hx,yL
x
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
m̂ =
ˆ
rise
run
ˆ
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
m̂ =
ˆ
rise
rise
= run
ˆ
e run
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
m̂ =
ˆ
rise
rise
rise
= = e −
run
ˆ
e run
run
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
m̂ =
ˆ
rise
rise
rise
= = e −
= e − m
run
ˆ
e run
run
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
m̂ =
•
so
ˆ
rise
rise
rise
= = e −
= e − m
run
ˆ
e run
run
(x̂, ŷ , m̂) = T (x, y , m) = (e x, y , e − m)
• Example: scaling in x: (x̂, ŷ ) = T (x, y ) = (e x, y )
•
tangent line segments will be scaled in the x-direction
y
`
m
m
Hx,yL
` `
Hx ,y L
x
•
scaling in x will scale run and have no effect on rise so
m̂ =
•
so
ˆ
rise
rise
rise
= = e −
= e − m
run
ˆ
e run
run
(x̂, ŷ , m̂) = T (x, y , m) = (e x, y , e − m)
Demo
Symmetries of a first-order differential equation
Symmetries of a first-order differential equation
• start with a differential equation
dy
= f (x, y ).
dx
Symmetries of a first-order differential equation
dy
= f (x, y ).
dx
• look at the effect of a transformation T on a slope field
• start with a differential equation
Symmetries of a first-order differential equation
dy
= f (x, y ).
dx
• look at the effect of a transformation T on a slope field
dy
• Example:
= y under reflection across the x-axis
dx
• start with a differential equation
Symmetries of a first-order differential equation
dy
= f (x, y ).
dx
• look at the effect of a transformation T on a slope field
dy
• Example:
= y under reflection across the x-axis
dx
• start with a differential equation
2
1
y
0
-1
-2
-2
-1
0
x
1
2
Symmetries of a first-order differential equation
dy
= f (x, y ).
dx
• look at the effect of a transformation T on a slope field
dy
• Example:
= y under reflection across the x-axis
dx
• start with a differential equation
y
2
2
1
1
`
y
0
0
-1
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
`
x
1
2
Symmetries of a first-order differential equation
dy
= f (x, y ).
dx
• look at the effect of a transformation T on a slope field
dy
• Example:
= y under reflection across the x-axis
dx
• start with a differential equation
y
2
2
1
1
`
y
0
0
-1
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
`
x
1
2
• T is a symmetry of the differential equation if the slope field
maps to itself (so each solution is mapped to a solution)
• our interest is in symmetry under a transformation flow
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
• our interest is in symmetry under a transformation flow
• Example: explore
•
dy
= y under various transformation flows
dx
Demo
translation in x:
• our interest is in symmetry under a transformation flow
• Example: explore
•
•
dy
= y under various transformation flows
dx
Demo
translation in x:
scaling in x:
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x:
scaling in x:
• translation in y :
•
•
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x:
scaling in x:
• translation in y :
• scaling in y :
•
•
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
• translation in y :
• scaling in y :
•
•
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y :
• scaling in y :
•
•
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
•
•
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• Example: explore
flows
y
y2
dy
= + 3 under various transformation
dx
x
x
Demo
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• Example: explore
flows
•
scaling in y :
y
y2
dy
= + 3 under various transformation
dx
x
x
Demo
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• Example: explore
flows
y
y2
dy
= + 3 under various transformation
dx
x
x
Demo
•
scaling in y :
•
projective transformation T (x, y ) =
(x, y )
:
1 − x
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• Example: explore
flows
y
y2
dy
= + 3 under various transformation
dx
x
x
Demo
•
scaling in y : not a symmetry flow
•
projective transformation T (x, y ) =
(x, y )
:
1 − x
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• Example: explore
flows
y
y2
dy
= + 3 under various transformation
dx
x
x
Demo
•
scaling in y : not a symmetry flow
•
projective transformation T (x, y ) =
(x, y ) a symmetry
:
flow
1 − x
• our interest is in symmetry under a transformation flow
• Example: explore
dy
= y under various transformation flows
dx
Demo
translation in x: a symmetry flow
scaling in x:
not a symmetry flow
• translation in y : not a symmetry flow
• scaling in y :
a symmetry flow
•
•
• Example: explore
flows
•
y
y2
dy
= + 3 under various transformation
dx
x
x
Demo
scaling in y : not a symmetry flow
(x, y ) a symmetry
:
flow
1 − x
• before working with symmetries of a differential equation, look
at a convenient way to picture a transformation flow
•
projective transformation T (x, y ) =
Visualizing a transformation flow
Visualizing a transformation flow
• have looked at how a grid of points moves
Visualizing a transformation flow
• have looked at how a grid of points moves
• can also look at paths traced out by points
Visualizing a transformation flow
• have looked at how a grid of points moves
• can also look at paths traced out by points
• Example: (x̂, ŷ ) = (e x, e − y )
Visualizing a transformation flow
• have looked at how a grid of points moves
• can also look at paths traced out by points
• Example: (x̂, ŷ ) = (e x, e − y )
2
1
y
0
-1
-2
-2
-1
0
x
1
2
Visualizing a transformation flow
• have looked at how a grid of points moves
• can also look at paths traced out by points
• Example: (x̂, ŷ ) = (e x, e − y )
2
2
1
y
1
y
0
0
-1
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
x
1
2
Visualizing a transformation flow
• have looked at how a grid of points moves
• can also look at paths traced out by points
• Example: (x̂, ŷ ) = (e x, e − y )
2
2
1
y
1
y
0
0
-1
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
~ = (ξ, η)
• denote the tangent vector field X
0
x
1
2
Computing the tangent vector field
Computing the tangent vector field
• the tangent vector field is given by
~ =
X
d x̂ d ŷ
,
d d
!
=0
Computing the tangent vector field
• the tangent vector field is given by
d x̂ d ŷ
,
d d
~ =
X
• Example: (x̂, ŷ ) = (e x, e
−
y)
!
=0
Computing the tangent vector field
• the tangent vector field is given by
d x̂ d ŷ
,
d d
~ =
X
• Example: (x̂, ŷ ) = (e x, e
~ =
X
d x̂ d ŷ
,
d d
!
=0
−
y)
!
=0
Computing the tangent vector field
• the tangent vector field is given by
d x̂ d ŷ
,
d d
~ =
X
• Example: (x̂, ŷ ) = (e x, e
~ =
X
d x̂ d ŷ
,
d d
−
!
=0
= e x, −e − y =0
y)
!
=0
Computing the tangent vector field
• the tangent vector field is given by
d x̂ d ŷ
,
d d
~ =
X
• Example: (x̂, ŷ ) = (e x, e
~ =
X
d x̂ d ŷ
,
d d
!
=0
= e x, −e − y = (x, −y )
−
=0
y)
!
=0
Computing the tangent vector field
• the tangent vector field is given by
d x̂ d ŷ
,
d d
~ =
X
• Example: (x̂, ŷ ) = (e x, e
−
!
=0
y)
2
~ =
X
!
d x̂ d ŷ ,
d d 1
=0
= e x, −e − y y
0
=0
-1
= (x, −y )
-2
-2
-1
0
x
1
2
• Example: (x̂, ŷ ) =
x
y ,
1 − x 1 − x
• Example: (x̂, ŷ ) =
~ =
X
d x̂ d ŷ
,
d d
!
=0
x
y ,
1 − x 1 − x
• Example: (x̂, ŷ ) =
~ =
X
d x̂ d ŷ
,
d d
!
=0
x
y ,
1 − x 1 − x
=
xy
x2
,
2
(1 − x) (1 − x)2
!
=0
• Example: (x̂, ŷ ) =
~ =
X
d x̂ d ŷ
,
d d
!
=0
x
y ,
1 − x 1 − x
=
xy
x2
,
2
(1 − x) (1 − x)2
!
=0
= x 2 , xy
• Example: (x̂, ŷ ) =
~ =
X
d x̂ d ŷ
,
d d
!
x
y ,
1 − x 1 − x
=
=0
xy
x2
,
2
(1 − x) (1 − x)2
!
=0
2
1
y
0
-1
-2
-2
-1
0
x
1
2
= x 2 , xy
• a few more examples of tangent vector fields:
• a few more examples of tangent vector fields:
Scaling in x
(x̂, ŷ ) = (e x, y )
~ = (x, 0)
X
2
1
y
0
-1
-2
-2
-1
0
x
1
2
• a few more examples of tangent vector fields:
Rotation
(x̂, ŷ ) = (x cos − y sin , x sin + y cos )
~ = (−y , x)
X
Scaling in x
(x̂, ŷ ) = (e x, y )
~ = (x, 0)
X
y
2
2
1
1
y
0
0
-1
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
x
1
2
Using a symmetry to solve the differential equation
Using a symmetry to solve the differential equation
• find coordinates (r , s) in which the symmetry field is vertical
and uniform
Using a symmetry to solve the differential equation
• find coordinates (r , s) in which the symmetry field is vertical
and uniform
~ = (x 2 , xy )
X
2
1
y
0
-1
-2
-2
-1
0
x
1
2
Using a symmetry to solve the differential equation
• find coordinates (r , s) in which the symmetry field is vertical
and uniform
~ = (x 2 , xy )
X
y
~ = (0, 1)
X
2
2
1
1
0
s
-1
0
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
r
1
2
Using a symmetry to solve the differential equation
• find coordinates (r , s) in which the symmetry field is vertical
and uniform
~ = (x 2 , xy )
X
y
~ = (0, 1)
X
2
2
1
1
0
s
-1
0
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
r
1
2
• in the new coordinates, differential equation reduces to an
antiderivative problem since symmetry maps solutions to
solutions by translation in the dependent variable
~ = (1, 0)
• Example: translation in x: X
~ = (1, 0)
• Example: translation in x: X
~ = (1, 0)
X
2
1
y
0
-1
-2
-2
-1
0
x
1
2
~ = (1, 0)
• Example: translation in x: X
• from the geometry, can see that choosing r = y , s = x works
~ = (1, 0)
X
2
1
y
0
-1
-2
-2
-1
0
x
1
2
~ = (1, 0)
• Example: translation in x: X
• from the geometry, can see that choosing r = y , s = x works
~ = (0, 1)
X
~ = (1, 0)
X
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
r
1
2
~ = (1, 0)
• Example: translation in x: X
• from the geometry, can see that choosing r = y , s = x works
~ = (0, 1)
X
~ = (1, 0)
X
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
• this is a symmetry flow for
dy
=y
dx
-1
0
r
1
2
~ = (1, 0)
• Example: translation in x: X
• from the geometry, can see that choosing r = y , s = x works
~ = (0, 1)
X
~ = (1, 0)
X
y
2
2
1
1
s
0
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
• this is a symmetry flow for
-1
0
r
1
2
dy
=y
dx
• in these “magic coordinates”, this ODE becomes
ds
1
=
dr
r
~ = (0, y )
• Example: scaling in y : X
~ = (0, y )
• Example: scaling in y : X
~ = (0, y )
X
2
1
y
0
-1
-2
-2
-1
0
x
1
2
~ = (0, y )
• Example: scaling in y : X
• from the geometry, see that r = x and s is some function of
y ; a choice that works is s = ln y
~ = (0, y )
X
2
1
y
0
-1
-2
-2
-1
0
x
1
2
~ = (0, y )
• Example: scaling in y : X
• from the geometry, see that r = x and s is some function of
y ; a choice that works is s = ln y
~ = (0, 1)
X
~ = (0, y )
X
y
2
2
1
1
0
s
-1
0
-1
-2
-2
-2
-1
0
x
1
2
-2
-1
0
r
1
2
~ = (0, y )
• Example: scaling in y : X
• from the geometry, see that r = x and s is some function of
y ; a choice that works is s = ln y
~ = (0, 1)
X
~ = (0, y )
X
y
2
2
1
1
0
s
-1
0
-1
-2
-2
-2
-1
0
1
2
-2
x
-1
0
r
1
2
dy
= y so can now transform
dx
the differential equation to the new coordinates
• this is also a symmetry flow for
Finding “magic” coordinates
• choose r (x, y ) so that r = constant curves are tangent to
~ = (ξ, η)
X
Finding “magic” coordinates
• choose r (x, y ) so that r = constant curves are tangent to
~ = (ξ, η)
X
~ = (x 2 , xy )
• Example: X
Finding “magic” coordinates
• choose r (x, y ) so that r = constant curves are tangent to
~ = (ξ, η)
X
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
Finding “magic” coordinates
• choose r (x, y ) so that r = constant curves are tangent to
~ = (ξ, η)
X
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
Finding “magic” coordinates
• choose r (x, y ) so that r = constant curves are tangent to
~ = (ξ, η)
X
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
• equivalent to choosing r (x, y ) so that the derivative in the
~ is 0:
direction of X
Finding “magic” coordinates
• choose r (x, y ) so that r = constant curves are tangent to
~ = (ξ, η)
X
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
• equivalent to choosing r (x, y ) so that the derivative in the
~ is 0:
direction of X
~ · ∇r
~ = ξ ∂r + η ∂r = 0
X
∂x
∂y
• choose s(x, y ) so that s = constant curves are nowhere
tangent to r = constant curves and the derivative in the
~ is uniform:
direction of X
~ · ∇s
~ = ξ ∂s + η ∂s = 1
X
∂x
∂y
• choose s(x, y ) so that s = constant curves are nowhere
tangent to r = constant curves and the derivative in the
~ is uniform:
direction of X
~ · ∇s
~ = ξ ∂s + η ∂s = 1
X
∂x
∂y
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
• choose s(x, y ) so that s = constant curves are nowhere
tangent to r = constant curves and the derivative in the
~ is uniform:
direction of X
~ · ∇s
~ = ξ ∂s + η ∂s = 1
X
∂x
∂y
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
• choose s(x, y ) so that s = constant curves are nowhere
tangent to r = constant curves and the derivative in the
~ is uniform:
direction of X
~ · ∇s
~ = ξ ∂s + η ∂s = 1
X
∂x
∂y
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
• choose s(x, y ) so that s = constant curves are nowhere
tangent to r = constant curves and the derivative in the
~ is uniform:
direction of X
~ · ∇s
~ = ξ ∂s + η ∂s = 1
X
∂x
∂y
~ = (x 2 , xy )
• Example: X
2
1
y
0
-1
-2
0
1
2
x
3
4
• looks intimidating but not so bad in practice since need only a
specific solution rather than the general solution
~ = (x 2 , xy )
• Example: X
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
=
2
x
xy
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
=
=⇒
=
2
x
xy
x
y
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
y
=
=⇒
=
=⇒
= constant
2
x
xy
x
y
x
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
y
y
=
=⇒
=
=⇒
= constant so r = works
2
x
xy
x
y
x
x
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
y
y
=
=⇒
=
=⇒
= constant so r = works
2
x
xy
x
y
x
x
• solve bottom equation by looking for s depending only on x so
x2
∂s
+ xy · 0 = 1
∂x
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
y
y
=
=⇒
=
=⇒
= constant so r = works
2
x
xy
x
y
x
x
• solve bottom equation by looking for s depending only on x so
x2
∂s
∂s
1
+ xy · 0 = 1 =⇒
= 2
∂x
∂x
x
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
y
y
=
=⇒
=
=⇒
= constant so r = works
2
x
xy
x
y
x
x
• solve bottom equation by looking for s depending only on x so
x2
∂s
∂s
1
1
+ xy · 0 = 1 =⇒
= 2 =⇒ s = −
∂x
∂x
x
x
~ = (x 2 , xy )
• Example: X
• must find a solution to
∂r
∂r
+ xy
=0
∂x
∂y
∂s
∂s
x2
+ xy
=1
∂x
∂y
x2
• top equation:r is constant along curves given by
dx
dy
dx
dy
y
y
=
=⇒
=
=⇒
= constant so r = works
2
x
xy
x
y
x
x
• solve bottom equation by looking for s depending only on x so
x2
∂s
∂s
1
1
+ xy · 0 = 1 =⇒
= 2 =⇒ s = −
∂x
∂x
x
x
• these are the “magic” coordinates we used at the start
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
• for that symmetry flow, find new coordinates r and s so that
~ = (0, 1)
the tangent vector field is X
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
• for that symmetry flow, find new coordinates r and s so that
~ = (0, 1)
the tangent vector field is X
• in the new coordinates, slopes can vary only in r and not in s
since translation in s maps slope field to slope field
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
• for that symmetry flow, find new coordinates r and s so that
~ = (0, 1)
the tangent vector field is X
• in the new coordinates, slopes can vary only in r and not in s
since translation in s maps slope field to slope field
• thus, in the new coordinates, the differential equation has the
form
ds
= g (r )
dr
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
• for that symmetry flow, find new coordinates r and s so that
~ = (0, 1)
the tangent vector field is X
• in the new coordinates, slopes can vary only in r and not in s
since translation in s maps slope field to slope field
• thus, in the new coordinates, the differential equation has the
ds
= g (r )
dr
• integrate!
form
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
• for that symmetry flow, find new coordinates r and s so that
~ = (0, 1)
the tangent vector field is X
• in the new coordinates, slopes can vary only in r and not in s
since translation in s maps slope field to slope field
• thus, in the new coordinates, the differential equation has the
ds
= g (r )
dr
• integrate!
form
• change back to the original coordinates
Review the general plan
• start with a differential equation in the form
meaning slopes can vary in both x and y
dy
= f (x, y )
dx
• find a symmetry flow for the differential equation with tangent
~ = (ξ, η)
vector field X
Wait a minute, how do we do that!?
• for that symmetry flow, find new coordinates r and s so that
~ = (0, 1)
the tangent vector field is X
• in the new coordinates, slopes can vary only in r and not in s
since translation in s maps slope field to slope field
• thus, in the new coordinates, the differential equation has the
ds
= g (r )
dr
• integrate!
form
• change back to the original coordinates
Finding the symmetries of a differential equation
Finding the symmetries of a differential equation
• defining condition: (x̂, ŷ ) = T (x, y ) is a symmetry flow if
dy
d ŷ
= f (x, y ) =⇒
= f (x̂, ŷ )
dx
d x̂
Finding the symmetries of a differential equation
• defining condition: (x̂, ŷ ) = T (x, y ) is a symmetry flow if
dy
d ŷ
= f (x, y ) =⇒
= f (x̂, ŷ )
dx
d x̂
~ = (ξ, η) by
• strategy: determine the tangent vector field X
linearizing the defining condition
Finding the symmetries of a differential equation
• defining condition: (x̂, ŷ ) = T (x, y ) is a symmetry flow if
dy
d ŷ
= f (x, y ) =⇒
= f (x̂, ŷ )
dx
d x̂
~ = (ξ, η) by
• strategy: determine the tangent vector field X
linearizing the defining condition
• start with
(x̂, ŷ ) = (x, y ) + (ξ, η) + higher-order terms to be ignored
Finding the symmetries of a differential equation
• defining condition: (x̂, ŷ ) = T (x, y ) is a symmetry flow if
dy
d ŷ
= f (x, y ) =⇒
= f (x̂, ŷ )
dx
d x̂
~ = (ξ, η) by
• strategy: determine the tangent vector field X
linearizing the defining condition
• start with
(x̂, ŷ ) = (x, y ) + (ξ, η) + higher-order terms to be ignored
• substitute into defining condition:
d(y + η)
= f (x + ξ, y + η)
d(x + ξ)
Finding the symmetries of a differential equation
• defining condition: (x̂, ŷ ) = T (x, y ) is a symmetry flow if
dy
d ŷ
= f (x, y ) =⇒
= f (x̂, ŷ )
dx
d x̂
~ = (ξ, η) by
• strategy: determine the tangent vector field X
linearizing the defining condition
• start with
(x̂, ŷ ) = (x, y ) + (ξ, η) + higher-order terms to be ignored
• substitute into defining condition:
d(y + η)
= f (x + ξ, y + η)
d(x + ξ)
• after the dust settles:
∂η
∂η
∂ξ ∂f
∂f
∂ξ
+f
−
=
ξ+
η
−f2
∂x
∂y
∂x
∂y
∂x
∂y
Finding the symmetries of a differential equation
• defining condition: (x̂, ŷ ) = T (x, y ) is a symmetry flow if
dy
d ŷ
= f (x, y ) =⇒
= f (x̂, ŷ )
dx
d x̂
~ = (ξ, η) by
• strategy: determine the tangent vector field X
linearizing the defining condition
• start with
(x̂, ŷ ) = (x, y ) + (ξ, η) + higher-order terms to be ignored
• substitute into defining condition:
d(y + η)
= f (x + ξ, y + η)
d(x + ξ)
• after the dust settles:
∂η
∂η
∂ξ ∂f
∂f
∂ξ
+f
−
=
ξ+
η
−f2
∂x
∂y
∂x
∂y
∂x
∂y
• first-order linear PDE for ξ(x, y ) and η(x, y )
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
• Example:
dy
= y so f (x, y ) = y
dx
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
dy
= y so f (x, y ) = y
dx
• try ξ = ax + by + c and η = αx + βy + γ
• Example:
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
dy
= y so f (x, y ) = y
dx
• try ξ = ax + by + c and η = αx + βy + γ
• substitute:
• Example:
α + (β − a)y − by 2 = αx + βy + γ
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
dy
= y so f (x, y ) = y
dx
• try ξ = ax + by + c and η = αx + βy + γ
• substitute:
• Example:
α + (β − a)y − by 2 = αx + βy + γ
•
match coefficients:
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
dy
= y so f (x, y ) = y
dx
• try ξ = ax + by + c and η = αx + βy + γ
• substitute:
• Example:
α + (β − a)y − by 2 = αx + βy + γ
•
match coefficients:
1:
α=γ
x:
0=α
y:
β−a=β
2
y :
b=0
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
dy
= y so f (x, y ) = y
dx
• try ξ = ax + by + c and η = αx + βy + γ
• substitute:
• Example:
α + (β − a)y − by 2 = αx + βy + γ
•
match coefficients:
1:
α=γ
x:
0=α
y:
2
y :
β−a=β
b=0
ξ=c
=⇒
η = βy
∂η
∂η
∂ξ ∂ξ
∂f
∂f
+f
−
−f2
=
ξ+
η
∂x
∂y
∂x
∂y
∂x
∂y
dy
= y so f (x, y ) = y
dx
• try ξ = ax + by + c and η = αx + βy + γ
• substitute:
• Example:
α + (β − a)y − by 2 = αx + βy + γ
•
match coefficients:
1:
α=γ
x:
0=α
y:
2
y :
•
β−a=β
ξ=c
=⇒
η = βy
b=0
~ = (1, 0) and X
~ = (0, y ) are symmetry vector fields
so X
Topics for another time
• Classifying first-order ODEs by symmetry
Topics for another time
• Classifying first-order ODEs by symmetry
• Symmetries of higher-order ODEs
Topics for another time
• Classifying first-order ODEs by symmetry
• Symmetries of higher-order ODEs
• Symmetries of PDEs
Topics for another time
• Classifying first-order ODEs by symmetry
• Symmetries of higher-order ODEs
• Symmetries of PDEs
• Finding invariant solutions (example: fundamental solution for
the heat equation)
Topics for another time
• Classifying first-order ODEs by symmetry
• Symmetries of higher-order ODEs
• Symmetries of PDEs
• Finding invariant solutions (example: fundamental solution for
the heat equation)
• Algebraic structure of symmetries: Lie groups and Lie algebras
Topics for another time
• Classifying first-order ODEs by symmetry
• Symmetries of higher-order ODEs
• Symmetries of PDEs
• Finding invariant solutions (example: fundamental solution for
the heat equation)
• Algebraic structure of symmetries: Lie groups and Lie algebras
• Variational symmetries
Topics for another time
• Classifying first-order ODEs by symmetry
• Symmetries of higher-order ODEs
• Symmetries of PDEs
• Finding invariant solutions (example: fundamental solution for
the heat equation)
• Algebraic structure of symmetries: Lie groups and Lie algebras
• Variational symmetries
• Nonclassical symmetries
A few references
A few references
Peter Hydon, Symmetry Methods for Differential
Equations: A Beginner’s Guide, Cambridge, 2000.
A few references
Peter Hydon, Symmetry Methods for Differential
Equations: A Beginner’s Guide, Cambridge, 2000.
Peter Olver, Applications of Lie Groups to Differential Equations 2nd ed., Springer, 1993.