Lengths of simple loops on surfaces with hyperbolic metrics Geometry & Topology G
... and the set of homotopy classes of simple loops and arcs. The length pairing sends a hyperbolic metric and a homotopy class of a simple loop or arc to the length of the geodesic in its homotopy class. In this paper, we study this pairing function using the Fenchel–Nielsen coordinates on Teichmüller ...
... and the set of homotopy classes of simple loops and arcs. The length pairing sends a hyperbolic metric and a homotopy class of a simple loop or arc to the length of the geodesic in its homotopy class. In this paper, we study this pairing function using the Fenchel–Nielsen coordinates on Teichmüller ...
Spherical Trigonometry—Laws of Cosines and Sines Students use
... the center of the sphere to points A, B, and C are radii of a unit sphere, so their lengths are all one. This means that cos(a) = B · C. So let’s figure out the vectors B and C from the origin to the points B and C respectively. First, let’s rotate the sphere along the axis through A until B lies i ...
... the center of the sphere to points A, B, and C are radii of a unit sphere, so their lengths are all one. This means that cos(a) = B · C. So let’s figure out the vectors B and C from the origin to the points B and C respectively. First, let’s rotate the sphere along the axis through A until B lies i ...
2. 1.2. Exercises
... 1. 13.1. The problem of the bridge .............................................................................. 117 2. 13.2. The problem of the camel ............................................................................... 117 3. 13.3. The Fermat point of a triangle ........................ ...
... 1. 13.1. The problem of the bridge .............................................................................. 117 2. 13.2. The problem of the camel ............................................................................... 117 3. 13.3. The Fermat point of a triangle ........................ ...
Which quadrilateral MUST be a parallelogram? A. B. C. D. MKN ∆ ∆
... 30 units long and KN is 10 units long. If MN is 12 units long, what is JL ? ...
... 30 units long and KN is 10 units long. If MN is 12 units long, what is JL ? ...
MA.912.G.3.3
... On the coordinate plane at right quadrilateral PQRS has vertices with integer coordinates. ...
... On the coordinate plane at right quadrilateral PQRS has vertices with integer coordinates. ...
Using Midpoint Formulas 1.3
... c. What is the coordinate of the midpoint M? d. Compare the coordinates of A, B, and M. How is the coordinate of the midpoint M related to the coordinates of A and B? e. Use the result of part (d) to write a rule for finding the midpoint of any two points on a number line. Choose two points on a num ...
... c. What is the coordinate of the midpoint M? d. Compare the coordinates of A, B, and M. How is the coordinate of the midpoint M related to the coordinates of A and B? e. Use the result of part (d) to write a rule for finding the midpoint of any two points on a number line. Choose two points on a num ...
12.1 Exercises
... most 2. But we are also given that z 艋 0, so the points lie on or below the xy-plane. Thus the given inequalities represent the region that lies between (or on) the spheres x 2 ⫹ y 2 ⫹ z 2 苷 1 and x 2 ⫹ y 2 ⫹ z 2 苷 4 and beneath (or on) the xy-plane. It is sketched in Figure 13. ...
... most 2. But we are also given that z 艋 0, so the points lie on or below the xy-plane. Thus the given inequalities represent the region that lies between (or on) the spheres x 2 ⫹ y 2 ⫹ z 2 苷 1 and x 2 ⫹ y 2 ⫹ z 2 苷 4 and beneath (or on) the xy-plane. It is sketched in Figure 13. ...
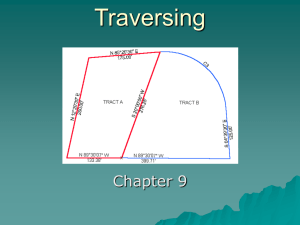
Traversing - FacStaff Home Page for CBU
... Rigorous but best method based on probabilistic approach which models the occurrence of random errors. Angle and distance measurements are adjusted simultaneously. Most computer programs employ a least square adjustment methodology. For more information on Least Squares Method see Chapter 15 in your ...
... Rigorous but best method based on probabilistic approach which models the occurrence of random errors. Angle and distance measurements are adjusted simultaneously. Most computer programs employ a least square adjustment methodology. For more information on Least Squares Method see Chapter 15 in your ...
Plane Separation, Interior of Angles, Crossbar Theorem
... …neither is C between A and B, nor is A between B and C. We will assume that C is between A and B. This means that AC + CB = AB by the definition of betweeness. We may add BC to both sides of the equation to get AC + CB + BC = AB + BC. On the right this is actually AC from the equation in the first ...
... …neither is C between A and B, nor is A between B and C. We will assume that C is between A and B. This means that AC + CB = AB by the definition of betweeness. We may add BC to both sides of the equation to get AC + CB + BC = AB + BC. On the right this is actually AC from the equation in the first ...
Geometry Notes Ch 13
... linkage between geometry and algebra. One key to understanding this ‘linkage’ is to understand the different ‘dialects’ we speak in the mathematical language. Relate this to the many ‘dialects’ within the United States. The vast majority of citizens of the United States speak an English ‘dialect’. I ...
... linkage between geometry and algebra. One key to understanding this ‘linkage’ is to understand the different ‘dialects’ we speak in the mathematical language. Relate this to the many ‘dialects’ within the United States. The vast majority of citizens of the United States speak an English ‘dialect’. I ...
Use the Geometry Calculator
... Determines the 3D unit normal vector to a plane defined by the three points p1, p2, and p3. The orientation of the normal vector is such that the given points go counterclockwise with respect to the normal. The following illustrations show how normal vectors are calculated: The nor function calculat ...
... Determines the 3D unit normal vector to a plane defined by the three points p1, p2, and p3. The orientation of the normal vector is such that the given points go counterclockwise with respect to the normal. The following illustrations show how normal vectors are calculated: The nor function calculat ...
Geometry Honors Chapter 1: Foundations for Geometry
... A pair of opposite rays that both contain point R ...
... A pair of opposite rays that both contain point R ...
Trigonometric
... perpendicular to the opposite side (or an extension of the opposite side. We are going to draw an altitude in our triangle from the point where the terminal side of our angle intersect the unit circle to the xaxis. In an equilateral triangle, altitudes have the property that they bisect (cut into tw ...
... perpendicular to the opposite side (or an extension of the opposite side. We are going to draw an altitude in our triangle from the point where the terminal side of our angle intersect the unit circle to the xaxis. In an equilateral triangle, altitudes have the property that they bisect (cut into tw ...
Vectors - Kaysons Education
... Vectors whose initial point is not specified are called free vectors. As shown in ...
... Vectors whose initial point is not specified are called free vectors. As shown in ...
classwork geometry 5/13/2012
... . Vectors may also be labeled as a single letter with an arrow, , or a single bold face letter, such as vector v. The length (magnitude) of a vector v is written |v|. Length is always a non-negative real number. C Addition (subtraction?) of vectors. One can formally define an operation of addition o ...
... . Vectors may also be labeled as a single letter with an arrow, , or a single bold face letter, such as vector v. The length (magnitude) of a vector v is written |v|. Length is always a non-negative real number. C Addition (subtraction?) of vectors. One can formally define an operation of addition o ...
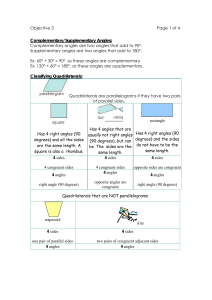
Objective 3 Page 1 of 4 Complementary/Supplementary Angles
... Complementary angles are two angles that add to 90°. Supplementary angles are two angles that add to 180°. Ex. 60° + 30° = 90°, so these angles are complementary. Ex. 120° + 60° = 180°, so these angles are supplementary. ...
... Complementary angles are two angles that add to 90°. Supplementary angles are two angles that add to 180°. Ex. 60° + 30° = 90°, so these angles are complementary. Ex. 120° + 60° = 180°, so these angles are supplementary. ...
Curvilinear coordinates
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible (a one-to-one map) at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.Well-known examples of curvilinear coordinate systems in three-dimensional Euclidean space (R3) are Cartesian, cylindrical and spherical polar coordinates. A Cartesian coordinate surface in this space is a plane; for example z = 0 defines the x-y plane. In the same space, the coordinate surface r = 1 in spherical polar coordinates is the surface of a unit sphere, which is curved. The formalism of curvilinear coordinates provides a unified and general description of the standard coordinate systems.Curvilinear coordinates are often used to define the location or distribution of physical quantities which may be, for example, scalars, vectors, or tensors. Mathematical expressions involving these quantities in vector calculus and tensor analysis (such as the gradient, divergence, curl, and Laplacian) can be transformed from one coordinate system to another, according to transformation rules for scalars, vectors, and tensors. Such expressions then become valid for any curvilinear coordinate system.Depending on the application, a curvilinear coordinate system may be simpler to use than the Cartesian coordinate system. For instance, a physical problem with spherical symmetry defined in R3 (for example, motion of particles under the influence of central forces) is usually easier to solve in spherical polar coordinates than in Cartesian coordinates. Equations with boundary conditions that follow coordinate surfaces for a particular curvilinear coordinate system may be easier to solve in that system. One would for instance describe the motion of a particle in a rectangular box in Cartesian coordinates, whereas one would prefer spherical coordinates for a particle in a sphere. Spherical coordinates are one of the most used curvilinear coordinate systems in such fields as Earth sciences, cartography, and physics (in particular quantum mechanics, relativity), and engineering.