Download Trigonometric

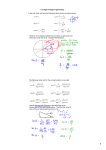
Trigonometric Functions:
The Unit Circle
Section 4.2
Objectives
• Find a point on the unit circle given one
coordinate and the quadrant in which the point
lies.
• Determine the coordinates of a point on the
unit circle given a point on the unit circle.
• State the sign of the sine or cosine value of
an angle based on the quadrant in which the
terminal side of an angle occurs.
• State the sine and cosine values of an angle
(measured in radians) where the angles have a
measure of 0,
   
, , , , and 
6 4 3 2
Objectives
• Determine the tangent, cotangent, secant,
and cosecant values of an angle given a point
on the unit circle.
• State the sign of the tangent, cotangent,
secant, and cosecant value of an angle based
on the quadrant in which the terminal side of
an angle occurs.
• Determine the tangent, cotangent, secant,
and cosecant values of an angle (measured in
radians) where the angles have a measure of
   
0, , , , , and 
6 4 3 2
Vocabulary
•
•
•
•
•
•
•
•
•
quadrant
sine of an angle
cosine of an angle
terminal side of an angle
initial side of an angle
tangent of an angle
cotangent of an angle
secant of an angle
cosecant of an angle
Unit Circle
Each point on the unit
circles has an x-coordinate
and a y-coordinate. Any
angle, θ, in standard
position (vertex at the
origin and initial side on the
positive x-axis) will have a
terminal side that
intersects the unit circle in
a single point. We define
the sin(θ) as the value of
the y-coordinate of the
point of intersection
between the terminal side
of the angle and the unit
circle. We define the cos(θ)
as the value of the xcoordinate of the point of
intersection between the
terminal side of the angle
and the unit circle.
(cos(θ), sin(θ))=(x, y)
θ
4 
P , y 
5

If the point
is on the unit
circle in quadrant IV, then find y.
The coordinates of all points
on the unit circle satisfy the
equation
x2 y2 1
This means that all we have
to do is plug in the value of
the x-coordinate into the
equation and solve for y.
continued on next slide
4 
P , y 
5

If the point
is on the unit
circle in quadrant IV, then find y.
2
4
2

y
1
 
5
16
y2 1
25
16
2
y 1
25
25 16
2
y 

25 25
9
2
y 
25
continued on next slide
4 
P , y 
5

If the point
is on the unit
circle in quadrant IV, then find y.
9
y 
25
3
y 
5
Since there can only be one answer to
this question, we have to determine if
the answer is the positive number or
the negative number. We are told that
the point is in quadrant IV. In quadrant
IV, the x-values are positive and the yvalues are negative. This means that
the correct answer for our problem is
3
y 
5
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.
The first thing that we want to do
for this problem put the point P(t)
on the picture.
P(t)=(0.141, 0.99)
1. P t   
In order to answer part 1, it will
help to draw the angle t + π on
the picture. Keep in mind that
the distance π is half way around
the circle.
t+π
t
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.
Because of the symmetries of the
circle, the new point is the same
horizontal distance away from the
from the y-axis as the original point.
It is just in the opposite direction.
Similarly, the new point is the same
vertical distance from the x-axis as
the original point. It is just in the
opposite direction. This means that
the only thing that changes to the
coordinates as we go from the old
point to the new point is the sign of
each coordinate. Thus
P(t)=(0.141, 0.99)
t+π
t
1. P t     (0.141,  0.99)
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.
In order to answer part 2, it will
help to draw the angle -t on the
picture. Keep in mind that the
angle –t is the same distance as
the angle t only in the clockwise
direction.
2. P t 
Because of the symmetries of the
circle, the new point is the same
horizontal distance away from the
from the y-axis as the original point.
This time it is in the same direction.
P(t)=(0.141, 0.99)
t
-t
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.
Similarly, the new point is the
same vertical distance from the
x-axis as the original point. It is
just in the opposite direction.
This means that the only thing
that changes to the coordinates
as we go from the old point to the
new point is the sign of the ycoordinate. Thus
2. P t   (0.141,  0.99)
P(t)=(0.141, 0.99)
t
-t
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.In order to answer part 3, it will
help to draw the angle t - π on
the picture. Keep in mind that
the distance π is half way around
the circle. In this case since it is
– π we will be going clockwise half
way around the circle
3. P t   
Notice that since the beginning of
the angle is t (which is positive), we
start off in the counter-clockwise
direction. Once we get to t, we
turn and go back in the clockwise
direction a distance of π.
P(t)=(0.141, 0.99)
t
t-π
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of
each
point
indicated
below.Because of the symmetries of the
circle, the new point is the same
horizontal distance away from the
from the y-axis as the original point.
It is just in the opposite direction.
Similarly, the new point is the same
vertical distance from the x-axis as
the original point. It is just in the
opposite direction. This means that
the only thing that changes to the
coordinates as we go from the old
point to the new point is the sign of
each coordinate. Thus
P(t)=(0.141, 0.99)
t
t-π
3. P t     (0.141,  0.99)
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.
In order to answer part 4, it will
help to draw the angle -t - π on
the picture. Keep in mind that
the distance π is half way around
the circle. This time we start in
the clockwise direction a distance
of t and then continue in the
clockwise direction half way
around the circle further.
4. P t   
P(t)=(0.141, 0.99)
t
-t - π
continued on next slide
If P(t) has coordinates
(0.141, 0.99), find the coordinates
of each point indicated below.
Because of the symmetries of the
circle, the new point is the same
horizontal distance away from the
from the y-axis as the original point.
It is just in the opposite direction.
Similarly, the new point is the same
vertical distance from the x-axis as
the original point. This however is in
the same direction. This means that
the only thing that changes to the
coordinates as we go from the old
point to the new point is the sign of
the x-coordinate. Thus
4. P  t     (.0141, 0.99)
P(t)=(0.141, 0.99)
t
-t - π
Find the terminal point P(x, y) on
the unit circle determined by the
value of t 

point of intersection
2
Since our angle is the one
that has a terminal side that
runs along the positive y-axis,
this terminal side of the
angle intersects the unit
circle at (0, 1). This means
that the x-coordinate of the
point is 0 and the ycoordinate of the point is -1.

2
Sine and Cosines for Basic
Quadrant I Angles
For the next few slides we are going to find the
coordinates of the points where the terminal side
of three standard angles intersect with the unit
circle. This will allow us to define the sine and
cosine values for the following quadrant I angles:
 

, , and
6 4
3
If t 

4
, find the sin(t) and cos(t).
For this problem, we are
going to draw a right
triangle the length of
whose legs are equal to
the coordinates of the
point where the angle
intersects the unit
circle.
The dark blue triangle
that we have drawn has
two non-right angles in
it. One of the angles is
π/4 (or 45 degrees).
Since the sum of the
angles of a triangle add
up to 180 degrees, the
other non-right angle
must have a measure of
45 degrees also.
continued on next slide
If t 

4
, find the sin(t) and cos(t).
This makes the dark
blue triangle an
isosceles triangle. In an
isosceles triangle the
lengths of the sides
opposite the angles that
are equal are also equal.
This means that the
sides marked x and y
are equal in length.
y
x
Now a right satisfies
the Pythagorean
Theorem. This means
x y 1
2
2
The hypotenuse of the
triangle is equal to 1 since it is
the radius of a unit circle.
continued on next slide
If t 

4
, find the sin(t) and cos(t).
Since both x and y are the same
length, we can replace y with x
(we could replace x with y) and
end up at the same place. Once
we do this we can solve the
equation for x.
2
2
x y 1
x x 1
2
y
2
2x 2  1
x
1
x 
2
2
1
x 
2
continued on next slide
If t 

4
, find the sin(t) and cos(t).
Since x is a length, x must be
positive. Thus
2
x 
2
Notice that x has the
denominator rationalized.
Since x and y are the same,
then
x
2
y 
2
Thus

2
sin  
4 2
y
and

2
cos  
4 2
If t 

3
, find the sin(t) and cos(t).
Our aim here is to get a right
triangle whose legs have the
same measure as the
coordinates of the point
where the terminal side of
the angle π/3 (60 degrees)
intersects the unit circle.
This process will take a little
more work than with the 45
degree angle. We will start
by completing a triangle by
drawing the red line
connecting the points where
the initial side and terminal
side of the angle intersect
the unit circle.
continued on next slide
If t 

3
, find the sin(t) and cos(t).
Now we will put some labels
on our figure. Side U and
side V are both of length 1
since they are both radii of a
unit circle. This means that
our triangle is an isosceles
triangle. In an isosceles
triangle the angles opposite
the equal sides are equal.
Thus the marked angles are
equal. We will say they
measure a. We now need to
find the measure of each of
those angles. The three
angle of the triangle add up
to 180. We know one of the
angles is 60. Thus we can
calculate a.
U
W
a
a
V
continued on next slide
If t   , find the sin(t) and cos(t).
3
To find a we have
60  a  a  180
60  2a  180
2a  120
a  60
Since all of the angles of our
triangle are the same
measure, we have an
equiangular (also equilateral)
triangle.
U
W
a
a
V
continued on next slide
If t   , find the sin(t) and cos(t).
3
An altitude of a triangle is a line
that goes from one vertex and is
perpendicular to the opposite side
(or an extension of the opposite
side.
We are going to draw an altitude in
our triangle from the point where
the terminal side of our angle
intersect the unit circle to the xaxis. In an equilateral triangle,
altitudes have the property that
they bisect (cut into two equal
pieces) both the angle from which
they original and the opposite side.
This means that the distance from
the origin to the intersection of
the altitude and the x-axis is ½
because the length of the original
side was 1.
U
W
a
a
V
continued on next slide
If t   , find the sin(t) and cos(t).
3
We can now draw a right
triangle. The length of the leg
along the positive x-axis is ½.
This means that the xcoordinate of our point is ½.
The length of the hypotenuse
of the triangle is 1 since it is a
radius of a unit circle. Using
this and the Pythagorean
Theorem, we can calculate y.
2
1
2

y
1
 
2
U
a
W
y
a
½
V
continued on next slide
If t   , find the sin(t) and cos(t).
3
1
y2 1
4
1
2
y 1
4
3
2
y 
4
3
y 
4
U
Thus
½
3
2

3
sin  
3 2
W
y
a
Since y represents a length,
it must be positive. Thus
y 
a
and

1
cos   
3 2
V
If t 

6
, find the sin(t) and cos(t).
The same process that was
used for π/3 will work for
π/6. The only difference
is that we will make the
first triangle by connecting
the point where the
terminal side of the angle
intersections the unit
circle and where the y-axis
intersects the unit circle.
We know that the angle in
this triangle whose vertex
is the origin is 60 degrees
since it is complementary
to the π/6 (30 degree)
angle that we are given.
continued on next slide
If t 

6
, find the sin(t) and cos(t).
The process then continues
with the altitude
intersecting the y-axis
(instead of the x-axis as in
the previous example).
Thus

1
sin  
6 2
and

3
cos  
6 2
Other Trigonometric Functions
Once we have defined the sine and the cosine for an
angle, we can define all of the other trigonometric
functions in terms of the sine and cosine functions.
Quotient Identities
sin(t )
tan(t ) 
cos(t )
cos(t )
cot(t ) 
sin(t )
Reciprocal Identites
1
sin(t ) 
csc(t )
cos(t ) 
1
sec(t )
1
tan(t ) 
cot(t )
1
csc(t ) 
sin(t )
sec(t ) 
1
cos(t )
1
cot(t ) 
tan(t )
Pythagorean Identity
sin (t )  cos (t )  1
2
2
tan (t )  1  sec (t )
2
2
1  cot (t )  csc (t )
2
2