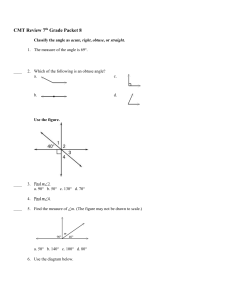
SYMMETRIES OF MONOCORONAL TILINGS 1. Introduction The
... out of 16 wallpaper groups: any except ∗×. If such tiling is 1-periodic then its symmetry group is one of four frieze groups: ∞∞, ∞×, ∞∗, or 22∞. In particular, every such tiling is crystallographic or 1-periodic. Remark 2.3. It turns out that the 1-periodic tilings in Theorem 2.2 consist of 1-perio ...
... out of 16 wallpaper groups: any except ∗×. If such tiling is 1-periodic then its symmetry group is one of four frieze groups: ∞∞, ∞×, ∞∗, or 22∞. In particular, every such tiling is crystallographic or 1-periodic. Remark 2.3. It turns out that the 1-periodic tilings in Theorem 2.2 consist of 1-perio ...
Conjectures
... bases and is equal in length to the average of the lengths of the bases. (Lesson 5.4) ...
... bases and is equal in length to the average of the lengths of the bases. (Lesson 5.4) ...
Conjecture - Miami Killian Senior High School
... 93 Minimal Path Conjecture - If points A and B are on one side of line l, then the minimal path from point A to line l to point B is found by reflecting point B over line l, drawing segment AB , then drawing segments AC and CB where point C is the point of intersection of segment AB and line l. ...
... 93 Minimal Path Conjecture - If points A and B are on one side of line l, then the minimal path from point A to line l to point B is found by reflecting point B over line l, drawing segment AB , then drawing segments AC and CB where point C is the point of intersection of segment AB and line l. ...
CONJECTURES - Discovering Geometry Chapter 2 C
... Minimal Path Conjecture - If points A and B are on one side of line l , then the minimal path from point A to line l to point B is found by reflecting point B over line l , drawing segment AB ¢ , then drawing segments AC and CB where point C is the point of intersection of segment AB ¢ and line l . ...
... Minimal Path Conjecture - If points A and B are on one side of line l , then the minimal path from point A to line l to point B is found by reflecting point B over line l , drawing segment AB ¢ , then drawing segments AC and CB where point C is the point of intersection of segment AB ¢ and line l . ...
Conjectures for Geometry for Math 70 By I. L. Tse Chapter 2
... 3. Corresponding Angles Conjecture, or CA Conjecture: If two parallel lines are cut by a transversal, then corresponding angles are congruent. 4. Alternate Interior Angles Conjecture, or AIA Conjecture: If two parallel lines are cut by a transversal, then alternate interior angles are congruent. 5. ...
... 3. Corresponding Angles Conjecture, or CA Conjecture: If two parallel lines are cut by a transversal, then corresponding angles are congruent. 4. Alternate Interior Angles Conjecture, or AIA Conjecture: If two parallel lines are cut by a transversal, then alternate interior angles are congruent. 5. ...
Geometer`s Sketchpad—Techno Polly
... After the rotation, the new radius and its point of intersection are highlighted. The center point is still “marked” as the point of rotation. To rotate the radius, simply use the Transform and Rotate options again. The 120 degrees should still be in the pop-up window; so to complete the rotation, c ...
... After the rotation, the new radius and its point of intersection are highlighted. The center point is still “marked” as the point of rotation. To rotate the radius, simply use the Transform and Rotate options again. The 120 degrees should still be in the pop-up window; so to complete the rotation, c ...
Slides for Nov. 12, 2014, lecture
... manifold; the collection of all possible physical colors is as well, since an individual physical color can be uniquely identified by the values (modes of specification) of its hue, saturation and brightness, all of which vary continuously ...
... manifold; the collection of all possible physical colors is as well, since an individual physical color can be uniquely identified by the values (modes of specification) of its hue, saturation and brightness, all of which vary continuously ...
geometry - Swampscott High School
... A diagram of part of a baseball field and some of its dimensions are shown below. Point F represents First Base, point S represents Second Base, point T represents Third Base, point H represents Home Plate, and point P represents another location on the baseball field. ...
... A diagram of part of a baseball field and some of its dimensions are shown below. Point F represents First Base, point S represents Second Base, point T represents Third Base, point H represents Home Plate, and point P represents another location on the baseball field. ...
Atomic orbitals, symmetry, and coordination polyhedra
... therefore remains unaltered by any symmetry operations. For this reason all of the symmetry properties of a spherical harmonic C, and thus of the corresponding wave function or atomic orbital, are contained in its angular component U(u)·F(f). Furthermore, each of the three factors of C (Eq. (3)) gen ...
... therefore remains unaltered by any symmetry operations. For this reason all of the symmetry properties of a spherical harmonic C, and thus of the corresponding wave function or atomic orbital, are contained in its angular component U(u)·F(f). Furthermore, each of the three factors of C (Eq. (3)) gen ...
[edit] Star polyhedra
... every face is the same regular polygon; it also implies that every vertex is regular). Quasi-regular if it is vertex-transitive and edge-transitive (and hence has regular faces) but not face-transitive. A quasi-regular dual is face-transitive and edge-transitive (and hence every vertex is regular) b ...
... every face is the same regular polygon; it also implies that every vertex is regular). Quasi-regular if it is vertex-transitive and edge-transitive (and hence has regular faces) but not face-transitive. A quasi-regular dual is face-transitive and edge-transitive (and hence every vertex is regular) b ...
4. Shape, Dimension, and Geometric Relationships
... i. Prove the Pythagorean identity sin2(θ) + cos2(θ) = 1. (CCSS: F-TF.8) ii. Use the Pythagorean identity to find sin(θ), cos(θ), or tan(θ) given sin(θ), cos(θ), or tan(θ) and the quadrant of the angle. (CCSS: F-TF.8) e. Understand and apply theorems about circles. (CCSS: G-C) i. Identify and describ ...
... i. Prove the Pythagorean identity sin2(θ) + cos2(θ) = 1. (CCSS: F-TF.8) ii. Use the Pythagorean identity to find sin(θ), cos(θ), or tan(θ) given sin(θ), cos(θ), or tan(θ) and the quadrant of the angle. (CCSS: F-TF.8) e. Understand and apply theorems about circles. (CCSS: G-C) i. Identify and describ ...
Geometry 1
... a line segment, the distance formula, and various forms of equations of lines and circles. ...
... a line segment, the distance formula, and various forms of equations of lines and circles. ...
360
... The perpendicular from the center of a circle to a chord is the bisector of the chord. Chord Distance to Center Conjecture Two congruent chords in a circle are equidistant from the center of the circle. Perpendicular Bisector of a Chord Conjecture The perpendicular bisector of a chord passes through ...
... The perpendicular from the center of a circle to a chord is the bisector of the chord. Chord Distance to Center Conjecture Two congruent chords in a circle are equidistant from the center of the circle. Perpendicular Bisector of a Chord Conjecture The perpendicular bisector of a chord passes through ...
Pairs of Pants and Congruence Laws of Geometry - Rose
... hyperbolic geometry for higher genus surfaces hyperbolic surface with geometry is hard to picture - we will use the pants model instead unfolded hyperbolic surface geometry - circles orthogonal to the boundary are the lines ...
... hyperbolic geometry for higher genus surfaces hyperbolic surface with geometry is hard to picture - we will use the pants model instead unfolded hyperbolic surface geometry - circles orthogonal to the boundary are the lines ...
Mirror symmetry (string theory)
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.Mirror symmetry was originally discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously.Today mirror symmetry is a major research topic in pure mathematics, and mathematicians are working to develop a mathematical understanding of the relationship based on physicists' intuition. Mirror symmetry is also a fundamental tool for doing calculations in string theory, and it has been used to understand aspects of quantum field theory, the formalism that physicists use to describe elementary particles. Major approaches to mirror symmetry include the homological mirror symmetry program of Maxim Kontsevich and the SYZ conjecture of Andrew Strominger, Shing-Tung Yau, and Eric Zaslow.













![[edit] Star polyhedra](http://s1.studyres.com/store/data/000129689_1-21c3cefe8dffc208c8fed163027e6a92-300x300.png)