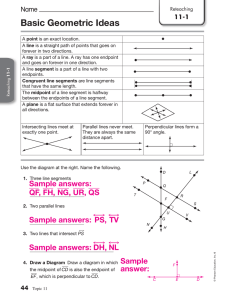
HS Standards Course Transition Document 2012
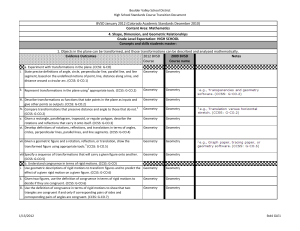
... 1. Objects in the plane can be transformed, and those transformations can be described and analyzed mathematically. Evidence Outcomes 2012 BVSD 2009 BVSD Notes Course Course name name a. Experiment with transformations in the plane. (CCSS: G-CO) i. State precise definitions of angle, circle, perpend ...
... 1. Objects in the plane can be transformed, and those transformations can be described and analyzed mathematically. Evidence Outcomes 2012 BVSD 2009 BVSD Notes Course Course name name a. Experiment with transformations in the plane. (CCSS: G-CO) i. State precise definitions of angle, circle, perpend ...
Lesson 8-3: Proving Triangles Similar
... to width ratio. This ratio (the golden ratio) is found to be pleasing to the eye for most people. The same holds true for similar triangles (or other polygons for that matter). One way to think about similar triangles is two triangles that are not identical but do balance each other nicely. Thus, yo ...
... to width ratio. This ratio (the golden ratio) is found to be pleasing to the eye for most people. The same holds true for similar triangles (or other polygons for that matter). One way to think about similar triangles is two triangles that are not identical but do balance each other nicely. Thus, yo ...
SS1 Classifying shapes
... Learners who struggle may be asked to find shapes corresponding to one criterion at a time (e.g. “Regular or irregular?”). When they have done this, they might then be encouraged to use two-way classifications such as those found on the grids. Learners who find the task straightforward should be pre ...
... Learners who struggle may be asked to find shapes corresponding to one criterion at a time (e.g. “Regular or irregular?”). When they have done this, they might then be encouraged to use two-way classifications such as those found on the grids. Learners who find the task straightforward should be pre ...
GEOMETRY FINAL EXAM MATERIAL
... Ratios and Proportions o Be able to set up and solve proportions Geometric Mean o Be able to find the geometric mean of two numbers o Geometric Mean Triangle Altitude Conjecture, Geometric Mean Triangle Leg Conjecture Special Right Triangles o 30-60-90 , 45-45-90 Right Triangle Trigonometry ...
... Ratios and Proportions o Be able to set up and solve proportions Geometric Mean o Be able to find the geometric mean of two numbers o Geometric Mean Triangle Altitude Conjecture, Geometric Mean Triangle Leg Conjecture Special Right Triangles o 30-60-90 , 45-45-90 Right Triangle Trigonometry ...
The Mathematical Universe
... simple mathematical structures can provide good approximations of certain aspects of more complex mathematical structures. In other words, our successful theories are not mathematics approximating physics, but mathematics approximating mathematics. The MUH makes the testable prediction that further ...
... simple mathematical structures can provide good approximations of certain aspects of more complex mathematical structures. In other words, our successful theories are not mathematics approximating physics, but mathematics approximating mathematics. The MUH makes the testable prediction that further ...
FIELD_INTRIL
... All pseudo-moduli get non-tachyonic masses at one-loop. SUSY broken: Vacua (meta) stable (we'll discuss tunneling soon). Vacua mysterious in electric description. Not semi-classical, very quantum mechanical. ...
... All pseudo-moduli get non-tachyonic masses at one-loop. SUSY broken: Vacua (meta) stable (we'll discuss tunneling soon). Vacua mysterious in electric description. Not semi-classical, very quantum mechanical. ...
Symmetry and Tessellations
... looking for. Think about the definitions and questions; see how exotic the examples can be. At all cost you should avoid “hit-and-run mathematics”: coming up with a quick answer without thinking about it too deeply. This (bad) practice would keep all the really interesting ideas and patterns hidden ...
... looking for. Think about the definitions and questions; see how exotic the examples can be. At all cost you should avoid “hit-and-run mathematics”: coming up with a quick answer without thinking about it too deeply. This (bad) practice would keep all the really interesting ideas and patterns hidden ...
Progression of GEOMETRY PROPERTIES OF SHAPE
... Draw 2-D shapes using given dimensions and angles Recognise, describe and build simple 3-D shapes, including making nets Compare and classify geometric shapes based on their properties and sizes and find unknown angles in any triangles, quadrilaterals, and regular polygons Illustrate and name parts ...
... Draw 2-D shapes using given dimensions and angles Recognise, describe and build simple 3-D shapes, including making nets Compare and classify geometric shapes based on their properties and sizes and find unknown angles in any triangles, quadrilaterals, and regular polygons Illustrate and name parts ...
Polyhedra and PL Manifolds (Lecture 17)
... If K ⊆ Rn and L ⊆ Rm are polyhedra, we say that a map f : K → L is piecewise linear if the underlying map f : K → Rm is piecewise linear. Remark 5. Let f : K → L be a piecewise linear homeomorphism between polyhedra. Then the inverse map f −1 : L → K is again piecewise linear. To see this, choose an ...
... If K ⊆ Rn and L ⊆ Rm are polyhedra, we say that a map f : K → L is piecewise linear if the underlying map f : K → Rm is piecewise linear. Remark 5. Let f : K → L be a piecewise linear homeomorphism between polyhedra. Then the inverse map f −1 : L → K is again piecewise linear. To see this, choose an ...
Unit 31 Angles and Symmetry
... Shapes have line symmetry if a mirror could be placed so that one side is an exact reflection of the other. These imaginary 'mirror lines' are shown by dotted lines in the diagrams below. ...
... Shapes have line symmetry if a mirror could be placed so that one side is an exact reflection of the other. These imaginary 'mirror lines' are shown by dotted lines in the diagrams below. ...
x - Wampatuck - Grade 6
... The general pattern is circle-square-circle-triangle, but the square and triangle are increased by 1 in each step of the pattern. 4. In a contest, the first place team gets _12 of the million-dollar prize. The second place team gets _12 of the remaining money. Each team after that gets _12 of the re ...
... The general pattern is circle-square-circle-triangle, but the square and triangle are increased by 1 in each step of the pattern. 4. In a contest, the first place team gets _12 of the million-dollar prize. The second place team gets _12 of the remaining money. Each team after that gets _12 of the re ...
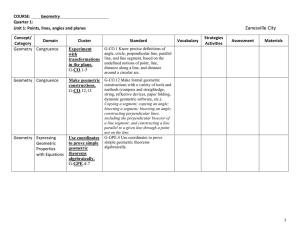
Zanesville City Schools
... Use coordinates to prove simple geometric theorems algebraically. G-GPE.4-7 Prove geometric G-CO.8 Explain how the criteria for triangle congruence (ASA, SAS, and theorems. SSS) follow from the definition of G-CO.9-11 ...
... Use coordinates to prove simple geometric theorems algebraically. G-GPE.4-7 Prove geometric G-CO.8 Explain how the criteria for triangle congruence (ASA, SAS, and theorems. SSS) follow from the definition of G-CO.9-11 ...
Answer - Imagine School at Lakewood Ranch
... Check To draw an accurate circle graph, make sure the sum of the angle measures equals 360°. Label each section of the graph with the category and percent. Give the graph a title. Answer: ...
... Check To draw an accurate circle graph, make sure the sum of the angle measures equals 360°. Label each section of the graph with the category and percent. Give the graph a title. Answer: ...
Part VI - TTU Physics
... • Consequences of BZ symmetries for bandstructures: Wavefunctions ψk(r) can be expressed such that they have definite transformation properties under crystal symmetry operations. ...
... • Consequences of BZ symmetries for bandstructures: Wavefunctions ψk(r) can be expressed such that they have definite transformation properties under crystal symmetry operations. ...
Was there a Revolution in Geometry in the Nineteenth Century?
... the long running dispute over the status of the parallel postulate. The major change occurred when Lobachevskii and Bolyai became the first to publish work developing what they claimed to be a consistent non-Euclidean geometry. But the revolution was not complete until the mathematical world took no ...
... the long running dispute over the status of the parallel postulate. The major change occurred when Lobachevskii and Bolyai became the first to publish work developing what they claimed to be a consistent non-Euclidean geometry. But the revolution was not complete until the mathematical world took no ...
STRAND F: GEOMETRY F1 Angles and Symmetry Text
... Shapes have line symmetry if a mirror could be placed so that one side is an exact reflection of the other. These imaginary 'mirror lines' are shown by dotted lines in the diagrams below. ...
... Shapes have line symmetry if a mirror could be placed so that one side is an exact reflection of the other. These imaginary 'mirror lines' are shown by dotted lines in the diagrams below. ...
Mirror symmetry (string theory)
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.Mirror symmetry was originally discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously.Today mirror symmetry is a major research topic in pure mathematics, and mathematicians are working to develop a mathematical understanding of the relationship based on physicists' intuition. Mirror symmetry is also a fundamental tool for doing calculations in string theory, and it has been used to understand aspects of quantum field theory, the formalism that physicists use to describe elementary particles. Major approaches to mirror symmetry include the homological mirror symmetry program of Maxim Kontsevich and the SYZ conjecture of Andrew Strominger, Shing-Tung Yau, and Eric Zaslow.