Parallel postulates and continuity axioms: a mechanized study in
... further away from A than D on the half line AD, one can build a line which goes through T and intersects the sides BA and BC of the angle ∠ABC respectively further away from B than A and C (Fig. 13). 2. The second postulate that we will study in this paper was adopted by Hilbert in [Hil60] and is kn ...
... further away from A than D on the half line AD, one can build a line which goes through T and intersects the sides BA and BC of the angle ∠ABC respectively further away from B than A and C (Fig. 13). 2. The second postulate that we will study in this paper was adopted by Hilbert in [Hil60] and is kn ...
Solutions and Notes for Supplementary Problems
... Using (1) and also the segments marked in figure 347a, we see that (α + p + q) + (γ + r + s) = (δ + p + s) + (β + q + r). But α + p + q = α0 , since they are the two common external tangents of circles S1 , S2 . And γ + r + s = γ 0 , since they are the common external tangents of circles S3 , S4 . S ...
... Using (1) and also the segments marked in figure 347a, we see that (α + p + q) + (γ + r + s) = (δ + p + s) + (β + q + r). But α + p + q = α0 , since they are the two common external tangents of circles S1 , S2 . And γ + r + s = γ 0 , since they are the common external tangents of circles S3 , S4 . S ...
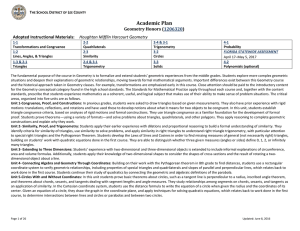
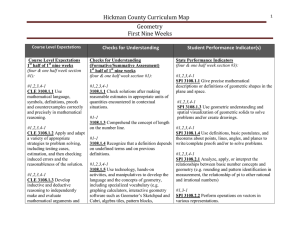
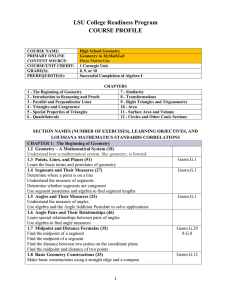
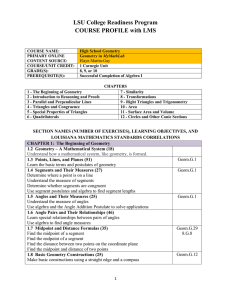
Geometry with Computers
... been unimaginably powerful 20 years ago. These machines can help visualize geometric results in a dynamic manner that is far more compelling than the fixed drawings appearing in standard mathematics books or that can be produced with pencil and paper. This book comes with a computer program called G ...
... been unimaginably powerful 20 years ago. These machines can help visualize geometric results in a dynamic manner that is far more compelling than the fixed drawings appearing in standard mathematics books or that can be produced with pencil and paper. This book comes with a computer program called G ...
Content, Methods, and Context of the Theory of Parallels
... critical acumen, was just as faulty as those he had criticized. We have flawed proofs by Aghanis (5th century) and Simplicius (6th-century), two Byzantine scholars. Many others by medieval Islamic mathematicians have survived, including attempts by al-Jawhari and Thabit ibn Qurra in the 9th century, ...
... critical acumen, was just as faulty as those he had criticized. We have flawed proofs by Aghanis (5th century) and Simplicius (6th-century), two Byzantine scholars. Many others by medieval Islamic mathematicians have survived, including attempts by al-Jawhari and Thabit ibn Qurra in the 9th century, ...
Ways to Prove that Quadrilaterals are Parallelograms
... Four theorems are presented in this lesson that can be used to show that a quadrilateral is a parallelogram. ...
... Four theorems are presented in this lesson that can be used to show that a quadrilateral is a parallelogram. ...
Coaching Class Hara 8.Quadrilaterals A Diagonal Of A
... What can we say about the converse of this property? Is the converse also true? Yes, the converse of this property is also true. It can be stated as follows. ...
... What can we say about the converse of this property? Is the converse also true? Yes, the converse of this property is also true. It can be stated as follows. ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.