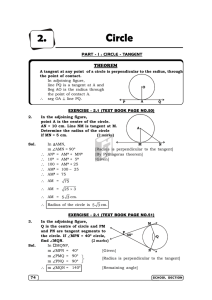
Circle - mt-iconnect.com
... two concentric circles are given and line AB is tangent to the smaller O circle at T. Show that T is the (2 marks) midpoint of seg AB. Construction : Let O be the centre of the B A ...
... two concentric circles are given and line AB is tangent to the smaller O circle at T. Show that T is the (2 marks) midpoint of seg AB. Construction : Let O be the centre of the B A ...
Constructive Geometry and the Parallel Postulate
... prove that for every p and L, there exists a perpendicular to L through p, then we must give a single, “uniform” ruler-and-compass construction that works for any p, whether or not p is on L. Readers new to constructive mathematics may not understand why an argument by cases is not allowed. Let me e ...
... prove that for every p and L, there exists a perpendicular to L through p, then we must give a single, “uniform” ruler-and-compass construction that works for any p, whether or not p is on L. Readers new to constructive mathematics may not understand why an argument by cases is not allowed. Let me e ...
Parallelograms II 17 - e
... • Now complete the quadrilateral ABCD as shown above. • Check whether the sides AB and DC as well as the sides BC and AD in the quadrilateral ABCD are parallel to each other by using a set square and a ruler or by measuring a pair of alternate angles. Accordingly, it can be seen that if the diagonal ...
... • Now complete the quadrilateral ABCD as shown above. • Check whether the sides AB and DC as well as the sides BC and AD in the quadrilateral ABCD are parallel to each other by using a set square and a ruler or by measuring a pair of alternate angles. Accordingly, it can be seen that if the diagonal ...
high speed cordic design for fixed angle of rotation
... algorithm has become a widely used approach to elementary function evaluation when the silicon area is a primary constraint. The CORDIC algorithm was developed by J. E. Volder in 1959 for the computation of trigonometric functions. This has been recognized as the best compromise between the table lo ...
... algorithm has become a widely used approach to elementary function evaluation when the silicon area is a primary constraint. The CORDIC algorithm was developed by J. E. Volder in 1959 for the computation of trigonometric functions. This has been recognized as the best compromise between the table lo ...
Lesson
... c) A Pair of Opposite Sides Is Both Parallel and Congruent d) Both Pairs of Opposite Angles Are Congruent e) Diagonals Bisect Each Other ...
... c) A Pair of Opposite Sides Is Both Parallel and Congruent d) Both Pairs of Opposite Angles Are Congruent e) Diagonals Bisect Each Other ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.