three dimensional geometry
... Solution. Direction ratios of the given lines are < 1, – 2, – 2 > and < 0, 2, 1 >. Let < a, b, c > be direction ratios of the line which is perpendicular to the given lines, then a . 1 + b . (– 2) + c . (– 2) = 0 ⇒ a – 2b – 2c = 0 and a . 0 + b . 2 + c . 1 = 0 ⇒ 2b + c = 0 From (ii), we get c = – 2b ...
... Solution. Direction ratios of the given lines are < 1, – 2, – 2 > and < 0, 2, 1 >. Let < a, b, c > be direction ratios of the line which is perpendicular to the given lines, then a . 1 + b . (– 2) + c . (– 2) = 0 ⇒ a – 2b – 2c = 0 and a . 0 + b . 2 + c . 1 = 0 ⇒ 2b + c = 0 From (ii), we get c = – 2b ...
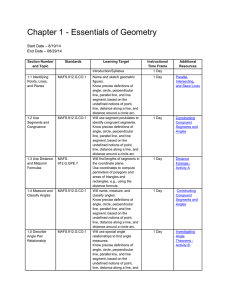
Parallel and Perpendicular Lines
... In this chapter, you will explore the different relationships formed by parallel and perpendicular lines and planes. Different angle relationships will also be explored and what happens when lines are parallel. You will start to prove lines parallel or perpendicular using a fill-in-the-blank 2-colum ...
... In this chapter, you will explore the different relationships formed by parallel and perpendicular lines and planes. Different angle relationships will also be explored and what happens when lines are parallel. You will start to prove lines parallel or perpendicular using a fill-in-the-blank 2-colum ...
3.5 Proving Lines Parallel
... Lines Parallel line are parallel. Since the slots are perpendicular to each of the sides, the slots are parallel. Since any pair of slots is perpendicular the sides, they are also parallel. 30. PROOF Write a paragraph proof of Theorem 3.8. SOLUTION: ...
... Lines Parallel line are parallel. Since the slots are perpendicular to each of the sides, the slots are parallel. Since any pair of slots is perpendicular the sides, they are also parallel. 30. PROOF Write a paragraph proof of Theorem 3.8. SOLUTION: ...
CHAPTER 3 Parallel and Perpendicular Lines
... To see a demonstration of this construction, go to: http://www.mathsisfun.com/geometry/construct-perpnotline.htm l Investigation 3-3: Perpendicular Line Construction; through a Point on the Line (an internal point) 1. Draw a horizontal line and a point on that line. Label the line l and the point A. ...
... To see a demonstration of this construction, go to: http://www.mathsisfun.com/geometry/construct-perpnotline.htm l Investigation 3-3: Perpendicular Line Construction; through a Point on the Line (an internal point) 1. Draw a horizontal line and a point on that line. Label the line l and the point A. ...
Parallel Lines Cut by Transversal Lesson PP
... If two parallel lines are intersected by a transversal, • the acute angles that are formed are all congruent, • the obtuse angles are all congruent, • and any acute angle is supplementary to any obtuse angle. If the transversal is perpendicular to the parallel lines, all angles are 90°. ...
... If two parallel lines are intersected by a transversal, • the acute angles that are formed are all congruent, • the obtuse angles are all congruent, • and any acute angle is supplementary to any obtuse angle. If the transversal is perpendicular to the parallel lines, all angles are 90°. ...
Angles and Parallel Lines
... Consecutive Interior Angles Theorem – If two parallel lines are cut by a transversal, then each pair of consecutive interior angles is supplementary (sum to 180o). You will prove this theorem as a homework problem! ...
... Consecutive Interior Angles Theorem – If two parallel lines are cut by a transversal, then each pair of consecutive interior angles is supplementary (sum to 180o). You will prove this theorem as a homework problem! ...
Geometry Module 1, Topic G, Overview
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. ...
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. ...
Geometry Module 1, Topic G, Overview
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. ...
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. ...
Is it As Parallelogram?
... By Reflexive and AAS, these two triangles are congruent, so their corresponding sides will be congruent by CPCTC. This means the left and right sides are congruent and the top and bottom are congruent. (other reasons work too) ...
... By Reflexive and AAS, these two triangles are congruent, so their corresponding sides will be congruent by CPCTC. This means the left and right sides are congruent and the top and bottom are congruent. (other reasons work too) ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.