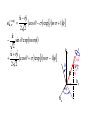Download Localized - Current research interest: photon position

Localized Photon States
Here be dragons
Margaret Hawton
Lakehead University
Thunder Bay, Canada
Introduction
In standard quantum mechanics a measurement is
associated with an operator and collapse to one of its
eigenvectors. For the position observable this requires a
position operator and collapse to a localized state.
The generalized theory of observables only requires a
partition of the identity operator, i.e. a positive operator
valued measure (POVM). I will show here that the
elements the POVM of a photon counting array detector
are projectors onto localized photon states.
Since the early days of quantum mechanics it has been
believed that there is no photon position operator with
localized eigenvectors.
The emergence of localized photon states as the POVM of
a photon counting array sheds light on this long standing
problem. By using the generalized theory of observables
many of the theoretical difficulties are avoided.
Recently Tsang [Phys. Rev. Lett. 102, 253601 (2009)]
defined a similar photon position POVM consisting of
projectors onto localized states and applied it to a new
quantum imaging method.
Outline
Localized electron and photon states
POVM of a photon counting array
Hegerfeldt theorem and scattering
Conclude
Localized basis for nonrelativistic electron
1
The position eigenvector, r 
V
 exp ik  r ,
k
is a -function in coordinate space. This 
energy fiction describes localization in a small
region.
k k '   k ,k ' implies r r'   r  r'.
An electron has spin AM s parallel to the arbitrary zaxis where s=½. The position/spin basis
r, s is complete, i.e. 1̂    d 3r r, s r, s .
s
The following has been proved regarding photon
position:
(1) The relationship between the electric/magnetic field
and photon number amplitude is nonlocal in r-space.
(2) There are no definite s, l=0 localized photon states
(Newton and Wigner 1949) and no photon position
operator with localized eigenvectors that transforms like
a vector.
(3) If a relativistic particle is localized for an instant, at
all other times it is not confined to any bounded region
(Hegerfeldt 1974).
This does not exclude localized photon states with the
following properties:
(1) While the probability of absorption by an atom
^ (+)|2>, I will show here that photon counting by a
<|E
thick detector is described by photon number density.
(2) Helicity and total AM can have definite values,
but spin cannot. Their nonintegrable AM leads to the
Berry phase observed in helically wound fibers.
(3) Incoming and outgoing waves are equally likely.
Localization is due to destructive interference of
these counterpropagating waves.
Photon annihilation and creation operators
In the IP the positive energy QED electric field operator
ˆ (  ) r, t   i 
E

k
kc
ek , aˆk , exp ik  r  ikct 
2 0V
annihilates the field due to a photon at r
while the photon number amplitude operator
1
aˆ r, t  
aˆk , exp ik  r  ikct 

V k
annihilates a photon at r.
^a(r,t) creates a localized photon while ^E(-)(r,t) creates
its nonlocal field.
Localized photon states
The localized states,
r, t ,  aˆ r, t  vac ,
are orthonormal, i.e.
r, t , r' , t , '   r  r' , '
and form a partition of the identity operator,
1̂ 
3
d
  r r, t ,  r, t ,  .
  1
Photon number amplitude and field operators differ
by k  constant. Both require transverse unit
vectors ek, for helicities =1 and all k.
(2) The transverse unit vectors
in k-space spherical polar coordinates are
ek ,


1 ˆ
ˆ exp  i  ,  

θ  iφ
2
where  is the Euler angle and helicity
 is internal AM parallel to k. These
unit vectors have definite helicity and
total AM but no definite spin.
kz
φ̂


k

θ̂
ky
kx
The choice =- gives j= and the total AM is  . The
k’s close to the +z-direction needed to describe a
paraxial beam have spin s= and l=0 so all orbital AM
is in |>, not the basis.
The sketch shows =+1 E and B and wave fronts for kcomponents of a localized state close to +z and –z. For
the latter, s=-1 so l=2 is required to give j=1.
(3) In+Out: We don’t know if a component plane wave
is approaching or leaving the point of localization.
e
i ( k r  kct )
The t=0 localized state is a sum of incoming and
outgoing spherical shells. More details later in II.
f (r  ct )
f (r  ct )
Position measurement will be discussed from two
perspectives:
^z
I. The POVM of a photon counting array detector and
its relationship to photon density.
II. The Hegerfeldt theorem, counterpropagating waves,
and scattering of a photon by a nanoparticle.
I. POVM of a photon counting array
When measuring photon position using a photon
counting array the photons are the particles of interest
and the detector atoms form an ancillary Hilbert
subspace. The POVM is the partial trace over the
atom subspace.
The measurement consists of counting the e-h pairs
created in each pixel. For simplicity it will be assumed
here that 1 photon is counted, but 2 photons is treated
in [1]: Hawton, Phys. Rev. A 82, 012117 (2010).
It will be assumed that each atom has a ground state
|g> and 3 mutually orthogonal excited states, |er,p>.
The IP or SP 1-photon counting operator checks for an
excited atom in the nth pixel by projecting onto one of
these excited states using
SP
ˆ
F1,n 
e
p ,rDn
r, p
er , p
where Dn denotes the nth pixel of the array.
To incorporate the dynamics into the counting
operator we can transform to the HP using the usual
E interaction Hamiltonian,
IP
ˆ
H I r, t   μ 
()
ˆ
 E p r, t  er, p t  g .
p ,rV
This operator promotes an atom from the ground
state to an excited state while annihilating a photon.
We can choose p for normal incidence in the
paraxial approximation.
Transformation requires the unitary operator
 i t

IP
Uˆ t   exp   dt ' Hˆ I t' 
  t0

where the first order term
t
i
(1)
ˆ
U t     dt ' Hˆ IIP t' 
 t0
gives the 1-photon counting operator
HP
(1)
IP ˆ (1)
ˆ
ˆ
ˆ
F1,n t   U t F1,n U t .
Writing out the unitary and counting operators for a
measurement performed between t0 and t0+t
t0  t
i
(1)
ˆ
U t0  t     dt ' μ   Eˆ (p ) r, t ' er , p g
 t0
p ,rV
Fˆ HP t0   Uˆ (1) t0  t   er ', p ' er ', p ' Uˆ (1) t0  t 
p ',r 'Dn
the (Glauber) counting operator becomes
2
2

HP
ˆ
F1,n t0  

t 0  t
( )
()
ˆ
ˆ
  dt  E p r, t E p r, t  g g .
t0
p ,rDn
A photon counting detector should be thick enough
to absorb all photons incident on it. We can change
3
the sum over atoms to an integral using  r  a  d r.
For a single mode with kz=nk+iak the absorptivity is
 2  a
1 kc 2 2
ak 

a 
kc.
2 2 0

2 0
Integration of exp(-2akz) over detector thickness gives
1/2ak that eliminates the k’s in E(-) E(+). In [1],
following Bondurant 1985, this was proved for a sum
over modes to first order in  k  k  k0  / k0 .
The trace over the ancillary atom states eliminates the
factor |g><g| to give the POVM
Pˆ1,n t0   c

t0  t
 dt  dxdy r, t ,
t0
r, t ,  .
pixel
This is an integral over projectors onto the
localized states!
For an initial and HP photon state |> the probability
to count a photon is
t 0  t
 | Pˆ t  |   c
dt dxdy
1, n
0



t0

pixel
  | r, t ,  r, t ,  |  .
Position information is obtained by projection of the
QED state vector onto the localized states,
  r, t   r, t ,  |
and the probability to count a photon equals an
integral over it’s absolute square, i.e.
 | Pˆ1,n t0  |   c

t 0  t
 dt  dxdy   r, t 
t0
pixel
Only modes present in |> contribute to (r,t).
2
.
II. Hegerfeldt theorem and scattering
ct
If a particle is confined to the red
region at t=0 it is not confined to a
sphere of radius ct at other time t.
This could lead to causality
violations.
The Hegerfeldt theorem doesn’t apply to photon counting
since no localized photon state is created, but a scattered
photon is not annihilated, at least not permanently, so it
might apply to scattering. Next I’ll consider how this
relates to exactly localized states, k exp ik  r  kct / V .
Exact (-function) localization: The real and imaginary
parts of r,t, 0,0, can’t be localized simultaneously for
arbitrary t since the sum over cos[k(rct)] gives functions but isin[k(r  ct)] gives i/(r  ct) tails.
r,t ,  0,0, 
t<0
c
-function
t>0
c
r
Nonlocal tail
r=0
  r,0  r,0, 0,0, 
r
Only at t=0 does destructive interference completely
eliminate the nonlocal tails leaving just a -function.
Hegerfeldt proved that generalization to localization in a
finite region doesn’t change this property. Destructive
interference explains the physics behind his theorem.
Scattering: In Celebrano et al [Optics Express 18, 13829
(2010)] a one-photon pulse is focused onto a nanoparticle
and scattered onto a detector. Photon localization is
achieved by focusing with a microscope objective.
detector
1-photon input,
nanoparticle
In+Out pulses

Zumofen et al [Phys. Rev. Lett. 101, 180404 (2008)]
predicts up to 100% reflection and 55% was achieved
in the experiment. Wavelength is 589nm and the
nanoparticles are smaller, 46x94nm.
Many wave vectors, both in and out, are present. This
approaches a physical realization of a localized state.
Conclusion
Localized photon states with definite total AM exist due to
destructive interference of in/out pulses.
A photon counting array measures coarse grained photon
number density but ‘collapse’ is to the vacuum state.
This photon number density equals the absolute square of
the projection of the photon state vector onto the localized
basis.
Localized states can exist in a scattering experiment.
e
(  m )
k ,
xˆ  iyˆ
cos    exp im  1 

2 2
zˆ

sin  exp im 
2
xˆ  iyˆ
cos    exp im  1 

2 2
kz
φ̂


k

kx
θ̂
ky