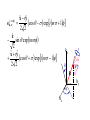* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Localized - Current research interest: photon position
Electron configuration wikipedia , lookup
Coupled cluster wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Atomic theory wikipedia , lookup
Quantum state wikipedia , lookup
Bell test experiments wikipedia , lookup
Elementary particle wikipedia , lookup
Path integral formulation wikipedia , lookup
Canonical quantization wikipedia , lookup
Bra–ket notation wikipedia , lookup
EPR paradox wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Bremsstrahlung wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
History of quantum field theory wikipedia , lookup
Bell's theorem wikipedia , lookup
Renormalization wikipedia , lookup
Compact operator on Hilbert space wikipedia , lookup
Self-adjoint operator wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Franck–Condon principle wikipedia , lookup
Probability amplitude wikipedia , lookup
Coherent states wikipedia , lookup
Wave–particle duality wikipedia , lookup
Density matrix wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Double-slit experiment wikipedia , lookup
Quantum key distribution wikipedia , lookup
Electron scattering wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Localized Photon States Here be dragons Margaret Hawton Lakehead University Thunder Bay, Canada Introduction In standard quantum mechanics a measurement is associated with an operator and collapse to one of its eigenvectors. For the position observable this requires a position operator and collapse to a localized state. The generalized theory of observables only requires a partition of the identity operator, i.e. a positive operator valued measure (POVM). I will show here that the elements the POVM of a photon counting array detector are projectors onto localized photon states. Since the early days of quantum mechanics it has been believed that there is no photon position operator with localized eigenvectors. The emergence of localized photon states as the POVM of a photon counting array sheds light on this long standing problem. By using the generalized theory of observables many of the theoretical difficulties are avoided. Recently Tsang [Phys. Rev. Lett. 102, 253601 (2009)] defined a similar photon position POVM consisting of projectors onto localized states and applied it to a new quantum imaging method. Outline Localized electron and photon states POVM of a photon counting array Hegerfeldt theorem and scattering Conclude Localized basis for nonrelativistic electron 1 The position eigenvector, r V exp ik r , k is a -function in coordinate space. This energy fiction describes localization in a small region. k k ' k ,k ' implies r r' r r'. An electron has spin AM s parallel to the arbitrary zaxis where s=½. The position/spin basis r, s is complete, i.e. 1̂ d 3r r, s r, s . s The following has been proved regarding photon position: (1) The relationship between the electric/magnetic field and photon number amplitude is nonlocal in r-space. (2) There are no definite s, l=0 localized photon states (Newton and Wigner 1949) and no photon position operator with localized eigenvectors that transforms like a vector. (3) If a relativistic particle is localized for an instant, at all other times it is not confined to any bounded region (Hegerfeldt 1974). This does not exclude localized photon states with the following properties: (1) While the probability of absorption by an atom ^ (+)|2>, I will show here that photon counting by a <|E thick detector is described by photon number density. (2) Helicity and total AM can have definite values, but spin cannot. Their nonintegrable AM leads to the Berry phase observed in helically wound fibers. (3) Incoming and outgoing waves are equally likely. Localization is due to destructive interference of these counterpropagating waves. Photon annihilation and creation operators In the IP the positive energy QED electric field operator ˆ ( ) r, t i E k kc ek , aˆk , exp ik r ikct 2 0V annihilates the field due to a photon at r while the photon number amplitude operator 1 aˆ r, t aˆk , exp ik r ikct V k annihilates a photon at r. ^a(r,t) creates a localized photon while ^E(-)(r,t) creates its nonlocal field. Localized photon states The localized states, r, t , aˆ r, t vac , are orthonormal, i.e. r, t , r' , t , ' r r' , ' and form a partition of the identity operator, 1̂ 3 d r r, t , r, t , . 1 Photon number amplitude and field operators differ by k constant. Both require transverse unit vectors ek, for helicities =1 and all k. (2) The transverse unit vectors in k-space spherical polar coordinates are ek , 1 ˆ ˆ exp i , θ iφ 2 where is the Euler angle and helicity is internal AM parallel to k. These unit vectors have definite helicity and total AM but no definite spin. kz φ̂ k θ̂ ky kx The choice =- gives j= and the total AM is . The k’s close to the +z-direction needed to describe a paraxial beam have spin s= and l=0 so all orbital AM is in |>, not the basis. The sketch shows =+1 E and B and wave fronts for kcomponents of a localized state close to +z and –z. For the latter, s=-1 so l=2 is required to give j=1. (3) In+Out: We don’t know if a component plane wave is approaching or leaving the point of localization. e i ( k r kct ) The t=0 localized state is a sum of incoming and outgoing spherical shells. More details later in II. f (r ct ) f (r ct ) Position measurement will be discussed from two perspectives: ^z I. The POVM of a photon counting array detector and its relationship to photon density. II. The Hegerfeldt theorem, counterpropagating waves, and scattering of a photon by a nanoparticle. I. POVM of a photon counting array When measuring photon position using a photon counting array the photons are the particles of interest and the detector atoms form an ancillary Hilbert subspace. The POVM is the partial trace over the atom subspace. The measurement consists of counting the e-h pairs created in each pixel. For simplicity it will be assumed here that 1 photon is counted, but 2 photons is treated in [1]: Hawton, Phys. Rev. A 82, 012117 (2010). It will be assumed that each atom has a ground state |g> and 3 mutually orthogonal excited states, |er,p>. The IP or SP 1-photon counting operator checks for an excited atom in the nth pixel by projecting onto one of these excited states using SP ˆ F1,n e p ,rDn r, p er , p where Dn denotes the nth pixel of the array. To incorporate the dynamics into the counting operator we can transform to the HP using the usual E interaction Hamiltonian, IP ˆ H I r, t μ () ˆ E p r, t er, p t g . p ,rV This operator promotes an atom from the ground state to an excited state while annihilating a photon. We can choose p for normal incidence in the paraxial approximation. Transformation requires the unitary operator i t IP Uˆ t exp dt ' Hˆ I t' t0 where the first order term t i (1) ˆ U t dt ' Hˆ IIP t' t0 gives the 1-photon counting operator HP (1) IP ˆ (1) ˆ ˆ ˆ F1,n t U t F1,n U t . Writing out the unitary and counting operators for a measurement performed between t0 and t0+t t0 t i (1) ˆ U t0 t dt ' μ Eˆ (p ) r, t ' er , p g t0 p ,rV Fˆ HP t0 Uˆ (1) t0 t er ', p ' er ', p ' Uˆ (1) t0 t p ',r 'Dn the (Glauber) counting operator becomes 2 2 HP ˆ F1,n t0 t 0 t ( ) () ˆ ˆ dt E p r, t E p r, t g g . t0 p ,rDn A photon counting detector should be thick enough to absorb all photons incident on it. We can change 3 the sum over atoms to an integral using r a d r. For a single mode with kz=nk+iak the absorptivity is 2 a 1 kc 2 2 ak a kc. 2 2 0 2 0 Integration of exp(-2akz) over detector thickness gives 1/2ak that eliminates the k’s in E(-) E(+). In [1], following Bondurant 1985, this was proved for a sum over modes to first order in k k k0 / k0 . The trace over the ancillary atom states eliminates the factor |g><g| to give the POVM Pˆ1,n t0 c t0 t dt dxdy r, t , t0 r, t , . pixel This is an integral over projectors onto the localized states! For an initial and HP photon state |> the probability to count a photon is t 0 t | Pˆ t | c dt dxdy 1, n 0 t0 pixel | r, t , r, t , | . Position information is obtained by projection of the QED state vector onto the localized states, r, t r, t , | and the probability to count a photon equals an integral over it’s absolute square, i.e. | Pˆ1,n t0 | c t 0 t dt dxdy r, t t0 pixel Only modes present in |> contribute to (r,t). 2 . II. Hegerfeldt theorem and scattering ct If a particle is confined to the red region at t=0 it is not confined to a sphere of radius ct at other time t. This could lead to causality violations. The Hegerfeldt theorem doesn’t apply to photon counting since no localized photon state is created, but a scattered photon is not annihilated, at least not permanently, so it might apply to scattering. Next I’ll consider how this relates to exactly localized states, k exp ik r kct / V . Exact (-function) localization: The real and imaginary parts of r,t, 0,0, can’t be localized simultaneously for arbitrary t since the sum over cos[k(rct)] gives functions but isin[k(r ct)] gives i/(r ct) tails. r,t , 0,0, t<0 c -function t>0 c r Nonlocal tail r=0 r,0 r,0, 0,0, r Only at t=0 does destructive interference completely eliminate the nonlocal tails leaving just a -function. Hegerfeldt proved that generalization to localization in a finite region doesn’t change this property. Destructive interference explains the physics behind his theorem. Scattering: In Celebrano et al [Optics Express 18, 13829 (2010)] a one-photon pulse is focused onto a nanoparticle and scattered onto a detector. Photon localization is achieved by focusing with a microscope objective. detector 1-photon input, nanoparticle In+Out pulses Zumofen et al [Phys. Rev. Lett. 101, 180404 (2008)] predicts up to 100% reflection and 55% was achieved in the experiment. Wavelength is 589nm and the nanoparticles are smaller, 46x94nm. Many wave vectors, both in and out, are present. This approaches a physical realization of a localized state. Conclusion Localized photon states with definite total AM exist due to destructive interference of in/out pulses. A photon counting array measures coarse grained photon number density but ‘collapse’ is to the vacuum state. This photon number density equals the absolute square of the projection of the photon state vector onto the localized basis. Localized states can exist in a scattering experiment. e ( m ) k , xˆ iyˆ cos exp im 1 2 2 zˆ sin exp im 2 xˆ iyˆ cos exp im 1 2 2 kz φ̂ k kx θ̂ ky