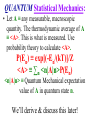Download Statistical Physics Overview

Introduction to Statistical
& Thermal Physics
Basic Definitions & Terminology
Thermodynamics (“Thermo”)
is a macroscopic theory!
• Thermo ≡ The study of the
Macroscopic properties of
systems based on a few laws &
hypotheses. It results in
The Laws of Thermodynamics!
Thermodynamics (“Thermo”)
1. Derives relations between the
macroscopic, measureable
properties (& parameters) of a
system (heat capacity, temperature,
volume, pressure, ..).
2. Makes NO direct reference to the
microscopic structure of matter.
Thermo: Makes NO direct reference to
the microscopic structure of matter.
For example, from thermo, we can
derive that, for an ideal gas, the heat
capacities are related by
Cp– Cv = R.
But, thermo gives no prescription for
calculating numerical values for Cp, Cv.
Calculating these requires a microscopic
model & statistical mechanics.
Kinetic Theory is a microscopic theory!
(Boltzmann, Maxwell & others in the 19th Century)
1. It applies the Laws of Mechanics (Classical
or Quantum) to a microscopic model of the
individual molecules of a system.
2. It allows the calculation of various
Macroscopically measurable quantities on
the basis of a Microscopic theory applied to
a model of the system.
– For example, it might be able to calculate the specific
heat Cv using Newton’s 2nd Law along with the
known force laws between the particles that make up
the substance of interest.
Kinetic Theory is a
microscopic theory!
3. It uses the microscopic equations
of motion for individual particles.
4. It uses the methods of Probability
& Statistics & the equations of
motion of the particles to calculate
the (thermal average) Macroscopic
properties of a substance.
Statistical Mechanics
(or Statistical Thermodynamics)
1. Ignores a detailed consideration of
molecules as individuals.
2. Is a Microscopic, statistical approach
to calculation of Macroscopic quantities.
3. Applies the methods of Probability &
Statistics to Macroscopic systems with
HUGE numbers of particles.
Statistical Mechanics
3. For systems with known energy
(Classical or Quantum) it gives
BOTH
A. Relations between Macroscopic
quantities (like Thermo)
AND
B. NUMERICAL VALUES of
them (like Kinetic Theory).
This course covers all three!
1. Thermodynamics
2. Kinetic Theory
3. Statistical Mechanics
Statistical Mechanics:
Reproduces ALL of Thermodynamics
& ALL of Kinetic Theory.
It is more general than either!
A Hierarchy of Theories
(of Systems with a Huge Number of Particles)
Statistical Mechanics
(the most general theory)
___________|__________
|
|
|
|
|
|
Thermodynamics
Kinetic Theory
(a general, macroscopic theory)
(a microscopic theory most
easily applicable to gases)
Remarks on Statistical & Thermal Physics
A brief overview of Statistical Mechanics.
General overview. No worry about details now!
The Key Principle of CLASSICAL
Statistical Mechanics is as follows:
• Consider a system containing N particles with 3d
positions r1,r2,r3,…rN, & momenta p1,p2,p3,…pN. The
system is in Thermal Equilibrium at absolute
temperature T. We’ll show that the probability of the
system having energy E is:
Note: The Canonical
Ensemble is assumed!!
P(E) ≡ e[-E/(kT)]/Z
Z ≡ “Partition Function”, T ≡ Absolute
Temperature, k ≡ Boltzmann’s Constant
The Classsical Partition Function
Z ≡ ∫∫∫d3r1d3r2…d3rN d3p1d3p2…d3pN e(-E/kT)
 A 6N Dimensional Integral!
• This assumes that we have already solved
the classical mechanics problem for each
particle in the system so that we know the
total energy E for the N particles as a
function of all positions ri & momenta pi.
E = E(r1,r2,r3,…rN,p1,p2,p3,…pN)D
We’ll derive & discuss this later!
CLASSICAL Statistical Mechanics:
• Let A ≡ any measurable, macroscopic
quantity. The thermodynamic average of A
≡ <A>. This is what is measured. Use
probability theory to calculate <A> :
P(E) ≡
[-E/(kT)]
e
/Z
<A>≡ ∫∫∫(A)d3r1d3r2…d3rN d3p1d3p2…d3pNP(E)
 Another 6N Dimensional Integral!
We’ll derive & discuss this later!
The Key Principle of QUANTUM
Statistical Mechanics is as follows:
• Consider a system which can be in any one of
N quantum states. The system is in Thermal
Equilibrium at absolute temperature T. We’ll
show that the probability of the system being
in state n with energy En is: Note: The Canonical
P(En) ≡ exp[-En/(kT)]/Z
Z ≡ “Partition Function”
T ≡ Absolute Temperature
k ≡ Boltzmann’s Constant
Ensemble is assumed!!
The Quantum Mechanical
Partition Function
Z ≡ ∑nexp[-En/(kT)]
We’ll derive & discuss this later!
QUANTUM Statistical Mechanics:
• Let A ≡ any measurable, macroscopic
quantity. The thermodynamic average of A
≡ <A>. This is what is measured. Use
probability theory to calculate <A>.
P(En) ≡ exp[(-En/(kT)]/Z
<A> ≡ ∑n <n|A|n>P(En)
<n|A|n> ≡ Quantum Mechanical expectation
value of A in quantum state n.
We’ll derive & discuss this later!
• The point of showing this is that Classical &
Quantum Statistical Mechanics both revolve
around the calculation of P(E) or P(En).
• To calculate the probability distribution, we need
to calculate the Partition Function Z (similar in
the classical & quantum cases).
Quoting Richard P. Feynman*:
“P(E) & Z are at the summit of both
Classical & Quantum
Statistical Mechanics.”
*
From “Statistical Mechanics”
by R.P. Feynman, (W.A. Benjamin, 1972)
Statistical Mechanics
(Classical or Quantum)
P(E), Z
Equations of
Motion
Calculation of
Measurable
Quantities
The Statistical/Thermal
Physics “Mountain”
P(E), Z
Equations of
Motion
Calculation of
Measurable
Quantities
Statistical/Thermal Physics “Mountain”
• The entire subject is either the “climb” UP to the
summit (calculation of P(E), Z) or the slide DOWN
(use of P(E), Z to calculate measurable properties).
• On the way UP: Thermal Equilibrium &
Temperature are defined from statistics. On the way
DOWN, all of Thermodynamics can be derived,
beginning with microscopic theory.