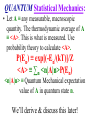* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Statistical Physics Overview
Density matrix wikipedia , lookup
Quantum field theory wikipedia , lookup
Atomic theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Ensemble interpretation wikipedia , lookup
Identical particles wikipedia , lookup
Bell's theorem wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Double-slit experiment wikipedia , lookup
Wave–particle duality wikipedia , lookup
Probability amplitude wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Renormalization wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum state wikipedia , lookup
Scalar field theory wikipedia , lookup
EPR paradox wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
History of quantum field theory wikipedia , lookup
Path integral formulation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Canonical quantization wikipedia , lookup
Introduction to Statistical & Thermal Physics Basic Definitions & Terminology Thermodynamics (“Thermo”) is a macroscopic theory! • Thermo ≡ The study of the Macroscopic properties of systems based on a few laws & hypotheses. It results in The Laws of Thermodynamics! Thermodynamics (“Thermo”) 1. Derives relations between the macroscopic, measureable properties (& parameters) of a system (heat capacity, temperature, volume, pressure, ..). 2. Makes NO direct reference to the microscopic structure of matter. Thermo: Makes NO direct reference to the microscopic structure of matter. For example, from thermo, we can derive that, for an ideal gas, the heat capacities are related by Cp– Cv = R. But, thermo gives no prescription for calculating numerical values for Cp, Cv. Calculating these requires a microscopic model & statistical mechanics. Kinetic Theory is a microscopic theory! (Boltzmann, Maxwell & others in the 19th Century) 1. It applies the Laws of Mechanics (Classical or Quantum) to a microscopic model of the individual molecules of a system. 2. It allows the calculation of various Macroscopically measurable quantities on the basis of a Microscopic theory applied to a model of the system. – For example, it might be able to calculate the specific heat Cv using Newton’s 2nd Law along with the known force laws between the particles that make up the substance of interest. Kinetic Theory is a microscopic theory! 3. It uses the microscopic equations of motion for individual particles. 4. It uses the methods of Probability & Statistics & the equations of motion of the particles to calculate the (thermal average) Macroscopic properties of a substance. Statistical Mechanics (or Statistical Thermodynamics) 1. Ignores a detailed consideration of molecules as individuals. 2. Is a Microscopic, statistical approach to calculation of Macroscopic quantities. 3. Applies the methods of Probability & Statistics to Macroscopic systems with HUGE numbers of particles. Statistical Mechanics 3. For systems with known energy (Classical or Quantum) it gives BOTH A. Relations between Macroscopic quantities (like Thermo) AND B. NUMERICAL VALUES of them (like Kinetic Theory). This course covers all three! 1. Thermodynamics 2. Kinetic Theory 3. Statistical Mechanics Statistical Mechanics: Reproduces ALL of Thermodynamics & ALL of Kinetic Theory. It is more general than either! A Hierarchy of Theories (of Systems with a Huge Number of Particles) Statistical Mechanics (the most general theory) ___________|__________ | | | | | | Thermodynamics Kinetic Theory (a general, macroscopic theory) (a microscopic theory most easily applicable to gases) Remarks on Statistical & Thermal Physics A brief overview of Statistical Mechanics. General overview. No worry about details now! The Key Principle of CLASSICAL Statistical Mechanics is as follows: • Consider a system containing N particles with 3d positions r1,r2,r3,…rN, & momenta p1,p2,p3,…pN. The system is in Thermal Equilibrium at absolute temperature T. We’ll show that the probability of the system having energy E is: Note: The Canonical Ensemble is assumed!! P(E) ≡ e[-E/(kT)]/Z Z ≡ “Partition Function”, T ≡ Absolute Temperature, k ≡ Boltzmann’s Constant The Classsical Partition Function Z ≡ ∫∫∫d3r1d3r2…d3rN d3p1d3p2…d3pN e(-E/kT) A 6N Dimensional Integral! • This assumes that we have already solved the classical mechanics problem for each particle in the system so that we know the total energy E for the N particles as a function of all positions ri & momenta pi. E = E(r1,r2,r3,…rN,p1,p2,p3,…pN)D We’ll derive & discuss this later! CLASSICAL Statistical Mechanics: • Let A ≡ any measurable, macroscopic quantity. The thermodynamic average of A ≡ <A>. This is what is measured. Use probability theory to calculate <A> : P(E) ≡ [-E/(kT)] e /Z <A>≡ ∫∫∫(A)d3r1d3r2…d3rN d3p1d3p2…d3pNP(E) Another 6N Dimensional Integral! We’ll derive & discuss this later! The Key Principle of QUANTUM Statistical Mechanics is as follows: • Consider a system which can be in any one of N quantum states. The system is in Thermal Equilibrium at absolute temperature T. We’ll show that the probability of the system being in state n with energy En is: Note: The Canonical P(En) ≡ exp[-En/(kT)]/Z Z ≡ “Partition Function” T ≡ Absolute Temperature k ≡ Boltzmann’s Constant Ensemble is assumed!! The Quantum Mechanical Partition Function Z ≡ ∑nexp[-En/(kT)] We’ll derive & discuss this later! QUANTUM Statistical Mechanics: • Let A ≡ any measurable, macroscopic quantity. The thermodynamic average of A ≡ <A>. This is what is measured. Use probability theory to calculate <A>. P(En) ≡ exp[(-En/(kT)]/Z <A> ≡ ∑n <n|A|n>P(En) <n|A|n> ≡ Quantum Mechanical expectation value of A in quantum state n. We’ll derive & discuss this later! • The point of showing this is that Classical & Quantum Statistical Mechanics both revolve around the calculation of P(E) or P(En). • To calculate the probability distribution, we need to calculate the Partition Function Z (similar in the classical & quantum cases). Quoting Richard P. Feynman*: “P(E) & Z are at the summit of both Classical & Quantum Statistical Mechanics.” * From “Statistical Mechanics” by R.P. Feynman, (W.A. Benjamin, 1972) Statistical Mechanics (Classical or Quantum) P(E), Z Equations of Motion Calculation of Measurable Quantities The Statistical/Thermal Physics “Mountain” P(E), Z Equations of Motion Calculation of Measurable Quantities Statistical/Thermal Physics “Mountain” • The entire subject is either the “climb” UP to the summit (calculation of P(E), Z) or the slide DOWN (use of P(E), Z to calculate measurable properties). • On the way UP: Thermal Equilibrium & Temperature are defined from statistics. On the way DOWN, all of Thermodynamics can be derived, beginning with microscopic theory.