Download Comp. Genomics

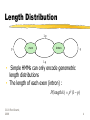
Comp. Genomics
Recitation 9
11/3/06
Gene finding using HMMs &
Conservation
Outline
• Gene finding using HMMs
• Adding trees to HMMs
• phyloHMM
• N-SCAN
• BLAST+ Gene Finding
• SGP2
• Examples
Markov Sequence Models
• Key: distinguish coding/non-coding statistics
• Popular models:
• 6-mers (5th order Markov Model)
• Homogeneous/non-homogeneous (reading frame
specific)
• Not sensitive enough for eukaryote genes: exons too
short, poor detection of splice junctions
3
Length Distribution
1-p
p
exon
intron
q
1-q
• Simple HMMs can only encode genometric
length distributions
• The length of each exon (intron) :
P(length k )  p k (1  p)
CG © Ron Shamir,
2008
4
Exon Length Distribution
• The length distribution of introns is ≈ geometric
• For exons, it isn’t: also affected by splicing
itself:
• Too short (under 50bps): the spliceosomes have no room
• Too long (over 300bps): ends have problems finding each other.
• But as usual there are exceptions.
• A different model for exons is needed
• A different model is needed for exons.
CG © Ron Shamir,
2008
5
Generalized HMM
(Burge & Karlin, J. Mol. Bio. 97 268 78-94)
• Instead of a single char, each state omits a
sequence with some length distribution
CG © Ron Shamir,
2008
6
Generalized HMM
(Burge & Karlin, J. Mol. Bio. 97 268 78-94)
• Overview:
• Hidden Markov states q1,…qn
• State qi has output length distribution fi
• Output of each state can have a separate
probabilistic model (weight matrix model,
HMM…)
• Initial state probability distribution 
• State transition probabilities Tij
CG © Ron Shamir,
2008
7
GenScan Model
CG © Ron Shamir,
2008
Burge & Karlin JMB 97
8
GenScan model
• states = functional units on a gene
• The allowed transitions ensure the order is
biologically consistent.
• As an intron may cut a codon, one must
keep track of the reading frame, hence the
three I phases:
• phase I0: between codons
• phase I1:: introns that start after 1st base
• phase I2 : introns that start after 2nd base
CG © Ron Shamir,
2008
9
Phylogenetic HMMs
• Due to Siepel and Haussler
• A simple gene-finding HMM looks at a
single Markov process:
• Along the sequence: each position is
dependent on the previous position
• If we incorporate sequences from multiple
organisms, we can look at another
process:
• Along the tree: each position is dependent on
its ancestor
Phylogenetic HMMs
• A simple HMM can be thought of as a
machine that generates a sequence
• Every state omits a single character
• Multinomial distribution at every state
• A phyloHMM generates an MSA
• Every state omits a single MSA column
• Phylogenetic model at every state
Phylogenetic HMMs
Phylogenetic models in
phyloHMM
• Defines a stochastic process of
substitution
• Every position is independent
• The following process occurs:
• A character is assigned to the root
• The character substitution occur based of some
substitution matrix and based on the branch
lengths
• The characters at the leaves of the tree
correspond to the MSA column
Phylogenetic models in
phyloHMM
• Different models for different states:
• Different substitution rates
• E.g., in exons, we’ll see less substitutions
• Different patterns of substitutions
• E.g., third position bias in coding sequences
• Different tree topologies
• E.g., following recombination
Formally
• S – set of states
• Ψ – phylogenetic models (instead of E in
a standard HMM)
• A – state transitions
• b – initial probabilities
Formally
• Q – substitution rate matrix (e.g., derived
from PAM)
• Π – background frequencies
• τ – the phylogenetic tree
• β – branch lengths
Formally
•
- Probability of a column Xi being
omitted by the model ψi
• Can be computed efficiently by
Felsenstein’s “pruning algorithm”
(recitation 6)
• Joint probability of a path in the HMM and
and alignment X
• Viterbi, forward-backward etc. – as usual
Simple phylo-gene-finder
Non-coding
3rd position
• If the parameters are known – Viterbi can be
used to find the most probably path –
segmentation into coding regions
Phylo-gene-finder is a good
idea
• Use of phylogeny is important:
• Imposes structure on the substitutions
• Weights different pairs differently based on
the evolutionary distance
N-SCAN
• Another phylogeny-HMM-gene-finder
• A GHHM that emits MSA columns
• Annotates one sequence at a time: the target
sequence
• Distinguishes between a target sequence – T
and other informative sequences (Is) that may
contain gaps
• States correspond to sequence types in the
target sequence
N-SCAN
• Bayesian network instead of a simple
evolutionary model
• Accounts for:
• 5’ UTRs
• Conserved non-coding
• Highly conserved
• No “coding” features
SGP-2
• Drawback of the described approaches:
require meaningful alignment
• Impossible if one of the genomes is not yet
finished
• An alignment is not necessary “correct”
SGP-2
• A framework working on two genomes
• Idea:
• Use BLAST to identify which positions are
more/less conserved
• Feed the BLAST scores into the gene-finding
HMM
• The BLAST results serve to modify the scores
of the exons.
SGP-2
BACH1
OLIG2
PPM1A
Summary
• Different approaches for gene finding
• Adding phylogeny generally helps
• But
• What about genes/exons which are specific to
humans
• Ape genomes are not (almost) available and too similar
• Phylogenetic help almost essential in more
difficult problems
• Motif finding (promoter analysis)
• Ultraconserved regions with no evident function