* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Models of Evolutionary Dynamics
Social Bonding and Nurture Kinship wikipedia , lookup
Sexual selection wikipedia , lookup
Gene expression programming wikipedia , lookup
Hologenome theory of evolution wikipedia , lookup
Natural selection wikipedia , lookup
E. coli long-term evolution experiment wikipedia , lookup
Coevolution wikipedia , lookup
Inclusive fitness in humans wikipedia , lookup
State switching wikipedia , lookup
Punctuated equilibrium wikipedia , lookup
Introduction to evolution wikipedia , lookup
Sociobiology wikipedia , lookup
Evolutionary psychology wikipedia , lookup
Genetics and the Origin of Species wikipedia , lookup
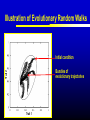
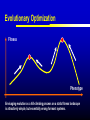
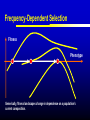
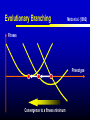
Models of Evolutionary Dynamics: An Integrative Perspective Ulf Dieckmann Evolution and Ecology Program International Institute for Applied Systems Analysis Laxenburg, Austria Mechanisms of Adaptation Imitation copy successful behavior Learning iteratively refine behavior Deduction derive optimal behavior Increasing cognitive demand Natural selection survival of the fittest Theories of Adaptation Population genetics Quantitative genetics Adaptive dynamics Evolutionary game theory 1930 1950 1990 1970 Overview Models of Adaptive Dynamics Connections with… Optimization Models Pairwise Invasibility Plots Quantitative Genetics Matrix Games Models of Adaptive Dynamics Four Models of Adaptive Dynamics PS MS MD PD These models describe… either polymorphic or monomorphic populations either stochastic or deterministic dynamics Individual-based Evolution Polymorphic and Stochastic Dieckmann (1994) Species N Species 1 ... Death Coevolutionary community Environment: density and frequency dependence Birth without mutation Birth with mutation Illustration of Individual-based Evolution Trait 2 Viability region Evolutionary trajectories Global evolutionary attractor Trait 1 Effect of Mutation Probability Small: 0.1% Mutation-selection equilibrium Mutation-limited evolution “Moving cloud” “Steps on a staircase” Evolutionary time Evolutionary time Trait Large: 10% Evolutionary Random Walks Monomorphic and Stochastic Mutation Dieckmann & Law (1996) Survival probability of rare mutant f+ / (f + d) Population dynamics Invasion Branching process theory Fixation Invasion implies fixation Death rate d Fitness advantage f Invasion probabilities based on the Moran process, on diffusion approximations, or on graph topologies are readily incorporated. Illustration of Evolutionary Random Walks Initial condition Trait 2 Bundles of evolutionary trajectories Trait 1 Illustration of Averaged Random Walks Trait 2 Mean evolutionary trajectories Trait 1 Gradient-Ascent on Fitness Landscapes Monomorphic and Deterministic Dieckmann & Law (1996) Canonical equation of adaptive dynamics d 1 * 2 xi i ( xi )ni ( x) i ( xi ) fi ( xi, x) x x i i dt 2 xi evolutionary rate in species i mutation probability equilibrium population size mutational variance-covariance local invasion selection fitness gradient Trait 2 Illustration of Deterministic Trajectories Evolutionary isoclines Evolutionary fixed point Trait 1 Reaction-Diffusion Dynamics Polymorphic and Deterministic Kimura (1965) Dieckmann (unpublished) Kimura limit 2 d 1 2 pi ( xi ) fi ( xi , p) pi ( xi ) i ( xi ) i ( xi ) 2 bi ( xi , p) pi ( xi ) dt 2 xi Finite-size corrections pi Additional per capita death rate results in compact support xi Summary of Derivations large population size small mutation probability small mutation variance PS MS MD large population size large mutation probability PD Optimization Models Evolutionary Optimization Fitness Phenotype Envisaging evolution as a hill-climbing process on a static fitness landscape is attractively simple, but essentially wrong for most systems. Frequency-Dependent Selection Fitness Phenotype Generically, fitness landscapes change in dependence on a population’s current composition. Evolutionary Branching Metz et al. (1992) Fitness Phenotype Convergence to a fitness minimum Phenotype Evolutionary Branching Branching point Directional selection Disruptive selection Time Pairwise Invasibility Plots Invasion Fitness Metz et al. (1992) Population size Definition Initial per capita growth rate of a small mutant population within a resident population at ecological equilibrium. + – Time Pairwise Invasibility Plots Mutant trait – + – Resident trait + + – Geritz et al. (1997) Invasion of the mutant into the resident population possible Invasion impossible One trait substitution Singular phenotype Reading PIPs: Comparison with Recursions Recursion relations Trait substitutions Next state Mutant trait – Current state Size of vertical steps deterministic + + – Resident trait Size of vertical steps stochastic Reading PIPs: Four Independent Properties Evolutionary Stability Convergence Stability Invasion Potential Mutual Invasibility Geritz et al. (1997) Reading PIPs: Eightfold Classification Pairwise Invasibility Plot Geritz et al. (1997) Classification Scheme Resident trait Evolutionary bifurcations Mutant trait (1) (2) (3) (4) (1) Evolutionary instability, (2) Convergence stability, (3) Invasion potential, (4) Mutual invasibility. Two Especially Interesting Types of PIP – + Branching Point + – Resident trait Evolutionarily stable, but not convergence stable Mutant trait Mutant trait Garden of Eden + – – + Resident trait Convergence stable, but not evolutionarily stable Quantitative Genetics An Alternative Limit large population size small mutation probability small mutation variance PS MS MD large population size large mutation probability PD given moments Infinite Moment Hierarchy 0th moments: Total population densities d dt ni n x σ 2 1st moments: Mean traits d dt xi n x σ 2 2nd moments: Trait variances and covariances d dt σ 2 i n x σ 2 skewness Quantitative Genetics: Lande’s Equation Lande (1976, 1979) & Iwasa et al. (1991) d 2 2 xi σi fi ( xi, x, n, σ ) xi xi dt xi rate of mean trait in species i local selection gradient fitness current population variance-covariance Population densities, variances, and covariances are all assumed to be fixed. Note that evolutionary rates here are not proportional to population densities. Game Theory: Strategy Dynamics Brown and Vincent (1987 et seq.) d dt ni ni fi ( xi , x, n, σ ) 2 d dt xi σ d dt σ 2 i xi fi ( xi, x, n,σ ) 2 xi xi 2 i Variance-covariance matrices may be assumed to vanish, be fixed, or undergo their own dynamics. Matrix Games Replicator Equation: Definition Assumption: The abundances ni of strategies i = A, B, … increase according to their average payoffs: d ni (Wn)i dt Their relative frequencies pi then follow the replicator equation: d pi (Wp )i p Wp dt Average payoff in entire population Replicator Equation: Limitations Since the replicator equation cannot include innovative mutations, it describes short-term, rather than long-term, evolution. The replicator equation for frequencies naturally arises as a transformation of arbitrary density dynamics. Owing to the focus on frequencies, the replicator equation cannot capture density-dependent selection. Interpreted as an equation for densities, the replicator equation assumes a very specific kind of density regulation. Other regulations will have altogether different evolutionary implications. Bilinear payoff functions based on matrix games imply additional limitations… Bilinear Payoff Functions Meszéna et al. (2001) Dieckmann & Metz (2006) Mixed strategies in matrix games have bilinear payoff functions, W ( p, p) p Wp , and an invasion fitness that is linear in the variant’s trait, f ( p, p) p Wp p Wp . For example, for the hawk-dove game, we have f ( p, p) 12 ( p p)(V pC ) . Meszéna et al. (2001) Dieckmann & Metz (2006) Degenerate PIPs The PIPs implied by a matrix game are thus highly degenerate: – + + – – + – + – + + – This degeneracy is the basis for the Bishop-Cannings theorem: All pure strategies, and all their mixtures, participating in an ESS mixed strategy have equal fitness. Example: Fluctuating Rewards Dieckmann & Metz (2006) If we assume rewards in the hawk-dove game to fluctuate between rounds (taking one of two similar values with equal probability), the PIP’s degeneracy immediately vanishes: – + + – Accordingly, the structurally unstable neutrality of invasions at the ESS is overcome. This resolves the ambiguity between population-level and individual-level mixed strategies. Two-Dimensional Unfolding Dieckmann & Metz (2006) of Degeneracy Game-theoretical case straddles two bifurcation curves and thus acts as the organizing centre of a rich bifurcation structure. Mixtures of Mixed Strategies Dieckmann & Metz (2006) Evolutionary outcomes can now be more subtle: + + One mixed strategy + + Two pure strategies + + A pure and a mixed strategy + + Two mixed strategies The interplay between population-level polymorphisms and individual-level probabilistic strategy mixing thus becomes amenable to evolutionary analysis. Summary Models of adaptive dynamics offer a flexible toolbox for studying phenotypic evolution: Simplified models are systematically deduced from a common individualbased underpinning, providing an integrative perspective. The resultant models are particularly helpful for investigating the evolutionary implications of complex ecological settings: Frequency-dependent selection is essential for understanding the evolutionary formation and loss of biological diversity.