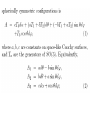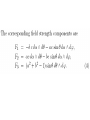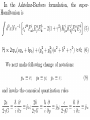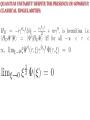* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Two-body Dirac equations wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Higgs mechanism wikipedia , lookup
EPR paradox wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Wave–particle duality wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Renormalization wikipedia , lookup
Quantum state wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum field theory wikipedia , lookup
Gauge fixing wikipedia , lookup
Path integral formulation wikipedia , lookup
Dirac equation wikipedia , lookup
Renormalization group wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
BRST quantization wikipedia , lookup
Hidden variable theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
AdS/CFT correspondence wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Scalar field theory wikipedia , lookup
Dirac bracket wikipedia , lookup
History of quantum field theory wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Is Black Hole an elementary particle?
By
Hoi-Lai Yu
IPAS, Oct 30, 2007
Basic Questions in searching the Truths of Nature:
What is Space?
What is Time?
What is the meaning of being somewhere?
What is meaning of “moving”?
Is motion to be defined with respect to objects or with respect to space?
Can we formulate Physics without referring to time or space?
What is matter?
What is causality?
What is the role of Observer in Physics?
Active Diffeormophism invariant
What disappears in GR is precisely the
background space time that Newton believed
to have been able to detect.
Reality is not made by particles and fields on
Spacetime.
Reality is made by particles and fields
(incldue gravity), that can only be localized with
respect to each other.
Puzzles in general relativity
(1)Black holes entropy
A
S
4G
(2)Cosmology: Big Bang
Singularity
Results on Loop Quantum Gravity
• Non Perturbative Gravity
• Canonical Analysis in ADM variables
• Using the new variables: triad formailism,
Ashtekar-Barbero variables
• Geometric interpretation of the new variables
• Quantization of triad, area, volume,…
• Results: Non commutativty of the geometry,
inflation, Black hole thermodynamics, ringing
modes frequencies, Bekenstein-Mukhanov
effect
Canonical Analysis in ADM variables
Geometric theories of gravity and fields:
Foliation of spacetime ( x R) into: space-like 3 dim
surfaces
Time has 2 aspects:
(1)Instant of time → t=constant spacelike surfaces
(2) Time evolutions
→ a “timelike” vector field
Gravity as a gauge theory:
How can one works only with a gauge field without
metric?
In Hamiltonian language point of view:
space-time manifold of the form x R describing by:
Astekhar connection, Aai
and its conjugate momentum, Eai
where a is a 3d spatial index and i is valued in a lie
algebra, G
We have Poisson brackets:
{ Aai (x) , Ebj (y) } = ab ij 3 (y,x)
In a hamiltonian formulation of a gauge
theory :
one constraint for each independent
gauge transform. The gauge invariance of a
gravitational theory include at least
4 diffeomorphisms, per point.
(1) Ha generates the diffeomorphisms of ,
(2) H is the Hamiltonian constraint that generates the rest of the
diffeomorphism group of the spacetime (and hence changes of the
slicing of the spacetime into spatial slices),
(3) Gi generates the local gauge Transformations,
(4) h terms in the Hamiltonian that are not proportional to
constraints. However, there is a special feature of gravitational
theories, which is there is no way locally to distinguish the changes in
the local fields under evolution from their changes under a
diffeomorphism that changes the time coordinate. Hence h is always
just a boundary term, in a theory of gravity.
(1) From Yang-Mills theory the constraint that generates local gauge
transformations under the Poisson bracket is just Gauss's law:
Gi = Da Eai = 0
(2) Three constraints per point that generate the differomorphisms
of the spatial slice.
Infinitesimally these will look like coordinate transformations, hence
the parameter that gives the infinitesimal change is a vector field.
Hence these constraints must multiply a vector field, without using a
metric.
Thus these constraints are the components of a one form. It should
also be invariant under ordinary gauge transformations, as they
commute with differomorphisms. We can then ask what is the
simplest such beast we can make using Aia and Eai ?
The answer is
Ha = Ebi Fiab = 0
where Fiab is the Yang-Mills field strength.
(3) One constraint per point, which generates changes in
the time coordinate, in the embedding of M = x R.
This is the Hamiltonian constraint.
Since its action is locally indistinguishable from the effect
of changing the time coordinate, it does contain the
dynamics since the parameter it multiplies is proportional
to the local change in the time coordinate. It must be
gauge invariant and a scalar. But it could also be a density,
so we have the freedom to find the simplest expression that
is a density of some weight. It turns out there are no
polynomials in our fields that have density weight zero,
without using a metric. But two expressions have density
weight two. The two simplest such terms that can be
written, which are lowest order in derivatives,
In fact these two terms already give Einstein's equations,
so long as we take the simplest nontrivial choice for G,
which is SO(3). Thus, we take for the Hamiltonian
constraint:
being the cosmological constant.
Aa is a connection and so has dimensions of inverse length.
It will turn out that Ea is related to the metric and so we
should make the unconventional choice that it is
dimensionsless.
In fact, what we have here is Euclidean general relativity.
If we want the Lorentzian
theory, we need only modify what we have by putting an “i”
into the commutation relations
SEMICLASSICAL LIMIT, HAMILTON-JACOBI EQUATIONS,
AND SCHWARZSCHILD BLACK HOLES
We may furthermore map precisely the equation of motion for plane
wave solutions to classical black holes by studying the
correspondence of the classical initial data to the Hamilton-Jacobi
theory. To achieve this, we note that the familiar Schwarzschild
metric is:
So, now we have seen that a black hole is really a
elementary partice in superspace with definite
dispersion relation:
K+ K - = 1
RINDLER SUPERSPACE
The Minkowski Bessel modes can in fact be understood as the “rapidity
Fourier transform" of plane wave solutions
The Dirac equation which is first-order in superspace intrinsic time on
the Rindler wedge,
QUANTUM UNITARITY DESPITE THE PRESENCE OF APPARENT
CLASSICAL SINGULARITIES
An analogous situation happens in free non-relativistic
quantum mechanics wherein hermiticity of the momentum
operator requires a physical Hilbert space of suitable
wavepackets which vanish at spatial infinity, and rule out
plane wave states with infinitely sharp momentum. From this
perspective the boundary condition guaranteeing quantum
unitarity in our present context of spherically symmetric
gravity holds for rather generic wavepackets.
Replacing the “Quantum censorship” by BC
with nonzero wave-function at
the classical singular, zero-volume three
geometry (but allowing the topological
fluctuations) which may correspond
to Big Bang singularity may give non-trivial
example interpretation of
Hawking-Hartle boundary without boundary
condition of creating the Universe
from nothing!
Summary:
(1) The resultant arena for quantum geodyanmics is two dimernsion of signature
(+,-), non-singular – intrinsic time and R radial coordinate time
are monotonic function of each other.
(2) Black holes are elementary particles in superspce.
(3) The boundary of the Rindler wedge corresponds to physical horizons and
singularities of Black Holes.
(4) Hamilton_Jacboi semi-classical limits consists of plane wave solution can be
matched previously to interiors of Schwarzchild black holes with straight line
trajectories of free motion in flat superspace – quantum Birkhoff theorem.
(5) Sperspace is free of singularity even in continuum.
(6) Positive definite current can be obtained for wave-functions on superspace
for Dirac equation associated with WdW equation.
(7) Hermiticity of Dirac Hamiltonian and thus Unitary of quantum theory is
translated BC on the space like hypersurfaces of Rindler Wedge which is
better for Hartle-Hawking mechanism for creation of Universe.