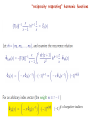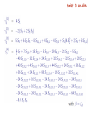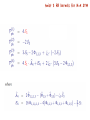Download Classical tunes of Gluon Dynamics

Classical tunes
of Gluon Dynamics
(II)
Yuri Dokshitzer
LPTHE Jussieu, Paris
& PNPI, St Petersburg
Paul Hoyer - Fest
November 2013
Parton Evolution
and
Higher Loops
Higher orders’ headache
Recent years were/are marked by explosive progress in analytic
calculations of multi-leg QFT amplitudes and multi-loop corrections
It took 3-4 years (1976 -> 1980) to establish the next-to-leading
(2-loop) parton Hamiltonian (splitting functions).
It took another 20+ years to calculate the DIS anomalous
dimensions in three loops.
This is no doubt an enormous achievement
which leaves, however, that air of deep sadness ...
Have a look at the simplest element of the an.dim. matrix
corresponding to the non-singlet (valence quark) evolution
To remind you : the simplest “matrix element”
of the parton “Hamiltonian” in the 1st loop
1+x
Pqq (x) = CF
1−x
2
well . . .
not too encouraging a trend . . .
quest
How to reduce complexity ?
An essential part of gluon dynamics is
However, it has a good chance to be
Classical.
Exactly Solvable.
Innovative
Bookkeeping
Yesterday we recalled the basics
of the QCD parton picture
and introduced the notion of the
parton fluctuation time
L L A
Which are the most probable parton fluctuations?
(
)n
(
)n
Such contributions should - and can - be resummed in all orders !
Kinematics of the parton splitting A
B+C
kB = zkA , kC = (1 − z)kA
Relation between virtualities of three participating partons :
Probability of the splitting process
To gain a large logarithmic enhancement, we have to have
This inequality has a transparent physical meaning :
strongly ordered
lifetimes
of successive parton fluctuations
Evolution of a parton system becomes a Markov chain in a properly chosen “time”, ~ ln Q2
This was about partons in the space-like region
“pdfs”
The same picture of parton cascades
applies to multiplication
of partons in jets
“fragmentation functions”
=
the time-like evolution
space- vs. timeDrell-Levy-Yan relation :
Gribov-Lipatov reciprocity relation (GLR) :
PBA (x) = ∓ x PAB (x
−1
Breaks down
)
beyond the 1st loop
...
BUT can be resurrected in all orders !
Curiously it might seem, but nobody uses
the evolution time variable we have derived
- fluctuation time to treat parton multiplication...
It there a reason for that?
Yes. And a good one
Quantum Coherence
Analyzing Feynman denominators, we came to “fluctuation time ordering”
t[q]
βk
βq
! 2 ! 2 ! t[k]
q⊥
k⊥
β ∼ Q2 /s
q
k
β∼1
If we used this in earnest, the evolution equations would have become
non-local since the dependence of pdfs on Q and the dependence on x would mix ...
In fact, no-one does so. Why ?
In the LLA (1-loop level), the beta-factors can be dropped altogether.
However, nowadays the DIS phenomenology employs the three-loop parton dynamics !
Already beyond the 1st loop (LLA), it starts to matter how to order successive parton
splittings that is, which variable to choose for "parton evolution time".
This choice affects higher-loop “anomalous dimensions” - our “Hamiltonian”.
The "clever choices" had been established quite some time ago:
( Gribov & Lipatov )
Transverse momentum ordering
space-like parton evolution; DIS structure functions
2
k⊥
dξ = d ln
1
2
k⊥
dξ = d ln 2
z
Each is a consequence of taking into full consideration soft gluon coherence to prevent
explosively large terms (αs ln2 x)n from appearing in higher loop anomalous dimensions.
Angular ordering
( Fadin & Mueller)
time-like parton multiplication; jet fragmentation functions
Space-like parton evolution: DIS at small Bjorken x
q
t[q]
βk
βq
! 2 ! 2 ! t[k]
q⊥
k⊥
BFKL
k⊥ integration phase space
swells when βq / βk → 0
(high energy hard scattering)
αs
!
dβ
β
βq ! βk
k
αs ln s
NO αs ln2 s terms... How has this happened? Quantum-mechanical coherence at work !
q
0
k
:
In a long-range potential :
Inelastic dissociation. Into a compact state
−1
∆ρ⊥ ∼ k⊥
−1
λ⊥ ∼ q⊥ "
∆ρ⊥
In QCD/QED vanishing of forward inelastic processes follows from gauge invariance.
In a more general context, it is due to orthogonality of the initial and final state wave
functions, provided the initial and final systems interact identically with “the probe”.
evolution time
We see that the “kinematical” fluctuation time ordering
seems to be of little relevance as it misses essential physics.
t[q]
βk
βq
! 2 ! 2 ! t[k]
q⊥
k⊥
Thus, in order to take into consideration destructive interference effects we have to replace
ordered lifetimes
by ordered transverse momenta
Formally, such a step is unnecessary (though convenient) to take in the Leading Log Approximation
where we keep track, exclusively, of the leading transverse momentum logarithms.
In higher orders, in becomes mandatory as it avoids appearance of superficial double
logarithms in the anomalous dimension of DIS at x ! 1 .
Production of relatively soft gluons in time-like cascades (jets)
Formation time of the gluon :
ϑ0
tform
1
k
! 2 = λ⊥ ·
k⊥
Θ
Let us look at the distance between the radiating color charges.
During this time they separate in the transverse plane by
∆ρ⊥ ! tc · ϑ0
Now compare this separation with the wavelength of the radiation :
ϑ0
∆ρ⊥
=
λ⊥
Θ
If this ratio is larger than 1, Θ < ϑ0 , the gluon will be radiated independently
by the two partons of the previous generation.
Otherwise, gluon radiation intensity will be determined by the overall color charge
of the parton pair. Soft gluon coherence!
Probabilistic parton cascades
Angular Ordering
intra-jet coherence
Destructive interference suppresses multiple production of very small momentum gluons.
It is particles with intermediate energies that happen to multiply most efficiently !
The energy spectrum of relatively soft secondary partons in jets develops a “hump ”.
The position, the width and the height of this hump evolve with Q2 in a predictable way.
This prediction was derived in 1984 in the so-called MLLA (Modified Leading Log Approximation).
It took into account essential ingredients of parton multiplication in the next-to-leading order :
parton splitting functions responsible for the energy balance in parton splitting
the running coupling depending on the relative transverse momentum of the offspring
the exact angular ordering. The latter - a consequence of soft gluon coherence.
Moreover, in turned out that “soft jet fragmentation” can be predicted, in certain sense,
from the first principles unlike DIS parton distributions where one always needs a NP input.
The shape of the inclusive spectrum of all charged hadrons (dominated by pions)
exhibits the same features as the MLLA parton spectrum
First scrutinized at LEP, the similarity of parton and hadron energy spectra has been verified at
SLC and KEK e+e- machines, as well as at HERA and Tevatron (where jets originate not from
quarks dug up from the vacuum by a virtual photon/Z0 but from partons kicked out from initial hadron(s)).
LPHD IN-JETS
The comparison of the spectra of all charged
hadrons at various annihilation energies Q
with the so-called “distorted Gaussian” fit
which employs the first four moments
( the mean, width, skewness and kurtosis )
of the MLLA distribution around its maximum.
Shall we say : a
(routine, interesting, wonderful)
check of yet another QCD prediction?
Such a close similarity offers a deep puzzle,
even a worry, rather than a successful test
1 GeV
420 MeV
850 MeV
Тhe observation of the parton-hadron similarity was initially met with a serious
scepticism: it looked more natural to blame the finite hadron mass effects for
falloff of the spectrum at large ξ (small momenta) rather than seriously believe
in applicability of the PT consideration down to such disturbingly small scales.
However, it is not the energy of the jet but the maximal parton transverse momentum inside it,
k⊥max ! Ejet sin Θcone that determines the hardness scale of the process,
and thus the yield and the distribution of the accompanying radiation.
This means that by choosing a small opening angle one can study relatively small hardness scales
but in a cleaner environment : due to the Lorentz boost effect, eventually all particles that form
a short small-Q2 QCD “hump” are now relativistic and are concentrated at the tip of the jet !
Selecting hadrons inside a cone 0.14 around a
quark jet with Ejet=100 GeV one would see that
very dubious Q=14 GeV curve but now with the
maximum boosted from 0.45 GeV to 6 GeV !
jets with restricted “opening angle”
as a function
of the hardness of the jet
is a parameter-free pQCD prediction
The plot combines e+e-, DIS and hh data !
CDF
punchline
The ratios of particle flows between jets (intERjet radiophysics),
as well as the shape of the inclusive spectra of secondary particles (intRAjet cascades)
turn out to be formally calculable (CIS) quantities.
Moreover, the perturbative QCD predictions actually describe flows of hadrons !
The strange thing is, these phenomena reveal themselves in present-day experiments via
hadrons (pions) with extremely small momenta k⊥ , where we are expecting to hit the
non-perturbative domain — large coupling αs (k⊥ ) — and potential failure of the
quark–gluon language as such.
The fact that the underlying perturbative dynamics of color is being impressed upon
“miserable” pions with 100–300 MeV momenta, could not be a priori expected.
At the same time, it repeatedly sends us a powerful message: confinement –
transformation of quarks and gluons into hadrons – has a non-violent nature:
there is no visible reshuffling of energy–momentum at the hadronization stage.
Known under the name of the Local Parton-Hadron Duality hypothesis (LPHD),
explaining this phenomenon remains a challenge for the future quantitative
theory of color confinement.
Heat is building up, and QCD is undergoing
a faith transition
We spoke about “clever” (physical) choices of the parton evolution time(s)
The "clever choices" had been established quite some time ago:
( Gribov & Lipatov )
Transverse momentum ordering
space-like parton evolution; DIS structure functions
2
k⊥
dξ = d ln
1
Angular ordering
( Fadin & Mueller)
time-like parton multiplication; jet fragmentation functions
2
k⊥
dξ = d ln 2
z
From this (.) of view, the fluctuation time ordering ainʼt a clever one
Fluctuation time ordering
dξ = d ln
2
k⊥
z
It is “not physical”, either in the DIS or e+e- environment.
Interestingly, it is not simply wrong. It is wrong in a symmetric manner !
No wonder,
the GL reciprocity gets resurrected in all orders
by returning to the
fluctuation time
as evolution variable
!
Such an “unphysical” modification of the parton
evolution equations makes the “evolution kernels”
universal, DIS = e+e-,
and tremendously simplifies the path to higher
order anomalous dimensions by realizing the idea
of “inherited complexity”
Now we turn to the second part of our quest
- the “Think-Extract-Solve” attempt to make
QCD simple(r)
recall
Low-Barnett-Kroll wisdom
and the story of
“classical gluons”
GLR & LBK
Apparent and Hidden symmetries of parton dynamics
Hamiltonian
QED
+
=
Color factors were excluded from the game ...
+ infinite number of hidden invariants ! ..
+
Super-Symmetric partner of QCD
CF=TR=CA (=NC)
Clagons and Integrability
Is a given infinity infinite enough as to make the theory solvable ?
In certain specific problems where one can identify QCD with its SUSY partner theory
the integrability feature manifests itself !
N=4 SYM
The higher the symmetry, the deeper integrability ...
N=4 SYM — the extreme case !
What is so special about this theory ?
look at the anomalous dimension :
(parton evolution “Hamiltonian”)
=0
N=4 SYM
Maximally super-symmetric N=4 YM allowed for a compact
analytic solution of the GLR problem in 3 loops (all moments N)
D-r & Marchesini (2006)
4 loops
Beccaria & Fiorini (2009)
5 loops
Romuald Janik & Co (2010+)
... ALL loops ?
Let us examine what sort of functions
the N=4 parton Hamiltonian is made of
Euler’s Harmonic Sum
Euler-Zagier harmonic sums
twist 2 an.dim. for N=4 SYM
“reciprocity respecting” harmonic functions
(−1)# of negative indices
twist 2 RR kernels for N=4 SYM
twist 3 an.dim.
twist 3 RR kernels for N=4 SYM
why care ?
N =4 SYM dynamics is classical, in (un)certain sense
No truly quantum effects are being seen
punchline
A steady progress in high order perturbative QCD calculations is worth accompanying
by reflections upon the origin and the structure of higher loop correction effects
Reformulation of parton cascades in terms of the Gribov–Lipatov reciprocity
respecting evolution equations (RREE)
reduced complexity by (at least) an order of magnitude
improved perturbative series (less singular, better “converging”)
linked interesting phenomena in the DIS and e+e− annihilation channels
The Low theorem should be part of theor. phys. curriculum, worldwide
A complete solution of the N=4 SYM QFT should provide us one day
with a one-line-all-order description of the major part of QCD parton dynamics
Understanding of the anomalous production of “soft photons” in lepton-hadron
and hadron-hadron interactions should generate an important information
about the nature of color confinement ...
a missing piece
instead of conclusions
Physics of hadrons and their interactions has never been simple, and will never be.
Certain simplifications occur at large momentum transfer (asymptotic freedom)
as well as at large interaction energies (TCAM, the “old theory”)
To progress, one needs to master and exploit both.
make sure that your library possesses the Book
Strong Interactions of Hadrons at High Energies
Gribov lectures on theoretical physics
CUP 2008