* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Review: Castro-Neto et al, Rev. Mod Phys. Abanin, Lee and Levitov
Renormalization wikipedia , lookup
Wave function wikipedia , lookup
Quantum entanglement wikipedia , lookup
Renormalization group wikipedia , lookup
Magnetic monopole wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
EPR paradox wikipedia , lookup
Dirac equation wikipedia , lookup
Canonical quantization wikipedia , lookup
Quantum state wikipedia , lookup
Hydrogen atom wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Scalar field theory wikipedia , lookup
Ising model wikipedia , lookup
Two-dimensional nuclear magnetic resonance spectroscopy wikipedia , lookup
Electron paramagnetic resonance wikipedia , lookup
History of quantum field theory wikipedia , lookup
Nitrogen-vacancy center wikipedia , lookup
Bell's theorem wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Ferromagnetism wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Spin (physics) wikipedia , lookup
Review:
Castro-Neto et al, Rev. Mod Phys.
Abanin, Lee and Levitov, Solid state communications, 143 77 (2007),
part of special volume on graphene.
Outline:
Review the origin of Dirac spectrum.
Special properties of Dirac spectrum: transport, localization and screening.
Quantum Hall effect in graphene vs conventional 2DEG.
Quantized spin Hall current and spintronics.
Nature of the ν=1 Landau level: order by disorder.
Review of the topological insulator.
0Å
9Å 13Å
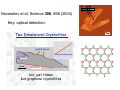
Novoselov et al, Science 306, 666 (2004)
Key: optical detection.
Two Dimensional Crystallites
crystal faces
zigzag
10 μm
armchair
not just flakes
but graphene crystallites
1 µm
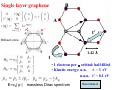
Single layer graphene
B
A
t’
Brillouin zone
1.42 A
t
• 1 electron per π orbital: half-filled
• Kinetic energy: n.n. t ~ 3 eV
n.n.n. t’ ~ 0.1 eV
E=v0| p |
massless Dirac spectrum
See notes A
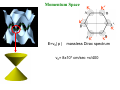
Momentum Space
E=v0| p |
massless Dirac spectrum
v0= 8x107 cm/sec =c/400
Klein paradox:
Transmission thru arbitrarily high barrier.
Transmission probability T=1 for
forward direction ,(ie reflection
R=0 ), due to conservation of
pseudo-spin.
Katsnelson,Novoselov and
Geim,Nature Phys. 2, 620 (2006)
Absence of localization for any disorder strength for a single Dirac node!
1. No bound state for arbitrarily deep potential: always scattering state
because there is no band bottom.
2. Naively expectation is “symplectic class” which has anti-localization.
Recent work by Nomura, Koshino and Ryu (PRL 99, 146806 (2007))
showed that unlike the symplectic case, there is no transition to insulator.
3. If inter-node scattering is small (smooth potential), we may expect
positive magneto-resistance. Experimentally, almost no magnetoresistance is observed. Explanation was proposed in terms of buckling of
graphene layers. (Morozov et al, PRL 97, 016801 (2006).) More later.
Electric Field Effect in Graphene
conductivity σ=n(Vg)eμ
Hall effect
electrons
B =2T
T =10K
10
2
0
holes
1
T =10K
0
-100
-50
0
50
100
Vg (V)
SiO2
Si
Au
contac
ts
GRAPHENE
1/ρxy=ne/B
-100
1/ρxy (1/kΩ)
σ (1/kΩ)
3
-10
-50
0
50
100
Vg (V)
simple behaviour;
practically constant mobility;
no trapped carriers
Electric conductivity single layer
Universal DC conductivity
h
Simple argument:
σ ~ N(0)D.
N(0) ~ 1/τ. D~v^2*τ/2
ρmax (h/4e2)
2
15 devices
1
0
μ (cm2/Vs)
0
4,000
8,000
Mystery of the missing
π
Puddles of n and p type domains?
(Altshuler et al)
Interaction effect:
Incomplete screening at the Dirac point.
Dimensionless coupling constant is
(unlike e^2/c for QED)
Constant mobility due to partial screening of charged
impurity (McDonald) , or buckling of layers.
Pertubation theory
P
h
y
s
.
R
e
v
.
B
.
{
\
b
f
7
2
}
,
1
7
4
4
0
6
(
2
0
0
5
)
Not like a Fermi Liquid!
Gonzalez et al. PRL 77, 3589 (96)
Strong coupling treatment by 1/N expansion, D. Son PRB75, 235423 (2007).
Predicts a power law dispersion E(k) ~ k^(1-α), α~1/N.
In the presence of a magnetic field B: Landau levels
ωc = eB /(mc) = h /(mlB2 )
l B = hc /(eB)
B = 10T
hωc ≈ 1K
B=10T, E1-E0=1500K
Zero mode
QHE at room temperature!
Existence of a zero eigenstate is a general feature.
For example, for arbitrary B(r) , Aharonov and Casher (PRA 19 2461 (1979)
showed that E=0 is a normalizable eigenstate. (this is a special case of what
is called index theorem.
graphene
3
5/
2
3/
2
2
1
1/
2
0
-1/2
-1
-3/2
-5/2
σxy (4e2/h)
σxy (4e2/h)
7/
2
-2
-3
-7/2
-4
ρxx (kΩ)
6
T =4K
4
B =12T
2
0
Y.Zhang et al., Nature 438, 201 (05)
-4
-2
0
2
4
n (1012 cm-2)
Novoselov et al., Nature 438, 197 (05)
29T
4
2
20
10
0
room
temperature
-2
σxy (e2/h)
ρxx (kΩ)
30
-4
0
-60
-6
-30
0
30
60
Vg (V)
Novoselov et al, Science 315, 1379 (2007)
IR absorption:
Jiang,…P. Kim and H. Stormer, PRL 98,197403 (2007)
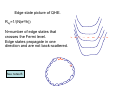
Edge state picture of QHE.
Rxy=1/(N(e2/h))
N=number of edge states that
crosses the Fermi level.
Edge states propagate in one
direction and are not back-scattered.
See notes B
graphene
3
5/
2
3/
2
2
1
1/
2
0
-1/2
-1
-3/2
-5/2
-2
-3
-7/2
-4
ρxx (kΩ)
6
Spin
splitting
T =4K
4
B =12T
2
0
-4
-2
0
2
n (1012 cm-2)
4
σxy (4e2/h)
σxy (4e2/h)
7/
2
LLandauer-Buttiker Picture of transport: transmitting and reflecting channels.
Application to QHE: Ballistic chiral channels.
Contacts:
Current leads: Charge reservoir with local
chemical potential V.
Ιnject current I with energy less than V.
I=(e^2/h)V per channel.
Absorb all incoming electrons.
Voltage leads.
Iin=Iout
equilibrium voltage V,
same for both spins.
Spin filtered edge states.
Abanin, Lee and Levitov, PRL96,176803(2006)
Spin up moves left
Spin down moves right
Simple example of a
topological Hall insulator.
(Kane and Mele,PRL2005)
where gap is opened by
spin-orbit effect.
No Hall voltage Rxy=0 , but ideal spin current: Is=2e2V/h.
Polarized spin current generator:
Simply remove one voltage probe.
4 probe longitudinal resistivity measurement:
Backscattering require spin flip. Spin
flip scattering will reduce Gxx from 2.
Spin orbit coupling is estimated to be
very weak.
1.Rashba term 0.5mK
2 Intrinsic term λσz require
parallel magnetic field.
Mostly likely there are some magnetic
impurities.
Indeed spin flip rate is so slow that
nonlocal spin valve effect has been
observed even at room temperature.
(Tombros …van Wees, Nature 448,
571 (2007))
Jiang et al PRL99 106802 (2007)
Abanin et al , PRL98,196806(2007)
We also predict non-local transport. Voltage leads far away can affect current.
Generation and detection of spin current:
Nonlocal transport.
Our entire picture assumes spin splitting is
greater than orbital splitting (between K and K’).
Otherwise, we have a regular insulator. We
estimate the energy difference of K ,K’ for n=0
level to be very small. Nonlocal transport is a
key expt test.
This raises the question which orbital state is
preferred.
Tilted field experiment supports our level splitting scheme:
Jiang et al PRL99,106802(2007)
Distortion of the bonds due to
strain or buckling is equivalent to a
random gauge field a, which
couples to K,K’ nodes with
opposite signs. (Iordanskii and
Koshelev, 1985)
height ≈5Å; size ≈5nm;
Consequences of random gauge fields:
1. Equivalent field is quite large (0.1T to 1T).
2. Explains why weak localization is not seen (or suppressed in some
samples).(Morozov et al PRL 06)
3. Order out of disorder: select a linear combination of K, K’ to be the
occupied ν=-1 state. (Abanin, Lee and Levitov, cond-mat,06)
Pseudo-spin picture: K is spin up and K’ spin down.
(like the bilayer quantum Hall problem).
Prediect XY transition and meeron (1/2 integer excitation)
Perhaps not the whole story!
Checkelsky, Li and Ong, cond-mat.
Topological insulator.
Question: can we have quantum Hall like behavior without an external magnetic
field? ,ie can we have energy gap in the bulk (insulator) and gapless edge states
without breaking T reversal symmetry?
Such edge state will lead to quantum spin Hall effect. (which, unlike ordinary QHE,
does not break T, as emphasized by SC Zhang.)
1. Haldane (1988) showed that spatially varying B with net flux zero can
cause QHE.
2. Kane and Mele (2005) showed that graphene with spin-orbit coupling gives
rise to spin-filtered edge states without breaking of time reversal symmetry.
Z2 topological classification proposed.
3. SC Zhang and collaborators (2006) proposed experimental realization in
Hg-Te quantum well.
4. Expt performed and predictions verified by Konig et al (2007).
How to give a energy gap (mass in particle physics language) to graphene?
1. NNN hopping t’ give uniform shift of enegy
band. (breaks particle-hole symmetry), but
does not open gap.
2. One way is to have different potential energy at
A and B sites. Breaks parity but preserves time
reversal T. Sign of mass the same for K and K’.
3. Second way is to have complex t’ as
suggested by Haldane. Sign of mass is
opposite for K and K’ and T is broken.
Haldane showed that in case 3, QHE=1
or -1, depending on the sign of m when
fermi energy is in the gap.
Kane and Mele (PRL 95, 226801(2005)) added spin degrees of freedom
to restore time reversal symmetry in the Haldane model. This is produced
by the spin-orbit coupling term in graphene.
Edge states are time reversed pairs, exactly
like the zeroth landau level case we studied,
except that there is no magnetic field and the
gapless edge modes are protected by time
reversal symmetry. Unfortunately spin-orbit
gap is very small (10mK)
Bernevig, Hughes and Zhang, Science 314,1757(2006)
In a quantum well, gap is opened ,4 band model..
Konig et al, Science 318, 766(2007)
3 Dimensional example is also possible:
Edge states will be 2Dim Dirac spectrum.
These are predicted to show anomalous Hall effect. (Foo and
Kane, PRB76,045302 (2007))
Possible examples are grey tin and HgTe
under uni-axial stress to open a gap.
Also Bi Sb alloys.
Other 2D Atomic Crystals
2D boron nitride in AFM
0Å
9Å
16Å 23Å
2D NbSe2 in AFM
0Å
8Å
23Å
1μm
0.5μm
1 μm
2D Bi2Sr2CaCu2Ox in SEM
1μm
1 μm
2D MoS2 in optics
Geim et al PNAS
102,
10451 (2005)
Special features of graphene:
Strong bonding, robust layer structure: Large layer
with high mobility.
Dirac spectrum: large gating effect and new physics.
Weak spin-orbit coupling and spin flip scattering.
Here we discussed interesting spin current effects.
Other applications:
Graphene based electronics and spintronics?
superconducting FET. (Delft group, Heersche et al,
Nature 446,56(2007)).
Resonator,
Molecule sensor …….
Bunch et al
Science (07)
Schedin et al. Nature Mat. (07)