Download Lehninger Principles of Biochemistry

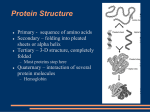
Chap. 6A Enzymes
• Introduction to Enzymes
• How Enzymes Work
• Enzyme Kinetics as an Approach to
Understanding Mechanism
• Examples of Enzymatic Reactions
• Regulatory Enzymes
Fig. 6-22. The chymotrypsin
enzyme-substrate complex.
Intro. to Enzymes
All living organisms must be able to self-replicate and catalyze
chemical reactions efficiently and selectively. Enzymes (from the
Greek enzymos, “leavened”) are the chemical catalysts of
biological systems. Enzymes have extraordinary catalytic power,
often far greater than that of synthetic or inorganic catalysts.
They have a high degree of specificity for their substrates and
they accelerate chemical reactions tremendously. They function in
aqueous solutions under very mild conditions of temperature and
pH, unlike many catalysts used in organic chemistry. Enzymes are
central to every biochemical process. They catalyze the hundreds
of stepwise reactions of metabolism, conserve and transform
chemical energy, and make biological macromolecules from simple
precursors. In many diseases, the activity of one or more
enzymes is abnormal. Many drugs act via binding to enzymes.
Chemical Features of Enzymes (I)
With the exception of a small group of catalytically active RNA
molecules (Chap. 26), all enzymes are proteins. Their catalytic
activity depends on the integrity of their native protein
conformation. Some enzymes require no chemical groups for
activity other than their amino acid residues. Others require an
additional chemical component called a cofactor. Cofactors can be
inorganic ions (Table 6-1), or complex organic or metalloorganic
molecules called coenzymes (Table 6-2, next slide).
Chemical Features of Enzymes (II)
Coenzymes usually act as transient carriers of specific functional
groups (Table 6-2). Most are derived from vitamins, which are
organic nutrients that are required in small amounts in the diet.
Some enzymes require both a coenzyme and one or more metal ions
for activity. A coenzyme or metal ion that is very tightly or even
covalently bound to an enzyme protein is called a prosthetic group.
A complete, catalytically active enzyme together with its bound
coenzyme and/or metal ion is called a holoenzyme. The protein part
of such an enzyme is called the apoenzyme or apoprotein. Many
enzymes are modified by phosphorylation or other processes.
Modifications often are used to regulate enzyme activity.
Enzyme Classification
Many enzymes have been named by adding the suffix “-ase” to the
name of their substrate or to a word or phrase describing their
activity. Biochemists by international agreement have adopted a
system for naming and classifying enzymes based on the type of
reaction catalyzed (Table 6-3). Each enzyme is assigned a fourpart classification number and a systematic name, which identifies
the reaction it catalyzes. For example the enzyme know commonly
as hexokinase is formally ATP:glucose phosphotransferase. Its
Enzyme Commission number is 2.7.1.1, in which the first number
(2) denotes the class name (transferase); the second number (7),
denotes the subclass (phosphotransferase); the third number (1), a
phosphotransferase with a hydroxyl group as acceptor; and the
fourth number (1), D-glucose as the phosphoryl group acceptor.
Enzyme Active Sites
Under biologically relevant conditions,
uncatalyzed reactions tend to be slow
because most biological molecules are
quite stable in the neutral-pH, mildtemperature, aqueous environment inside
cells. Enzymes greatly increase the rates
of biological reactions by providing a
specific environment within which a
reaction can occur more rapidly. Enzymecatalyzed reactions take place within the
confines of a pocket on the enzyme called
the active site. The reactant molecule is
referred to as the substrate. The
surface of the active site is lined with
amino acid residues with substituent
groups that bind to the substrate and
catalyze its chemical transformation.
Often, the active site encloses the
substrate, sequestering it from solution.
The active site of the enzyme
chymotrypsin is highlighted in Fig. 6-1.
Enzymes Affect Rxn Rates, Not Equilibria (I)
Any reaction, such as S  P, can be described by a reaction
coordinate diagram, in which the free energy change during the
reaction is plotted as a function of the progress of the reaction
(Fig. 6-2). The free energy change (∆G’0) (and equilibrium position)
of the reaction is determined by the difference in ground state
free energies of S and P. The rate of the reaction is dependent on
the height of the free energy barrier between S and P. At the top
of this hump is the transition state. The transition state is not a
chemical species with any significant stability, and should not be
confused with a reaction intermediate. Rather it is a fleeting
molecular moment in which events such as bond breakage, bond
formation, and charge development have proceeded to the point at
which decay to either substrate or product is equally likely. The
difference between the energy levels of the ground state and the
transition state is the activation energy, ∆G‡. The rate of the
reaction is inversely and exponentially proportional to the value of
∆G‡.
Enzymes Affect Rxn Rates, Not Equilibria
(II)
Like other catalysts, enzymes enhance reaction rates by lowering
activation energies (Fig. 6-3). They have no effect on the position
of reaction equilibria. The example shown is for an enzyme which
follows the simple enzymatic steps of
E + S ⇄ ES ⇄ EP ⇄ E + P.
(E-enzyme; S-substrate; P-product; ES-transient complex
between the enzyme and substrate; EP-transient complex between
the enzyme and product). In the presence of the enzyme, three
peaks occur in the reaction coordinate diagram. Whichever peak is
the highest signifies the rate-limiting step of the overall reaction.
As discussed below, binding energy provided by the interaction of
the enzyme with the transition state contributes strongly to
lowering the activation energy of the reaction, and accelerating
its rate.
Relationship Between K’eq and ∆G’0
To describe the free energy changes for reactions, chemists define
a standard set of conditions (temperature 298˚K; partial pressure
of each gas = 1 atm; concentration of each solute 1 M) and
express the free energy change for a reacting system under these
conditions as ∆G0, the standard free energy change. Because
biochemical systems commonly have H+ concentrations far below 1
M, biochemists define a biochemical standard free energy change,
∆G’0, the standard free energy change at pH 7.0.
The equilibrium constant for a reaction (K’eq) under standard
biochemical conditions is mathematically linked to the standard free
energy change for a reaction, ∆G’0, via the equation
∆G’0 = -2.303 RT log K’eq.
In this equation, R is the gas constant,
8.315 J/mol.K, and T is the absolute
temperature, 298˚K (25˚C). The
numerical values for ∆G’0 as a function
of K’eq are tabulated in Table 6-4.
Note that a large negative value of
∆G’0 reflects a favorable equilibrium in
which the ratio of products to
reactants is much greater than 1/1.
Relationship Between ∆G‡ and Rxn Rate
The rate of a chemical reaction is determined by the concentration
of the reactant(s) and by a rate constant usually denoted by k. For
the unimolecular reaction S  P, the rate (or velocity) of the
reaction, V--representing the amount of S that reacts per unit
time--is expressed by a rate equation, V = k[S]. In this reaction,
the rate depends only on the concentration of S. This is a firstorder reaction. The factor k is a proportionality constant that
reflects the probability of a reaction under a given set of
conditions (pH, temperature, etc.). Here, k is a first-order rate
constant and has the units of reciprocal time (s-1). If a reaction
rate depends on the concentration of two different compounds, or
if the reaction is between two molecules of the same compound,
then the reaction is second-order and k is a second-order rate
constant, with units of M-1s-1. The rate equation then becomes V =
k[S1][S2]. From physical chemistry, it can be derived that the
magnitude of a rate constant is inversely and exponentially related
to the activation energy, ∆G‡. Thus, a lower activation energy
means a faster reaction rate.
Catalytic Power and Specificity of Enzymes
Enzymes commonly bring about enhancements in reaction rates in
the range of 5 to 17 orders of magnitude (Table 6-5). Enzymes
are also very specific, readily discriminating between substrates
with quite similar structures. The rate enhancements observed
for enzymes come from two distinct but interwoven parts. First,
catalytic functional groups on an enzyme react with a substrate
and lower the activation energy barrier for the reactions by
providing an alternative, lower-energy reaction path.
Second, noncovalent binding
interactions between the
substrate and enzyme release
a small amount of free energy
with each interaction that
helps lower the energy of the
transition state. The energy
derived from enzymesubstrate interaction is called
the binding energy, ∆GB.
Complementary Shapes of Enzymes and
Substrates
The active site of an enzyme has a
surface contour that is complementary in
shape to its substrate (and products).
This is illustrated for the two substrates
of the enzyme dihydrofolate reductase
in Fig. 6-4. Structural complementarity
is responsible for the high specificity of
enzyme reactions. The idea that the
enzyme and substrate are complementary
to one another was first proposed by the
organic chemist, Emil Fisher, in 1894.
He stated that the two components fit
together like a lock and key. This
proposal has greatly influenced the
development of biochemistry. However,
it is slightly misleading in that precise
complementarity between an enzyme and
its substrate would be counterproductive
to efficient catalysis. Later day
biochemical researchers instead realized
that the enzyme must be more
complementary to the reaction transition
state than to the substrate per se for
efficient catalysis to occur (next slide).
Transition State Complementarity Explains
Rate Enhancement (I)
The importance of transition state complementarity to rate
enhancement can be illustrated using an example of a hypothetical
“stickase” which catalyses the breakage of a metal stick, and
binds to the sick via magnetic interactions (Fig. 6-5). In the
uncatalyzed reaction, (Part a), the stick must first be bent to a
transition state structure before being broken. Due to the high
activation energy barrier of the bent stick transition state, the
overall reaction (which has a negative free energy change) is
relatively slow. If the stickase
were precisely complementary to
the metal bar (Part b), the rate
of the reaction would not be
improved as the enzyme actually
would stabilize the structure of
the stick. Under these
conditions, the ES complex
corresponds to a trough in the
reaction coordinate diagram from
which the substrate would have
difficulty escaping. (Continued on
the next slide).
Transition State Complementarity Explains
Rate Enhancement (II)
However, if the stickase were
more complementary to the
transition state of the
reaction (Part c), then the
increase in free energy
required to draw the stick
into a bent and partially
broken conformation would be
offset, or paid for, by the
magnetic interactions (binding
energy) between the enzyme
and the substrate in its
transition state. This energy
payment translates into a
lower net activation energy
and a faster reaction rate.
Transition State Complementarity Explains
Rate Enhancement (III)
Real enzymes work on an analogous
principle. Some weak interactions are
formed in the ES complex, but the full
complement of such interactions between
the substrate and enzyme is formed only
when the substrate reaches the transition
state. The free energy (binding energy)
released by the formation of these
interactions partially offsets the energy
required to reach the top of the energy
hill. The summation of the unfavorable
(positive) activation energy ∆G‡ and the
favorable (negative) binding energy ∆GB
results in a lower net activation energy
(Fig. 6-6). Even on the enzyme, the
transition state is not a stable species but
is a brief point in time that the substrate
spends atop an energy hill. The enzymecatalyzed reaction is much faster than the
uncatalyzed process because the hill is much
smaller. The important point is that weak
binding interactions between the enzyme
and the substrate provide a substantial
driving force for enzymatic catalysis.
Contributions of Binding Energy to Reaction
Specificity and Catalysis (I)
For a reaction to take place, significant physical and
thermodynamic factors contributing to ∆G‡ must be overcome.
These include 1) the entropy (freedom of motion) of molecules in
solution, which reduces the possibility that they will react
together, 2) the solvation shell of hydrogen-bonded water
molecules that surrounds and helps to stabilize most biomolecules
in solution, 3) the distortion of substrates that must occur in
many reactions, and 4) the need for proper alignment of
catalytic functional groups on the enzyme. All of these factors
can be overcome due to the binding energy released on
interaction of the enzyme with the transition state, as explained
in the next slide. Binding energy also gives an enzyme its
specificity, which is the ability of an enzyme to discriminate
between its substrate and a competing molecule with a similar
structure.
Contributions of Binding Energy to Reaction
Specificity and Catalysis (II)
The mechanism by which binding energy compensates for physical
and thermodynamic factors that impede reaction rates are as
follows. 1) Entropy reduction: The restriction in the motions of
two substrates that are about to react is one benefit of binding
them to an enzyme. Binding energy holds the substrates in the
proper orientation to react--a substantial contribution to
catalysis, because productive collisions between molecules in
solution can be exceedingly rare.
Studies have shown that constraining
the motion of two reactants can
produce rate enhancements of many
orders of magnitude (Fig. 6-7). 2)
Desolvation: Formation of weak bonds
between the enzyme and substrate
results in the desolvation of the
substrate. The removal of bound
water molecules from the substrate
removes water molecules which
otherwise might impede the reaction.
Contributions of Binding Energy to Reaction
Specificity and Catalysis (III)
3) Substrate distortion: Binding energy involving weak interactions
formed only in the reaction transition state helps to compensate
thermodynamically for any distortion, primarily electronic
redistribution, that the substrate must undergo to react. 4)
Catalytic group alignment: Enzymes typically undergo changes in
conformation when the substrate binds that are induced by
multiple weak interactions with the substrate. The alignment of
catalytic functional groups is referred to as induced fit, and it
serves to bring specific functional groups on the enzyme into the
proper position to catalyze the reaction.
Other Contributions to Enzyme Catalysis:
General Acid-base Catalysis
Many biochemical reactions involve the formation of unstable
charged intermediates that tend to break down rapidly to their
constituent reactant species, thus slowing the reaction (Fig. 6-8).
Charged intermediates can often be stabilized by the transfer of
protons to or from the substrate or intermediate to form a species
that breaks down more readily to products. Catalysis, such as in
organic chemistry reactions, that uses only the H+ or OH- ions
present in solution is referred to a specific acid-base catalysis.
Proton transfers mediated by weak acids and bases other than
water, such as the functional groups in the side-chains of amino
acids, is referred to as general-acid base catalysis. Amino acid
side-chains that are commonly involved in general acid-base
catalysis are listed in Fig. 6-9.
Other Contributions to Enzyme Catalysis:
Covalent Catalysis
In covalent catalysis, a transient covalent bond is formed
between the enzyme and the substrate. Consider the hydrolysis
of a bond between groups A and B:
A-B + H2O  A + B
In the presence of a covalent catalyst (an enzyme with the
nucleophilic group X:) the reaction becomes
1) A-B + X:  A-X + B
2) A-X + H2O  A + X:
This alters the pathway of the reaction, and it results in
catalysis if the new pathway has a lower activation energy than
the uncatalyzed pathway. Both of the new steps must be faster
than the uncatalyzed reaction. A number of amino acid sidechains, including all of those in Fig. 6-9, and the functional
groups of some enzyme cofactors can serve as nucleophiles in the
formation of covalent bonds with substrates. These covalent
complexes always undergo further reaction to regenerate the
free enzyme.
Other Contributions to Enzyme Catalysis:
Metal Ion Catalysis
Metals, whether tightly bound to the enzyme or taken up from
solution along with the substrate, can participate in catalysis in
several ways. Ionic interactions between an enzyme-bound metal
and a substrate can help orient the substrate for reaction or
stabilize charged reaction transition states. This use of weak
binding interactions between metal and substrate is similar to
some of the uses of enzyme-substrate binding energy described
earlier. Metals can also mediate oxidation-reduction reactions by
reversible changes in the metal ion’s oxidation state. Nearly a
third of all enzymes require one or more metal ions for catalytic
activity.
Intro to Enzyme Kinetics
The oldest approach to understanding enzyme mechanisms, and the
one that remains the most important, is to determine the rate of
a reaction and how it changes in response to changes in
experimental parameters. This is the discipline known as enzyme
kinetics. A key factor affecting the rate of a reaction catalyzed
by an enzyme is the concentration of substrate, [S]. Studying the
effects of substrate concentration is complicated by the fact that
[S] changes during the course of an in vitro reaction as substrate
is converted to product. One simplifying approach in kinetic
experiments is to measure the initial rate (initial velocity),
designated V0 (Fig. 6-10). In a typical reaction, the enzyme may
be present in nanomolar quantities,
whereas [S] may be five or six orders of
magnitude higher. If only the beginning
of the reaction is monitored (often the
first 60 seconds or less), changes in [S]
therefore can be limited to a few
percent, and [S] can be regarded as
constant. V0 then can be examined as a
function of [S] which is adjusted using
several reactions.
Effect of Substrate Concentration on
Reaction Rate
The effect on V0 of varying [S] when the enzyme concentration is
held constant is shown in Fig. 6-11. This is the appearance of a
V0 vs [S] kinetic plot for a typical enzyme. At relatively low
concentrations of substrate, V0 increases almost linearly with an
increase in [S]. At higher substrate concentrations, V0 increases
by smaller and smaller amounts in response to increases in [S].
Finally, a point is reached beyond which increases in V0 are
vanishingly small as [S] increases. This plateau-like V0 region is
close to the maximum velocity, Vmax.
The Role of the ES Complex (I)
The ES complex is the key to understanding the kinetic behavior of an
enzyme. In 1913, Leonor Michaelis and Maud Menten, developed a kinetic
equation to explain the behavior of many simple enzymes. Key to the
development of their equation, is the assumption that the enzyme first
combines with its substrate to form an enzyme-substrate complex in a
relatively fast reversible step:
k1
E + S
⇄
ES
k-1
The ES complex then breaks down in a slower second step to yield the
free enzyme and the reaction product P:
k2
ES
⇄
E + P
k-2
If the slower second reaction limits the rate of the overall reaction, the
overall rate must be proportional to the concentration of the species that
reacts in the second step, i.e., ES.
At any given instant in an enzyme-catalyzed reaction, the enzyme exists
in two forms, the free or uncombined form E and the combined form ES.
At low [S], most of the enzyme is in the uncombined E form. Here, the
rate is proportional to [S] because the direction of the first equation
above is pushed toward formation of more ES as [S] increases.
(Continued on the next slide).
The Role of the ES Complex (II)
The maximum initial rate of the catalyzed reaction (Vmax) is
observed when virtually all of the enzyme is present in the ES
complex and [E] is vanishingly small. Under these conditions, the
enzyme is saturated with its substrate, so that further increases
in [S] have no effect on rate. This condition exists when [S] is
sufficiently high that essentially all the free enzyme has been
converted to the ES form. The saturation effect is a
distinguishing characteristic of enzymatic catalysts and is
responsible for the plateau observed in Fig. 6-11. The pattern
seen in that figure is sometimes referred to as saturation
kinetics.
When the enzyme is first mixed with a large excess of substrate,
there is an initial period, the pre-steady state, during which the
concentration of ES builds up. This period is usually too short to
be easily observed, lasting just microseconds, and is not evident in
Fig. 6-10. The reaction quickly achieves a steady state in which
[ES] remains approximately constant over time. The measured V0
generally reflects the steady state, even though V0 is limited to
the early part of the reaction. The analysis of these initial rates
is referred to as steady-state kinetics.
Derivation of the MM Equation (I)
The kinetic curves expressing the relationship between V0 and [S]
have the same general shape (a rectangular hyperbola) for most
enzymes, which can be expressed algebraically by the MM equation.
Michaelis and Menten derived this equation starting from their
basic hypothesis that the rate-limiting step in enzymatic reactions
is the breakdown of the ES complex to product and free enzyme.
The MM equation is
V0 = Vmax[S]/(Km + [S]).
All these terms, [S], V0, Vmax, as well as the constant called the
Michaelis constant, Km, can be readily measured experimentally.
The derivation of the MM equation starts with the two basic steps
of the formation and breakdown of ES. Early in the reaction, the
concentration of the product [P] is negligible, and a simplifying
assumption is made that the reaction P  S (described by k-2) can
be ignored. The overall reaction then reduces to
k1
k2
E + S ⇄ ES  E + P.
k-1
Derivation of the MM Equation (II)
V0 is determined by the breakdown of ES to form product, which
is determined by [ES] through the equation
V0 = k2[ES].
Because [ES] in the above equation is not easily measured
experimentally, an alternative expression for this term must be
found. First, the term [Et], representing the total enzyme
concentration (the sum of free and substrate-bound enzyme) is
introduced. Free or unbound enzyme [E] can then be represented
by [Et] - [ES]. Also, because [S] is ordinarily far greater than
[Et], the amount of substrate bound by the enzyme at any given
time is negligible compared with the total [S]. With these
conditions in mind, the following steps lead to an expression for V0
in terms of easily measurable parameters.
Derivation of the MM Equation (III)
Derivation of the MM Equation (IV)
Derivation of the MM Equation (V)
The MM equation describes the kinetic behavior of a great many
enzymes, and all enzymes that exhibit a hyperbolic dependence of
V0 on [S] are said to follow Michaelis-Menten kinetics. However
the MM equation does not depend on the relatively simple twostep reaction mechanism discussed above. Many enzymes that
follow MM kinetics have quite different mechanisms, and enzymes
that catalyze reactions with six or eight identifiable steps often
exhibit the same steady-state kinetic behavior. Even though the
MM equation holds true for many enzymes, both the magnitude
and the real meaning of Vmax and Km can differ from one enzyme
to another. This is an important limitation of the steady-state
approach to enzyme kinetics.
Validation of the MM Equation
The MM equation can be shown to correctly explain the V0 vs [S]
curves of many enzymes by considering limiting situations where [S]
is very high or very low (Fig. 6-12). At low [S], Km >> [S] and the
[S] term in the denominator of the MM equation becomes
insignificant. The equation simplifies to V0 = Vmax[S]/Km and V0
exhibits a linear dependence on [S], as is observed at the left side
of V0 vs [S] graphs. At high [S], where [S] >> Km, the Km term in
the denominator of the MM equation becomes insignificant and the
equation simplifies to V0 = Vmax. This is consistent with the plateau
in V0 observed at high [S] in kinetic graphs.
An important numerical relationship emerges from the MM equation
in the special case when V0 is exactly one-half Vmax. Here
Vmax/2 = Vmax[S]/(Km + [S]).
On dividing by Vmax, the equation is
1/2 = [S]/(Km + [S]).
After solving for Km, we get
Km + [S] = 2[S], or Km = [S].
This is a very useful, practical
definition of Km. Km is equivalent to
the substrate concentration at which
V0 is one-half Vmax.
Double-reciprocal Plots
Because the plot of V0 vs [S] for an enzyme-catalyzed reaction
asymptotically approaches the value of Vmax at high [S], it is
difficult to accurately determine Vmax (and thereby, Km) from such
graphs. The problem is readily solved by converting the MichaelisMenten kinetic equation to the so-called double-reciprocal equation
(Lineweaver-Burk equation) which describes a linear plot from which
Vmax and Km can be easily obtained (Box 6-1, Fig. 1). The
Lineweaver-Burk equation is derived by first taking the reciprocal of
both sides of the Michaelis-Menten equation
1/V0 = (Km + [S])/Vmax[S]
Separating the components of the
numerator on the right side of the
equation gives
1/V0 = Km/Vmax[S] + [S]/Vmax[S]
Which simplifies to
1/V0 = Km/Vmax[S] + 1/Vmax.
The plot of 1/V0 vs 1/[S] gives a
straight line, the y-intercept of which
is 1/Vmax and the x-intercept of which
is -1/Km.
The Meaning of the Km
The Km can vary greatly from enzyme to enzyme, and even for
different substrates of the same enzyme (Table 6-6). The Km is
sometimes used (often inappropriately) as an indicator of the
affinity of an enzyme for its substrate. The actual meaning of
the Km depends on specific aspects of the reaction mechanism
such as the number and relative rates of the individual steps. For
example, for a reaction with two steps, Km = (k2 + k-1)/k1. If k2
is actually rate-limiting, then k2 << k-1, and Km reduces to k-1/k1,
which is the dissociation constant, Kd of the ES complex. Where
these conditions hold, Km does represent a measure of the affinity
of the enzyme for its substrate. However this scenario often
doesn’t apply for an enzyme due to variances in the contributions
of individual rate constants to the overall reaction rate. Thus Km
cannot always be considered a simple measure of the affinity of
an enzyme for its substrate.
Information Derived from Vmax
The meaning of the quantity Vmax also varies greatly from one
enzyme to the next. If an enzyme reacts via the two-step MM
mechanism, then Vmax = k2[Et]. However, the number of reaction
steps and the identity of the rate-limiting step can vary from
enzyme to enzyme. Therefore, it is useful to define a more general
rate constant, kcat, to describe the rate constant of the rate
limiting step(s) of any enzyme-catalyzed reaction at saturation.
With the modification that Vmax = kcat[Et], the MM equation becomes
V0 = kcat[Et][S]/(Km + [S]).
The constant kcat is a first-order rate constant and hence has the
units of reciprocal time (s-1). It is also called the turnover number
for the enzyme-catalyzed reaction. It is equivalent to the number of
substrate molecules converted to product in a given unit of time on a
single enzyme molecule when the enzyme is saturated with substrate.
The turnover numbers of several enzymes are listed in Table 6-7.
The Specificity Constant (kcat/Km)
Together, the parameters kcat and Km can be used to evaluate the
catalytic efficiency of an enzyme. The best way to determine the
catalytic efficiency of an enzyme is to determine the ratio of kcat/Km
for its reaction. This parameter, sometimes called the specificity
constant, is the rate constant for the conversion of E + S to E + P.
When [S] << Km, the previous MM equation form converts to
V0 = (kcat/Km)([Et][S]).
V0 in this case depends on the concentration of two reactants, [Et]
and [S]. Therefore, this is a second-order rate equation and the
constant kcat/Km is a second-order rate constant with the units M-1s1. There is an upper limit to k
cat/Km, imposed by the rate at which E
and S can diffuse together in an aqueous solution. This diffusioncontrolled limit is 108 to 109 M-1s-1, and many enzymes have a
kcat/Km near this range (Table 6-8). Such enzymes are said to have
achieved catalytic perfection.
Bisubstrate Reactions
In most enzymatic reactions, two or more different substrate
molecules bind to an enzyme and participate in the reaction. The
rates of such bisubstrate reactions can also be analyzed by the MM
approach (Fig. 6-14, not covered). Reactions with two substrates
usually involve transfer of an atom or a functional group from one
substrate to the other. These reactions can proceed by several
different pathways. In some cases, both substrates are bound to
the enzyme concurrently at some point in the course of the
reaction, forming a noncovalent ternary complex (Fig. 6-13a). As
noted in the figure, the substrates can bind in a random sequence
or in a specific order. In other cases, the first substrate is
converted to product and dissociates before the second substrate
binds, so no ternary complex is formed. An example of this is the
Ping-Pong, or double-displacement, mechanism (Fig. 6-13b). In
these reactions, a functional group often is transferred from the
first substrate to the second.
Intro. to Enzyme Inhibition
Enzyme inhibitors are molecules that interfere with catalysis,
slowing or halting enzymatic reactions. Enzyme inhibitors are among
the most important pharmaceutical agents known. For example,
aspirin (acetylsalicylate) inhibits the enzyme that catalyzes the
first step in the synthesis of prostaglandins, compounds involved in
many processes, including some that cause pain. The study of
enzyme inhibitors also has provided valuable information about
enzyme mechanisms and has helped define metabolic pathways.
There are two broad classes of enzyme inhibitors: reversible and
irreversible inhibitors.
Competitive Inhibition (I)
One example of reversible enzyme inhibition will be covered:
competitive inhibition (Fig. 6-15a). A competitive inhibitor (I)
competes with the substrate for binding to the active site of an
enzyme. While the inhibitor occupies the active site, it prevents
the binding of the substrate to the enzyme and blocks the
reaction. Many competitive inhibitors are structurally similar to the
substrate and combine with the enzyme to form an EI complex,
but without leading to catalysis. Competitive inhibition can be
analyzed quantitatively by steady-state kinetics. In the presence
of a competitive inhibitor, the MM equation becomes
V0 = Vmax[S]/(Km + [S])
Where
 = 1 + [I]/KI and KI = [E][I]/[EI].
The experimentally determined
variable Km, the Km observed in the
presence of the competitive inhibitor,
is often called the “apparent” Km.
Competitive Inhibition (II)
Because a competitive inhibitor binds
reversibly to an enzyme, the competition
can be biased to favor the substrate
simply by adding more substrate to the
reaction. When [S] far exceeds [I], the
probability that an inhibitor will bind to
the enzyme is minimized and the reaction
exhibits a normal Vmax. However, the [S]
at which V0 = 1/2 Vmax, the apparent
Km, increases in the presence of inhibitor
by the factor . This affect on
apparent Km, combined with the absence
of an effect on Vmax, is diagnostic of
competitive inhibition and is readily
revealed in a double-reciprocal kinetic
plot (Box 6-2. Fig. 1). The equilibrium
constant for inhibitor binding, KI, can
also be obtained from these plots. Many
drugs act by competitively inhibiting
enzymes (e.g., ibuprofen and the
cyclooxygenase enzymes, COX 1 & 2).
Irreversible Inhibition
Irreversible inhibitors bind covalently
to or destroy a functional group on an
enzyme that is essential for the
enzyme’s activity. They also can
inhibit an enzyme by forming a
particularly stable noncovalent
association with the enzyme. An
example of a irreversible covalent
inhibitor of the protease,
chymotrypsin, is shown in Fig. 6-16.
As we will discuss in the next lecture
slide file, chymotrypsin contains a
reactive serine residue in its active
site that is intimately involved in
catalysis of peptide bond cleavage.
This serine will react with the
inhibitor diisopropylfluorophosphate
(DIFP) which modifies the serine
residue irreversibly, and thereby
inhibits the proteolytic activity of the
enzyme. In contrast to ibuprofen,
aspirin is a covalent irreversible
inhibitor of COX enzymes.
Mechanism-based Inactivators
A special class of irreversible inhibitors are the mechanism-based
(suicide) inactivators. These compounds are relatively unreactive
until they bind to the active site of a specific enzyme. A suicide
inactivator undergoes the first few chemical steps of the normal
enzymatic reaction, but instead of being transformed into the
normal product, the inactivator is converted into a very reactive
compound that combines irreversibly with the enzyme. These
inhibitors earn their name because they hijack the normal enzyme
reaction mechanism to inactivate the enzyme. Because drugs that
serve as mechanism-based inactivators are highly specific for their
target enzymes, they often have the advantage of few side
effects. An example of a mechanism-based inhibitor that is used
in the treatment of the disease, trypanosomiasis, is presented in
Box 6-3 (not covered).
Transition-state Analogs
An irreversible enzyme inhibitor need not
bind covalently to an enzyme if
noncovalent binding is so tight that the
inhibitor dissociates only rarely. Such
inhibitors commonly resemble the
predicted transition state structure of
the reaction and are called transitionstate analogs. These compounds bind
more tightly to an enzyme than the
substrate because they fit into the
active site better. For example,
transition state analogs designed to
inhibit the glycolytic enzyme aldolase bind
to that enzyme more than four order of
magnitude more tightly than its actual
substrates (Fig. 6-17). Observations
that such molecules are effectively
irreversible inhibitors of enzymes,
support the concept that enzyme active
sites are most complementary to that of
the transition state of the reaction.
Lastly, anti-HIV drugs that inhibit the
required protease function of the virus
are actually transition-state analogs.
Enzyme pH-activity Profiles
Enzymes have an optimum pH at which their activity is maximal.
At higher or lower pH values, their activity declines (Fig. 6-18).
This is because ionizable amino acid side-chains that are
important for catalysis of the reaction, or maintain the structure
of the enzyme, must maintain a certain state of ionization to
function properly. The pH range over which an enzyme undergoes
changes in activity can provide a clue as to the type of amino acid
residue involved in catalysis. A change in activity near pH 7.0, for
example, often reflects titration of a His residue. However, the
effects of pH on activity must be interpreted cautiously, as in the
closely packed environment of a protein, the pKa of an amino acid
side-chain can vary significantly from the pKa of the free amino
acid in solution. The pH optimum for the activity of an enzyme
generally is close to that of the pH of the environment in which
the enzyme normally functions. For example, the pH optimum of
pepsin, a gastric digestive enzyme, is about 1.6. The pH optimum
of the cytoplasmic enzyme, glucose 6-phosphatase, of hepatocytes
is about 7.8.