Download From coherent to quantum atom optics

Hanbury Brown and Twiss
and other correlations:
from photon to atom quantum optics
Sao Carlos, June 4, 2011
Alain Aspect - Groupe d’Optique Atomique
Institut d’Optique – Palaiseau
http://www.lcf.institutoptique.fr/atomoptic
1
The Hanbury Brown and Twiss effect
and other landmarks in quantum optics:
from photons to atoms
• The Hanbury Brown and Twiss photon-photon
correlation experiment: a landmark in quantum optics
• Atomic HBT with He*
• Pairs of quantum correlated atoms in spontaneous
4-wave mixing of matter waves
2
The Hanbury Brown and Twiss effect
and other landmarks in quantum optics:
from photons to atoms
• The Hanbury Brown and Twiss photon-photon
correlation experiment: a landmark in quantum optics
• Atomic HBT with He*
• Pairs of quantum correlated atoms in spontaneous
4-wave mixing of matter waves
3
The HB&T experiment: correlations in light?
Measurement of the correlation
function of the photocurrents at
two different points and times
g (r1 , r2 ; ) 
(2)
i (r1 , t ) i (r2 , t   )
i (r1 , t ) i (r2 , t )
Semi-classical model of the
photodetection (classical em field,
quantized detector):
Measure of the correlation
function of the light intensity:
i (r, t )  I (r, t )  E(r, t )
2
4
The HB&T effect: correlations in light!
Light from incoherent source: time and space correlations
Mj

P1
P1
P2
P2
g (2)(2)
(r2  r1;  0)  1
g (r1  r2 ; )  1
))
r,11r2,,;rr22;;0)
ggg (r(1(r
(2)
(2)
(2)
2
2
11
c
Lc
r1 – r2
g (2) (r1  r2 ;  0)  2
g (2) (r1  r2
Lc ;
c) 1
A measurement of g(2) 1 vs.  and
r1r2 yields the coherence volume
• time coherence
 c  1/ 
• space coherence
Lc   / 
5
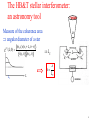
The HB&T stellar interferometer:
an astronomy tool

Measure of the coherence area
 angular diameter of a star
g ( L;0) 
(2)
i (r1 , t ) i (r1  L, t   )
i (r1 , t ) i (r2 , t )
 LC

Lc
L
L

LC
6
The HB&T stellar interferometer:
an astronomy tool

Measure of the coherence area
 angular diameter of a star
g ( L;0) 
(2)
i (r1 , t ) i (r1  L, t   )
 LC
i (r1 , t ) i (r2 , t )

Lc
L
L

LC
Equivalent to the Michelson stellar interferometer ?
Visibility
of fringes
g (1) (r1 , r2 ; ) 
E(r1 , t ) E(r2 , t   )
E(r1 , t )
2 1/ 2
E(r2 , t   )
2 1/ 2
r1
r
r2
7
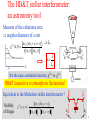
The HB&T stellar interferometer:
an astronomy tool
Measure of the coherence area
 angular diameter of a star
g ( L;0) 
(2)
i (r1 , t ) i (r1  L, t   )

 LC
i (r1 , t ) i (r2 , t )

Lc
L
L

LC
Not the same correlation function: g(2) vs g(1)
HB&T insensitive to atmospheric fluctuations!
Equivalent to the Michelson stellar interferometer ?
Visibility
of fringes
g (1) (r1 , r2 ; ) 
E(r1 , t ) E(r2 , t   )
E(r1 , t )
2 1/ 2
E(r2 , t   )
2 1/ 2
r1
r
r2
8
HBT and Michelson stellar interferometers
yield the same quantity
Many independent random
emitters: complex electric field
= sum of many independent
random processes
P1
Mj
g (2) (r1 , r2 ; )
P2
j


E( P, t )   a j exp  j 
M j P   jt 
c
j


Incoherent source
Central limit theorem
 Gaussian random process
g (r1 , r2 ; ) 
(1)
E* (r1 , t ) E(r2 , t   )
E(r1 , t )
g (2) (r1 , r2 ; ) 
2
1/ 2
E(r2 , t  t )
i (r1 , t ) i (r2 , t   )
i (r1 , t ) i (r2 , t )

2
1/ 2
g (r1 , r2 ; )  1  g (r1 , r2 ; )
(2)
(1)
Michelson Stellar
Interferometer
Same width:
 star size
E* (r1 , t ) E(r1 , t )E* (r2 , t   ) E(r2 , t   )
E(r1 , t )
2
E(r2 , t   )
2
2
HBT Stellar
Interferometer
9
The HB&T stellar interferometer:
it works!
The installation at Narrabri
(Australia): it works!
HB et al.,
1967
10
HBT intensity correlations:
classical or quantum?
HBT correlations were predicted, observed, and used to
measure star angular diameters, 50 years ago. Why bother?
The question of their interpretation, classical vs. quantum,
provoked a debate that prompted the emergence of modern
quantum optics!
11
Classical wave explanation for HB&T correlations (1):
Gaussian intensity fluctuations in incoherent light
Mj
Many independent random emitters:
complex electric field fluctuates
 intensity fluctuates
P1
g (2) (r1 , r2 ; )
P2
I (t )  I (t )  g (2) (r1 , r1;0)  1
2
Gaussian random process 
2
g (r1 , r2 ; )  1  g (r1 , r2 ; )
(2)
(1)
2
For an incoherent source, intensity fluctuations (second order
coherence function) are related to first order coherence function
12
Classical wave explanation for HB&T correlations (2):
optical speckle in light from an incoherent source
Mj
Many independent random
emitters: complex electric field
= sum of many independent
random processes
P1
g (2) (r1 , r2 ; )

P2
Gaussian random process 
j


E( P, t )   a j exp  j 
M j P   jt 
c
j


g (r1 , r2 ; )  1  g (r1 , r2 ; )
(2)
(1)
2
Intensity pattern (speckle) in the
observation plane:
• Correlation radius Lc   / 
• Changes after c  1 / 
13
The HB&T effect with photons: a hot debate
Strong negative reactions to the HB&T proposal (1955)
In term of photon counting
Mj
P1
P2
g (2) (r1 , r2 ; )
joint detection probability
 (r1 , r2 ; t , t   )
g (r1 , r2 ; ) 
 (r1 , t )  (r2 , t )
(2)
single detection probabilities
For independent detection events g(2) = 1
g(2)(0) = 2  probability to find two photons at the same place
larger than the product of simple probabilities: bunching
How might independent particles be bunched ?
14
The HB&T effect with photons: a hot debate
Strong negative reactions to the HB&T proposal (1955)
Mj
P1
g (2) (r1 , r2 ; )
P2
g(2)(0) > 1  photon bunching
How might photons emitted from
distant points in an incoherent source
not be statistically independent?
HB&T answers • Experimental demonstration!
• Light is both wave and particles.
g (r1 , r2 ; )  1  g (r1 , r2 ; )
(2)
(1)
2
Uncorrelated detections easily understood as independent particles
(shot noise)
Correlations (excess noise) due to beat notes of random waves
cf . Einstein’s discussion of wave particle duality in Salzburg (1909),
about black body radiation fluctuations
15
The HB&T effect with photons:
Fano-Glauber quantum interpretation
Two photon emitters, two detectors
E1
E2
D1

D2
Initial state:
•Emitters excited
•Detectors in ground state

E1
E2
D1
D2
Final state:
•Emitters in ground state
•Detectors ionized
Two paths to go from THE initial
state to THE final state
Amplitudes of the two process interfere   (r1 , r2 , t )   (r1 , t )   (r2 , t )
Incoherent addition of many interferences: factor of 2 (Gaussian process)
16
The HB&T effect with particles: a non
trivial quantum effect
Two paths to go from one initial state
to one final state: quantum interference
of two-photon amplitudes
Two photon interference effect: quantum weirdness
• happens in configuration space, not in real space
• A precursor of entanglement (violation of Bell inequalities), HOM, etc…
Lack of statistical independence (bunching) although no “real” interaction
cf. Bose-Einstein Condensation (letter from Einstein to Schrödinger, 1924)
Two entangled particles interference effect, and the ability to prepare and
observe individual pairs, is at the root of the second quantum revolution*
*AA: “John Bell and the second quantum revolution” foreword of “Speakable and
Unspeakable in Quantum Mechanics” , J.S. Bell (Cambridge University Press 2004);
http://www.lcf.institutoptique.fr/Groupes-de-recherche/Optique-atomique/Membres/
17
Intensity correlations in laser light?
yet more hot discussions!
Phys Rev Lett 1963
1960: invention of the laser (Maiman, Ruby laser)
•1961: Mandel & Wolf: HB&T bunching effect should be easy
to observe with a laser: many photons per mode
•1963: Glauber: laser light should NOT be bunched:
 quantum theory of coherence
(8 Juillet
1960, New York Times)
•1965: Armstrong: experiment with single mode
AsGa
laser: no bunching well above threshold; bunching
below threshold
•1966: Arecchi: similar with He Ne laser: plot of g(2)()
Simple classical model for laser light:
E  E0 exp{i t  0 }  en
en
E0
Quantum description identical by
use of Glauber-Sudarshan P
representation (coherent states )
18
The Hanbury Brown and Twiss effect:
a landmark in quantum optics
• Easy to understand if light is described as an
electromagnetic wave
• Subtle quantum effect if light is described as made of
photons
Intriguing quantum effect for particles*
Hanbury Brown and Twiss effect with atoms?
* See G. Baym, Acta Physica Polonica (1998) for HBT with high energy particles
19
Atomic Hanbury Brown and Twiss and
other quantum atom optics effects
• The Hanbury Brown and Twiss photon-photon
correlation experiment: a landmark in quantum optics
• Atom atom correlation experiments: He* fantastic
• Pairs of quantum correlated atoms by spontaneous
non-linear mixing of 4 de Broglie waves
20
The HB&T effect with atoms:
Yasuda and Shimizu, 1996
• Cold neon atoms in a MOT (100 mK) continuously
pumped into an untrapped (falling) metastable state
Single atom detection (metastable atom)
Narrow source (<100mm): coherence volume
as large as detector viewed through diverging
lens: no reduction of the visibility of the bump
Effect clearly seen
•Bump disappears when
detector size >> LC
•Coherence time as
predicted: / E  0.2 ms
Totally analogous to HB&T: continuous atomic beam
21
Atomic density correlation (“noise correlation”):
a new tool to investigate quantum gases
3 atoms collision rate enhancement in a thermal gas, compared to a BEC
• Factor of 6 ( n3 (r)  3! n(r) ) observed (JILA, 1997) as predicted by
Kagan, Svistunov, Shlyapnikov, JETP lett (1985)
3
Interaction energy of a sample of cold atoms
•
•
n 2 (r)  2 n(r)
2
n 2 (r)  n(r)
2
for a thermal gas (MIT, 1997)
for a quasicondensate (Institut d’Optique, 2003)
Noise correlation in absorption images of a sample of cold atoms (as
proposed by Altmann, Demler and Lukin, 2004)
•Correlations in a quasicondensate (Ertmer, Hannover 2003)
•Correlations in the atom density fluctuations of cold atomic samples
Atoms released from a Mott phase (I Bloch, Mainz, 2005)
Molecules dissociation (D Jin et al., Boulder, 2005)
Fluctuations on an atom chip (J. Estève et al.,Institut d’Optique, 2005)
… (Inguscio, …)
22
Atomic density correlation (“noise correlation”):
a new tool to investigate quantum gases
3 atoms collision rate enhancement in a thermal gas, compared to a BEC
• Factor of 6 ( n3 (r)  3! n(r) ) observed (JILA, 1997) as predicted by
Kagan, Svistunov, Shlyapnikov, JETP lett (1985)
3
Interaction energy of a sample of cold atoms
•
•
n 2 (r)  2 n(r)
2
n 2 (r)  n(r)
2
for a thermal gas (MIT, 1997)
for a quasicondensate (Institut d’Optique, 2003)
Noise correlation in absorption images of a sample of cold atoms (as
proposed by Altmann, Demler and Lukin, 2004)
Measurements of atomic density averaged over small volumes
What about individual atoms
correlation function measurements?
23
The Hanbury Brown and Twiss effect
and other landmarks in quantum optics:
from photons to atoms
• The Hanbury Brown and Twiss photon-photon
correlation experiment: a landmark in quantum optics
• Atomic HBT with He*
• Pairs of quantum correlated atoms in spontaneous
4-wave mixing of matter waves
24
Metastable Helium 2 3S1
An unique atomic species
• Triplet () 2 3S1 cannot radiatively decay
to singlet () 1 1S0 (lifetime 9000 s)
• Laser manipulation on closed transition
2 3S1  2 3P2 at 1.08 mm (lifetime 100 ns)
2 3P2
1.08 mm
2 3S1
• Large electronic energy stored in He*
 ionization of colliding atoms or
molecules
19.8 eV
 extraction of electron from metal:
single atom detection with
Micro Channel Plate detector
Similar techniques in Canberra, Amsterdam, ENS
1 1S0
25
He* laser cooling and trapping,
and MCP detection: unique tools
Clover leaf trap
@ 240 A :
B0 : 0.3 to 200 G ;
B’ = 90 G / cm ; B’’= 200 G / cm2
z / 2 = 50 Hz ;  / 2 = 1800 Hz
He* on the Micro Channel Plate
detector:
 an electron is extracted
 multiplication
 observable pulse
Single atom detection of He*
Analogue of single photon counting development, in the early 50’s
Tools crucial to the discovery of He* BEC (Institut d’Optique, 2000)
26
Position and time resolved detector:
a tool for atom correlation experiments
Delay lines + Time to digital
converters: detection events
localized in time and position
• Time resolution better than
1 ns 
• Dead time : 30 ns 
• Local flux limited by MCP
saturation 
• Position resolution (limited
by TDC): 200 mm 
105 single atom detectors working in parallel !      
27
Atom atom correlations
in an ultra-cold atom cloud
Cold
sample
y
x
z
• Cool the trapped sample to a chosen
temperature (above BEC transition)
• Release onto the detector
• Monitor and record each detection
event n:
Detector
Pixel number in (coordinates x, y)
Time of detection tn (coordinate z)
 i1 , t1  ,...  in , tn  ,..
i , t  ,...i , t  ,... = a record
1
1
n
n
of the atom positions in a single cloud
Repeat many times (accumulate records) at same temperature
Pulsed experiment: 3 dimensions are equivalent ≠ Shimizu experiment
28
g(2) correlation function:
4He* thermal sample (above T
BEC)
• For a given record (ensemble of
detection events for a given
released sample), evaluate
probability of a pair of atoms
separated by x, y, z.
 [(2)(x, y, z)]i
• Average over many records (at
same temperature)
• Normalize by the autocorrelation
of average (over all records)
 g (2) (x, y, z )
 HBT bump around x = y = z = 0
g (x  y  0; z )
(2)
1.3 mK
Bump visibility = 5 x 10-2
Agreement with prediction
(resolution)
29
The detector resolution issue
xdet
If the detector resolution xdet is larger than the HBT
bump width Lcx
Lcx
2 M xsource
tfall
(2)
then the height of the HB&T bump is reduced: g  1
LC
1
xdet
• ysource = zsource 4 mm  Lcy = Lcz =500 mm 
• xsource  150 mm  Lcy = 13 mm 
At 1 mK,
g (2) (x, y, z )
y
x
z
Resolution (200 mm) sufficient along y and z but
insufficient along x. Expected reduction factor of 15
NB: vertical resolution is more than sufficient: zdet  V t  1 nm 
30
x,y correlation function (thermal 4He*)
Various source sizes
g (x; y; 0)
( 2)
1.3 mK
x
0.55 mK
x
y
1.0 mK
y
g(2)(x, x, x) :
pancake perpendicular
to x (long dimension
x
of the source)
1.35 mK
31
g(2) correlation function in a
Bose Einstein Condensate of 4He* (T < Tc)
Decrease the atomic cloud
temperature:
phase transition to BEC
g (2) (0;0;0)  1
No bunching: analogous to
laser light
(see also Öttl et al.; PRL 95,090404
Truscott, Baldwin et al., 2010)
32
Atoms are as fun as photons?
They can be more!
In contrast to photons, atoms can come not only as bosons (most
frequently), but also as fermions, e.g. 3He, 6Li, 40K...
Possibility to look for pure effects of quantum statistics
• No perturbation by a strong “ordinary” interaction (Coulomb
repulsion of electrons)
• Comparison of two isotopes of the same element (3He vs 4He).
33
The HB&T effect with fermions:
antibunching
Two paths to go from one initial
state to one final state: quantum
interference
Amplitudes added with opposite signs: antibunching
Two particles interference effect: quantum weirdness, lack of statistical
independence although no real interaction
… no classical interpretation
n(t )2  n(t )
2
impossible for classical densities
34
The HB&T effect with fermions:
antibunching
Two paths to go from one initial
state to one final state: quantum
interference
Amplitudes added with opposite signs: antibunching
Two particles interference effect: quantum weirdness, lack of statistical
independence although no real interaction
… no classical interpretation
n(t )2  n(t )
2
impossible for classical densities
Not to be confused with antibunching for a single particle (boson or fermion):
a single particle cannot be detected simultaneously at two places
35
Evidence of fermionic HB&T antibunching
Electrons in solids or in a beam:
M. Henny et al., (1999); W. D.
Oliver et al.(1999);
H. Kiesel et al. (2002).
Neutrons in a beam:
Iannuzi et al. (2006)
Heroic experiments, tiny signals !
36
HB&T with 3He* and 4He*
an almost ideal fermion vs boson comparison
Neutral atoms: interactions negligible
Samples of 3He* and 4He* at same temperature
(0.5 mK, sympathetic cooling) in the trap :
 same size (same trapping potential)
 Coherence volume scales as the atomic
masses (de Broglie wavelengths)
 ratio of 4 / 3 expected for the HB&T widths
Collaboration with VU Amsterdam (W Vassen et al.)
37
HB&T with 3He* and 4He*
fermion versus bosons
Jeltes et al. Nature 445, 402–405 (2007) (Institut d’Optique-VU)
4He*
Direct comparison:
• same apparatus
• same temperature
Ratio of about 4 / 3 found for
HB&T signals widths (mass ratio,
ie de Broglie wavelengths ratio)
3He*
Pure quantum statistics effect
Collaboration with VU Amsterdam (W Vassen et al.)
Fermion anticorrelation also seen in Mainz : Rom et al. Nature 444, 733–736 (2006)
38
The Hanbury Brown and Twiss effect
and other landmarks in quantum optics:
from photons to atoms
• The Hanbury Brown and Twiss photon-photon
correlation experiment: a landmark in quantum optics
• Atomic HBT with He*
• Pairs of quantum correlated atoms in spontaneous
4-wave mixing of matter waves
39
From quantum photon optics
to quantum atom optics
Photon counting (1950):
start of modern qu. optics:
Single atom detection, resolved
in time and space (2005-)
photon corr.
functions: HBT
Atom correlation functions:
atomic HBT,
No equivalent to fermions
Fermions and bosons
Correlations in atomic cascade photon
Correlations in atom pairs from
pairs (1967)
molecular dissociation (D Jin)
Entanglement, Bell in. tests (1972,1982)
No entanglement observed yet
1970: photon pairs in
non-linear crystal
1987: entanglement
easier to obtain
An equivalent in non-linear
atom optics?
Non linear mixing of matter waves
(4-wave mixing)
(3) non-linear atom optics process (NIST, MIT)
3 colliding
BEC’s
p 2  p1
p3  p1  p2
p1
p3
p2
p2
Appearance of a
daughter BEC
p3
p1
p4
p 4   p3
Amplification
of probe 3
41
(3) non-linear mixing of matter waves
(4-wave mixing)
Stimulated process : appearance of a daughter BEC
observed (NIST, MIT)
3 colliding
BEC’s
p 2  p1
p1
p3  p1  p2
p3
p2
p2
daughter BEC
p3
p1
p4
p 4   p3
Amplification
of 3
Spontaneous process: appearance of pairs
predicted (Meystre, Cirac-Zoller, Drummond, Kurisky, Moelmer…)
p3
spontaneous
p’3
2 colliding
p1
p2
p2
atom pairs
p1
BEC’s
p 4   p3
p 2  p1
p’4
p4
p4  p3  p1  p2
p1  p2
42
Observation of spontaneous
4-wave mixing in collision of two 4He* BEC’s
2 colliding
BEC’s
p 2  p1
p1
p2
p1  p2
p2
p3
p’3
p1
p4
p4  p3  p1  p2
p’4
Observation of
the full s-wave
scattering
spherical shell
p reconstruction by
elementary kinematics
(free fall)
s-wave collision
halo ( cf. MIT,
Penn state,
Amsterdam)
43
Observation of correlated 4He* pairs
p3
p1
Colliding BEC’s
p2
p4
p 2  p1
p 4   p3
p3  p 4  const
Momentum correlation in scattered
atoms
Correlation of
antipodes on
momentum sphere
Atoms in pairs of
opposite momenta
g (2) (V1  V2 )
g (2) (V1  V2  )
A. Perrin et al. PRL 2007
Are there other correlations in the momentum distribution?
44
HBT correlations in the s-wave
collision halo
HBT correlations observed for (almost) collinear atoms!
p3
p1
p2
p4
g(2)(V1  V1)
Theory far from trivial (coll. K Moelmer, K. Keruntsyan)
How can we get a chaotic statistics (HBT) from a collision between
coherent ensembles of atoms (BEC’s)?
Correlation between atoms of two different pairs: trace over the
partners yields Gaussian statistics.
Recently observed with photons
45
Summary: progress in quantum atom optics
HB&T observed with bosons and fermions
p
Observation of pairs of atoms obtained in a
p
p
spontaneous non-linear atom optics process
p
Fully quantum process:
• back to back correlations = particle image;
• HBT = 2 particle quantum amplitudes (or classical waves)
• Number difference squeezing observed (JC Jaskula, PRL 2010)
3
1
2
4
A tool for atom interferometry below the quantum standard limit
(Bouyer & Kasevich, Dunningham, Burnett, Barnett)
Summary: progress in quantum atom optics
HB&T observed with bosons and fermions
p
Observation of pairs of atoms obtained in a
p
p
spontaneous non-linear atom optics process
p
Fully quantum process:
• back to back correlations = particle image;
• HBT = 2 particle quantum amplitudes (or classical waves)
• Number difference squeezing observed (JC Jaskula, PRL 2010)
3
1
2
4
A tool for atom interferometry below the quantum standard limit
(Bouyer & Kasevich, Dunningham, Burnett, Barnett)
Do we have entangled atom pairs?
p’3
p3
p4
p’4
Simplified model, in analogy to quantum photon optics: yes!
Entanglement in momentum space:   p3 , p3  p3 , p3
To be distinguished from incoherent mixture of   p3 , p3 and p3 , p3
47
Demonstration of momentum entanglement
A possible scheme
How to show entanglement in
1
 
 p3 , p4  p3 , p4
2

?
Recombine p3 and p’3 , p4 and p’4 , and look for a modulation of
coincidence rates N++ , N+ , N+ , N , vs
a


b
p3
p’4
p’3
p4


a  b
With photons
Proposal: Horne, Shimony,
Zeilinger: PRL 1989
Expt: Rarity, Tapster, PRL 1990
48
Demonstration of momentum entanglement
A possible scheme
How to show entanglement in
1
 
 p3 , p4  p3 , p4
2

?
Recombine p3 and p’3 , p4 and p’4 , and look for a modulation of
coincidence rates N++ , N+ , N+ , N , vs
a


b
p3
p’4
p’3
p4


a  b
With photons
Proposal: Horne, Shimony,
Zeilinger: PRL 1989
Expt: Rarity, Tapster, PRL 1990
With atoms, experiments are going to be hard, but a similar scheme to test
Bell’s inequalities seems possible… hopefully before 2024!
 Might be used to test non-trivial BCS like states with cold atoms
(T. Kitagawa, M. Greiner, AA, E. Demler, PRL 2011)
49
Groupe d’Optique Atomique du
Laboratoire Charles Fabry de l’Institut d’Optique
Chris Westbrook
Philippe Bouyer
C. Westbrook
1 D BEC
ATOM LASER
Vincent Josse
David Clément
Juliette Billy
William Guérin
Chris Vo
Zhanchun Zuo
The He* team
THEORY
L. Sanchez-Palencia
A. Perrin
D. Boiron
Fermions Bosons
mixtures
Thomas Bourdel
Gaël Varoquaux
Jean-François Clément
Thierry Botter
J.-P. Brantut
Rob Nyman
BIOPHOTONICS
Karen Perronet
David Dulin
Nathalie Wesbrook
ELECTRONICS
André Villing
Pierre Lugan
M. BonneauFrédéric Moron
J.C. Jaskula
V. Krachmalnicoff
He* BEC
Denis Boiron
A. Perrin
V Krachmalnicoff
Hong Chang
Vanessa Leung
ATOM CHIP BEC
Isabelle Bouchoule
Jean-Baptiste Trebia
Carlos Garrido Alzar
OPTO-ATOMIC CHIP
Karim el Amili
Sébastien
Gleyzes
G. Partridge
50