Download Comprehensive Exam Mainul Islam Department of Computer

Comprehensive Exam
Mainul Islam
Department of Computer Science & Engineering
University of Texas at Arlington
April 20th, 2012
Supervisor: Dr. Christoph Csallner
Committee members:
Dr. David Kung
Dr. Donggang Liu
Dr. Jeff Lei
Genetic Algorithms for
Randomized Unit Testing
James H. Andrews
Tim Menzies
Felix C.H. Li
IEEE TRANSACTIONS ON SOFTWARE ENGINEERING, VOL. 37, NO. 1,
JANUARY/FEBRUARY 2011
Contribution
• Nighthawk, a novel two-level genetic random
testing system that encodes a value reuse policy.
• Optimizing the Genetic Algorithm using a
“Feature Subset Selection” tool to achieve nearly
the same (90%) coverage 10 times faster.
• The optimization learned from one set of classes
(Java utils) is successfully applied to another set
of classes (Apache system).
Genetic Algorithm (GA)
•
•
•
•
•
Chromosomes <set of parameters/gene-type>
Population <set of chromosomes>
Candidate Solutions <set of possible solutions>
Fitness Function
Genetic operator
– Mutation
– Crossover
GA Gene-types: In this research
•
•
•
•
Number of Method Calls, n
Lower bound, l
Upper bound, u
…
• Chromosome <n, l, u, …>
NightHawk
• Lower level
– Randomized Unit-testing Engine
– Constructs and Run a test case
• Upper level
– Genetic Algorithm
– Performs usual chromosome evaluation step
(fitness evaluation, mutation, crossover)
Randomized Unit-Testing (RU)
• Input: Chromosome
• M – set of Target Methods
• IM – set of all types in M (including primitive
types)
• CM – set of all callable methods in M
Each type t ε IM has an array of “value-pools”
RU: High-level view
Chromosome
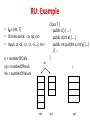
RU: Example
• IM = {int, T}
• Chromosome: <n, np, nv>
• Input: c1 <3, <2, 1>, <5, 3, 4>>
n = numberOfCalls
np = numberOfPools
Nv = numberOfValues
Class T {
public c() { … }
public c(int x) { … }
public int put(int x, int y) {…}
// …
}
int
T
vp1
vp2
vp1
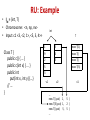
RU: Example
• IM = {int, T}
• Chromosome: <n, np, nv>
• Input: c1 <3, <2, 1>, <5, 3, 4>>
Class T {
public c() { … }
public c(int x) { … }
public int
put(int x, int y) {…}
// …
}
int
T
1
5
new T(1)
9
6
new T()
2
5
new T()
5
new T(5)
3
v1
v2
…
new T().put( 1, 5 )
new T(5).put( 1, 2 )
new T().put( 5, 5 )
…
v1
RU: ConstructRunTestCase
RU: tryRunMethod
Example: Triangle Unit Form
triangleCheck (int x, int y, int z) {
//…
if(x == y || y == z || z == x) {
if (x == y && y == z)
print “equilateral”
else
print “isoscales”
}
//…
}
Genetic Algorithm (GA)
• Performs usual chromosome evaluation step
(fitness selection, mutation, crossover)
• Input: set M of target methods
- Constructs an initial population of size, p
- Loops for desired number of generations, g
- Clone the fittest chromosome, mutating the
genes using point mutation, m
GA (continued…)
• Default Settings:
p = 20
g = 50
m = 20
• Fitness Function:
(number of coverage points covered) *
(coverage factor) - (number of method
calls performed overall)
Optimization of GA (OGA)
• Feature Subset Selection (FSS)
• RELIEF – FSS tool
– Assumes that the data are divided into groups and
tries to find the features that serve to distinguish
instances in one group from instances in other
groups.
– Calculate the merit of a feature
– Core intuition: Features that change value
between groups are more meritorious than
features that change value within the same group.
OGA: Analysis Activities
• Merit Analysis
• Gene-Type Ranking
• Progressive Gene-Type Knockout
OGA: Merit Analysis
• Finds a “merit” score between for each of the
genes corresponding to the subject unit.
• The input to the merit analysis, for a set of
subject classes, is the output of one run of
Nighthawk for 40 generations on each of the
subject classes
• Each run yields a ranked list R of all genes
– merit (g, u) is the RELIEF merit score of gene g derived
from unit u
– rank (g, u) is the rank in R of gene g derived from unit
u
OGA: Gene-Type Ranking
• bestMerit(t)
- is the maximum, over all genes g of type t and all
subject units u, of merit (g, u)
• bestRank(t)
- is the minimum, over all genes g of type t and all
subject units u, of rank (g, u)
• avgMerit(t)
- is the average, over all genes g of type t and all
subject units u, of merit (g, u)
• avgRank(t)
- is the average, over all genes g of type t and all
subject units u, of rank (g, u)
OGA: Gene-Type Ranking
OGA: Progressive Gene-Type
Knockout
• Assume a constant value for each gene of that
type
– Run NightHawk on subject unit with all 10 gene
types
– Then with the lowest (least useful) gene type
knocked out
– Then the lowest two gene types knocked out
– So on…
• Compare the results
Case Study: Initial
• 16 classes from “Collection” and “Map” (of Java
1.5.0) – 12,137 LOC
• Perform merit analysis, gene-type ranking and
progressive gene-type knockout based on
bestMerit and bestRank
• Only best four gene types according to the
bestMerit and best seven gene types according
to the bestRank ranking can achieve 90 percent
of coverage within 10 percent of time
Case Study: Reranking
Case Study: Reranking
Case Study: Optimizing numberOfCalls
Case Study: Analyzing optimized
version
CUTE:
A Concolic Unit Testing Engine for C
Koushik Sen
Darko Marinov
Gul Agha
FSE’ 05, September 5–9, 2005, Lisbon, Portugal.
Solve: 2*Y
2 * oY=X
^oXo>=Yo+ 10
o =o X
Solution: x = 30,
2, y y==115
int foo(int y) {
return (2*y);
}
void testMe(int x, int y) {
int z = foo(y);
if(z == x) {
if(x >= y+10) {
// ERROR;
}
}
}
DART
Concrete
Execution
Concrete
State
Symbolic
Execution
Symbolic
State
x = 4, y = 5
x = Xo, y = Yo
z = 10
x = 2, y = 1
z = 2 * Yo
x = Xo, y = Yo
z=2
x = 30, y = 15
z = 2 * Yo
Path
Condition
2 * Yo = Xo
z = 30
x = 4, y = 5
x = Xo, y = Yo
z = 10
z = 2 * Yo
Xo < Yo + 10
2 * Yo != Xo
Solve: (2*Y
10= X
Xo
o)%50=
o
Stuck? Yox with
Solution:
Replace
= 10,5y = 5
int foo(int y) {
return (2*y)%50;
}
void testMe(int x, int y) {
int z = foo(y);
if(z == x) {
if(x >= y+10) {
// ERROR;
}
}
}
DART
Concrete
Execution
Concrete
State
x = 4, y = 5
z = 10
Symbolic
Execution
Symbolic
State
Path
Condition
x = Xo, y = Yo
z= (2*Yo)%50
x = 4, y = 5
x = Xo, y = Yo
z = 10
z=(2*Yo)%50
(2*Yo )%50!=Xo
CUTE
• Deals with Pointer
• Represents inputs using a logical input map
• It is sufficient to know how the memory cells
are connected
CUTE: WorkFlow
• Uses the logical input map to generate a concrete input
memory graph for the program and two symbolic states,
– One for pointer values
– One for primitive values
• Runs the code on the concrete input graph, collects
constraints that characterize the set of inputs that would
take the same execution path as the current execution
path.
• It negates one of the collected constraints and solves the
resulting constraint system to obtain a new logical input
map.
CUTE: Example
XO > 0
PO != NULL
2 * XO +1 == VO
PO == NO
Optimizing Constraint Solving
• Fast Unsatisfiability Check
• Common Sub-constraints Elimination
• Incremental Solving
Data Structure Testing
• Generating Inputs with Call Sequences
• Solving Data Structure Invariants
Experiments
Differential Symbolic Execution
Suzette Person
Matthew B. Dwyer
Sebastian Elbaum
Corina S. Pasareanu
FSE-16, November 9–15, Atlanta, Georgia, USA.
Introduction
• Existing techniques for characterizing code changes are
imprecise leading to unnecessary maintenance efforts.
• Differential symbolic execution (DSE), exploits the fact
that program versions are largely similar to reduce cost
and improve the quality of analysis results.
• For example, during regression testing, differences can
be used to focus re-testing efforts by selecting only test
cases that exercise the modified code.
Contribution
• Precisely characterizing behavioral program
differences.
• Compute over-approximating symbolic method
summaries by identifying and automatically
summarizing the behavior of common program
fragments.
• Defines two behavioral equivalences between
program versions.
Contribution (continued…)
• Techniques for post-processing symbolic
execution results to compute behavioral
differences.
• Defines the conditions under which DSE analysis
results completely account for program behavior
and, importantly when they do not.
• Describes three applications of DSE results to
support the automation of program evolution
tasks.
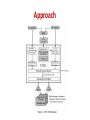
Approach
Summarizing Program Behavior
• Symbolic summary
y=x;
If( y > 0 ) then y++;
return y;
• Symbolic Execution calculate two behaviors:
( X > 0 , y=x ^ RETURN == X+1 )
( !(X > 0) , y=x ^ RETURN == X )
Symbolic
summary
Example: Refactoring
final int THRESHOLD = 100;
public int logicValue(int t) {
int elapsed = currentTime – t;
int val = 0;
if(elapsed < THRESHOLD) {
val = old;
} else {
public int logicValue(int t) {
if(!(currentTime – t >= 100)) {
return old;
} else {
int val = 0;
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
C
return val;
return val;
}
}
}
}
Version 1
Version 2
Example: Behavioral Change
final int THRESHOLD = 100;
public int logicValue(int t) {
int elapsed = currentTime – t;
int val = 0;
if(elapsed < THRESHOLD) {
val = old;
} else {
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
final int THRESHOLD = 100;
public int logicValue(int t) {
int elapsed = currentTime – t;
int val = 0;
if(elapsed < THRESHOLD) {
val = 1;
} else {
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
C
return val;
return val;
}
}
}
}
Version 2
Version 3
Example: Symbolic Summary for V1
public int logicValue(int t) {
if(!(currentTime – t >= 100)) {
return old;
} else {
int val = 0;
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
return val;
}
}
Version 1
- ( !(CT − T >= 100), RETURN == O )
- ((CT − T >= 100) ^ (D == null), RETURN == NRE )
- ((CT − T >= 100)^(!D== null)^!(0 < D.L),
old == 0 ^ RETURN == 0 )
- ((CT − T >= 100)^!(D== null) ^ 0 < D.L^!(1 < D.L),
old == D[0] ^ RETURN == D[0] )
- ((CT − T >= 100)^!(D== null) ^ 0 < D.L^ 1 < D.L
^ !(2 < D.L),
old == D[0] + D[1] ^ RETURN == D[0] + D[1])
Ex: Abstract Summary for C
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
for (int i=0; i<data.length; i++) {
val = val + data[i];
}
old = val;
C
• ( IPC(D, V), old = oldC(D, V) ^ val = valC(D, V) )
D, V = Symbolic Variables for data and val
IPC = Path conditions inside block C
xC(D, V) = resultant values for variable x inside
block C
Example: Method Summary for v1, v2, v3
• For Version 1:
– ( !(CT − T >= 100), RETURN = O )
– ( (CT − T >= 100) ^ IPC(D, V),
old = oldC(D, V ) ^ RETURN = valC(D, V) )
• For Version 2:
– ( CT − T < 100), RETURN = O )
– ( !(CT − T < 100) ^ IPC(D, V ),
old = oldC(D, V ) ^ RETURN = valC(D, V) )
• For Version 3:
– ( CT − T < 100), RETURN = 1 )
– ( !(CT − T < 100) ^ IPC(D, V),
old = oldC(D, V ) ^ RETURN = valC(D, V) )
Example: Delta, Δ
• V1 and v2 are equivalent
• Δv3, v2 = { (CT − T < 100), RETURN = 1) }
• Δv2, v3 = { (CT − T < 100), RETURN = O) }
On Input
Version 2
Version 3
currentTime – t < 100
returns old
returns 1
Equivalence
• Functional Equivalence
– Ignore internal details of a method
– “what” effects it computes for a given input
• Partition-effects Equivalence
– Considers both: “what” a method does and
– “how” it partitions the input space
Equivalence and Delta
• Functional Equivalence and Delta
– Ignore internal details of a method
– “what” effects it computes for a given input
• Partition-effects Equivalence and Delta
– Considers both: “what” a method does and
“how” it partitions the input space
Application
• Refactoring Assurance
• Characterize changes
• Test Suite Evolution
Experiments
• SIENA
–
–
–
–
6 KLOC and 26 Classes
28 methods were changed in first 5 versions
7 involved actual code change
Out of 7, 3 were summarized completely using SE and
other 2 were summarized with DSE
• ApacheJMeter
–
–
–
–
43 KLOC and 389 Classes
352 methods were changed between version 1 and 2
95 involved functional code change
68 methods were summarized completely using DSE
Strength
• Precise characterization
• Potential to reduce the cost of Software
Maintenance activities
Limitation
• Do not address the problem if changes occur
in places where symbolic execution is not
bounded, such as loop.
• Summaries cannot be computed for methods
whose behavior is defined in external libraries.
• This approach is not integrated with reuse of
existing test cases.
Dynamic Test Input Generation for
Database Applications
Michael Emmi
Rupak Majumdar
Koushik Sen
ISSTA’07, July 9.12, 2007, London, England, United Kingdom.
Goal
• Test Database Application
• Achieve Higher coverage by generating:
– Inputs
– Database States
Contribution
• An algorithm that generates both program inputs
and database states.
• A constraint solver that can solve symbolic
constraints consisting of both linear arithmetic
constraints over variables as well as string
constraints (string equality, dis-equality).
• Evaluation of the algorithm on a Java
implementation of MediaWiki, a popular wiki
package.
WorkFlow
• Concolic Execution
• Collect program constraints and database
constraints
• Solve the constraints
• Update Database
Example
Program Input
Query
Goal 1
Goal 2
Example
v.inventory > 0 ^ v.subject LIKE ‘CS%’
isbn 1
publisher ‘ABS@E’
inventory 101
subject ‘CS’
Results.get(“Publisher”) != ACM
isbn 776 publisher ‘ACM’
inventory 122
subject ‘CS’
Experiments
• Implementation: on top of JCute
• MediaWiki Package
• 75% of branches covered where Jcute alone
Covered 50% branches
Questions?