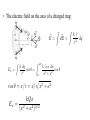* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download CH21-electric force and fields
Introduction to gauge theory wikipedia , lookup
Weightlessness wikipedia , lookup
Anti-gravity wikipedia , lookup
Circular dichroism wikipedia , lookup
Speed of gravity wikipedia , lookup
Magnetic monopole wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Fundamental interaction wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Electromagnetism wikipedia , lookup
Maxwell's equations wikipedia , lookup
Field (physics) wikipedia , lookup
Lorentz force wikipedia , lookup
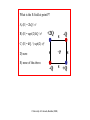
Chapter 21: Electric Charges and Forces Electric Force The electric force is one of the fundamental forces of nature. Often rubbing two objects together causes them to experience an electric force. Examples: •Unrolling plastic rap •Running a comb through hair •Rubbing rubber/plastic/glass rods with fur and silk •Walking on carpet with slippers • Consider the following experiments to help determine the nature and cause of this force: The Charge Model 4 • Frictional forces add or remove something called charge to/from an object. More vigorous rubbing produces a larger quantity of charge. • There are two kinds of electric charge: positive and negative (arbitrary names). • Choice of what is a positive charge and a negative charge is arbitrary (glass being rubbed with silk is defined as positive charging). • Charged particles exert an electric force on other charged particles. • Objects with like charges repel. • Objects with opposite charge attract. The Charge Model Cont’d • A 3rd type of charge that is attracted to both positive and negative charges has never been found. • Neutral macroscopic objects have an equal mixture of positive and negative charge. • The electric force is a long-range force, but decreases with increasing distance. Clicker Question From the picture, what can you conclude about the three charges? 1) 2) 3) 4) Purple and yellow have opposite charges Purple and yellow are both positive. Purple, yellow, and green are all positive. Purple, yellow, and green are either all positive or all negative, but there is no way to determine which. Conductors and Insulators • Conductors are materials where charge is free to move. All metals are conductors. • Insulators are materials where charge isn’t free to move. Examples include wood, plastic, & glass. Modern picture Clicker Question An electroscope consists of a neutral conducting sphere connected to metal leaves via a metal rod. Why do the leaves of the electroscope repel each other when the positively-charged rod is brought near the sphere? 1. The leaves become negatively charged 2. The leaves become positively charged 3. The leaves are neutral, but are attracted to the charged rod Clicker question A negatively charged glass rod is brought near a spherical conductor, which is initially neutral. The spherical conductor is initially touching another spherical conductor which is also initially neutral. While the glass rod is near the conductor, the two conductors are separated (and kept separated). The glass rod is then removed. What are the charged states of the two conductors? 1. Left is positively charged, right is negatively charged. 2. Left is negatively charged, right is positively charged. 3. Left is positively charged, right is neutral. Experiments with neutral object Consider a couple experiments involving a macroscopic neutral object: How can a charged object attract a neutral, macroscopic object? Coulomb’s law (the Electric force) • The magnitude of the electric force between two point-like particles depends on: • The product of the two charges • The inverse square of the distance between them • Coulomb’s law: F~12 kq1 q2 = r̂ r2 r Here F F~12 12 is the force q1 exerts on q2 and rˆ is a unit vector pointing from q1 toward q2 . k is the Coulomb constant , 9 2 2 approximately 9.0 ´ 10 N × m / C . Clicker question 16 Determine the charge of the spheres in terms of mass m, distance d, g, and θ. The superposition principle • The electric force obeys the superposition principle. • That means the force two charges exert on a third force is just the vector sum of the forces from the two charges, each treated without regard to the other charge. • The superposition principle makes it mathematically straightforward to calculate the electric forces exerted by distributions of electric charge. • The net electric force is the sum of the individual forces. Clicker Question CT 25.11 Consider the charge configuration shown below. What is the direction of the net force on the +q charge? B +q A C h E s/2 s/2 +Q -Q ©University of Colorado, Boulder (2008) D Example: Two positive charges of charge q are a distance 2a apart. A third charge of charge Q is a distance y above the midpoint of the other two charges. What is the net force on Q? y +Q y q x=−a q x=a x Fy = 2kqQ/r2 (y/r) 2kqQy F = 2 (a + y 2 )3/2 F y/a The Electric Field, E • The electric field at a point in space (due to a distribution of charges) is the force per unit charge that a test-charge q’ (at that point) would experience: ~ F ~ = E q0 The electric field exists in space (even if no charge exists there). phet simulation General Principles phet field of dreams Slide 26-108 QuickCheck 26.12 Which electric field is responsible for the proton’s trajectory? A. B. C. D. E. Slide 26-84 Fields of point charges and charge distributions • Based on Coulomb’s law, the field of a point charge is radial, outward for a positive charge and inward for a negative charge. kq ~ = E r̂ r2 Superposition • The superposition principle states that, for a collection of charges, the total electric field at a point is simply the summation of the individual fields due to each charge ~ = E X i ~i = E X kqi i ri2 r̂i Clicker Question CT 26.7 What is the E-field at point P? A) |E| = 2kQ / s2 B) |E| = sqrt(2) kQ / s2 +2Q s -Q C) |E| = kQ / ( sqrt(2) s)2 s D) zero E) none of the above. -Q ©University of Colorado, Boulder (2008) P s s +Q QuickCheck 26.5 What is the direction of the electric field at the blue point in the figure (directly to the right of the center of the dipole)? E. The field is zero. http://phet.colorado.edu/sims/charges-and-fields/charges-and-fields_en.html Slide 26-41 The Dipole Electric Field at Two Points Slide 26-32 The Dipole Electric Field at Two Points Above dipole: Ey = kq/(y S/2)2 kq/(y + S/2)2 1 1 1 1 = 2 ⇡ 2 (1 ⌥ 2(S/2y)) 2 2 (y ± S/2) y [1 ± S/(2y)] y kq 2S 2kqS ) Ey ⇡ 2 ⇤ = y y y3 Slide 26-32 Continuous Charge Distribution • Macroscopic objects typically contain so many excess protons or electrons (say, over 1012), it is a very good approximation to describe the distribution to be continuous. • Instead of summing over every single point charge, we integrate over the infinitesimal spatial chunks of charge. Superposition E field at P due to Δq ~ =k E q r2 ~ = E r̂ X ~ E In limit that volume becomes infinitesimally small: q ! dq ~ = E Z dq ~ ~ E ! dE = k 2 r̂ r ~ = dE Z k r̂ dq 2 r Z Z k r̂ dq 2 r • What is dq in terms of charge density? ~ = E ~ = dE 1D 2D 3D dq=σdA dq=λdx dx dq = dl ~ = E Z k dl r̂ r2 dq = da ~ = E Z k da r̂ r2 dq = ⇢dV ~ = E Z k⇢ dV r̂ r2 Note that, in general, r̂ changes direction during the integral! Do integral one component at a time. Example: Line Charge Let’s calculate the electric field a distance a to the right of the right end of a uniform line charge of length L and charge Q. Q Z Z ++++++++++ L k r̂ dq = 2 r ~ = E a Since charge distribution is uniform: = k dl r̂ r2 Q L Pick a coordinate system: say the x-axis along the rod with origin at point where we are evaluating the E-field. Ex = Z a (L+a) k dx x2 = k | x kQ = a(L + a) kQ Ex ! 2 a a (L+a) Note: as a becomes much bigger than L, Example: Line Charge (alternate origin) Let’s repeat problem but now put origin on left end of rod: Q ++++++++++ L a Since charge distribution is uniform: ~ = E = Z k r̂ dq = 2 r Z k dl r̂ r2 Q L Pick a coordinate system: say the x-axis along the rod with origin at point where we are evaluating the E-field. Z L k k k k L Ex = dx = |0 = 2 x) a+L x a L+a 0 (a + L k L kQ Ex = = a(L + a) a(L + a) Clicker Question • If the line charge collapsed to a point charge, situated where the middle of the line charge was, the electric field (at the dot) would 1. increase 2. decrease 3. remain the same Q ++++++++++ L a E=? Q E=? a + L/2 QuickCheck 26.8 Uniform rod with charge Q. In which direction is the electric field at point a distance y above rod? Slide 26-52 QuickCheck 26.8 Clicker Question At the dot (a distance y from origin), the y-component of the electric field due to the shaded region of charge is dEy = ? A. B. C. D. E. [k = 1/(4⇡✏0 )] Slide 26-52 Ey = Z L/2 L/2 1 y dx 2 yx L/2 p = |0 2 2 3/2 4⇡✏0 (x + y ) 4⇡✏0 y 2 x2 + y 2 1 2 1 p Ey = 4⇡✏0 y 1 + 4y 2 /L2 For an infinitely-long rod: 2k Ey = y Figure 21.49 The electric field at point P is 1. 2. 3. 4. kQ/a2 less than kQ/a2 but greater than zero zero Depends on the value of the charge at point P • The electric field on the axis of a charged ring: ~ = E Ex = Z k dq cos ✓ = 2 r cos ✓ = x/r = x/ Z 2⇡ 0 p ~ = dE k ad cos ✓ 2 2 x +a x2 + a2 kQx Ex = 2 (x + a2 )3/2 Z Z k r̂ dq 2 r • The electric field on the axis of a charged ring: • Notice that since all chunks of charge contribute equally, there really isn’t a need to integrate spatially: Z k dq k Qx Ex = cos ✓ = 2 2 r r r kQx Ex = 2 (x + a2 )3/2 A Ring of Charge § The electric field on the x-axis points away from the center of the ring, increasing in strength until reaching a maximum when |z| ≈ R, then decreasing: x Ex = kQ 2 (x + R2 )3/2 Slide 26-55 • Electric field due to disk of radius R and charge Q (a distance x from center): E= E= Z Z dERing = R 0 Z k dQRing x (x2 + r2 )3/2 k 2⇡r dr x (x2 + r2 )3/2 1 R E = 2⇡ kx 2 | (x + r2 )1/2 0 ✓ E = 2⇡ k 1 x p x2 + R 2 ◆ Field lines • Field lines show the direction of the electric field. The density of field lines is proportional the the strength of the field. • Examples: This figure represents the electric field of a dipole as a field-vector diagram. This figure represents the electric field of a dipole using electric field lines. phet: charges The dipole: an important charge distribution • An electric dipole consists of two point charges of equal magnitude but opposite signs, held a short distance apart. • The dipole is electrically neutral, but the separation of its charges results in an electric field. • Many charge distributions, especially molecules, behave like electric dipoles. • The product of the charge and separation is the dipole moment: p = qs. • Far from the dipole, its electric field falls off as the inverse cube of the distance. 3 (E / 1/r ) Clicker Question 1. 2. 3. 4. 5. (a) only (c) only (a) and (b) (c) and (d) (a), (b), (c) and (d) Dipoles in a Uniform Electric Field Dipoles in a Uniform Electric Field § The figure shows an electric dipole placed in a uniform external electric field. § The net force on the dipole is zero. § The electric field exerts a torque on the dipole which causes it to rotate. Slide 26-86 The Torque on a Dipole ~⌧ = ~r ⇥ F~ The torque on a dipole placed in a uniform external electric field is ✓ ◆ ⌧ =2 1 s sin ✓ 2 (qE) = pE sin ✓ Slide 26-93 Dipoles in a Non-uniform Electric Field Field § Suppose that a dipole is placed in a non-uniform electric field, such as the field of a positive point charge. § The first response of the dipole is to rotate until it is aligned with the field. § Once the dipole is aligned, the leftward attractive force on its negative end is slightly stronger than the rightward repulsive force on its positive end. § This causes a net attractive force. Slide 26-99