Download electric field - Experimental Elementary Particle Physics Group

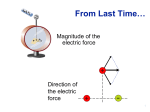
The Electric Field
We know that the electric force between charges is transmitted by force
carriers, known as “photons”, more technically known as “virtual
photons” since they are not freely traveling through space.
But even single, isolated charged particles are surrounded by clouds of
virtual photons. A charged particle is said to have an “electric field”
extending into space in all directions. The presence of this field can be
tested by bringing another charged particle nearby (a “test charge”), to
see if a force appears along the line between their centers (see
Coulomb’s Law).
How is the electric field defined mathematically? It is the electric force per
unit charge. If we think of a test charge q0 as a “field measuring
device”, and place it at some position r where there is a field, then:
Electric field

 F
E
q0
Force on the test charge
Magnitude of test charge
N 
 C 
Note: The electric field is there, even when the test charge is not!
Units
Electric field of a single charge, Q
If we bring a test charge to some distance r from a single charge Q, we can
solve for the electric field at that position using Coulomb’s Law:

 F  F   kQq0  1 
kQ
E    rˆ   2  rˆ  2 rˆ
q0  q0   r  q0 
r
Electric field of a single charge Q
If we carry the test charge to many locations to map out the electric field,
we will get the following picture:
The “other” electric constant,  0
Before we go any further, you should be aware that there is another
constant, 0 (the “permittivity of free space”), that we can use as an
alternate to k in our expressions for electric force or electric field (or
anywhere else it appears). This new constant will be handy in some
problems involving electric fields, but often it clutters up expressions
because of extra constants appearing with it.
Voila!
1
k
 8.99  10 9 Nm 2 / C 2 ,  0  8.85  10 12 C 2 / (Nm 2 )
40
For example, Coulomb’s Law and the electric field of a single charge would
appear as:
 Q1Q2
F
rˆ
2
40 r

E
Q
40 r
2
rˆ
Formidable!
Electric field lines of a point charge, Q
There is an alternate, “easier to read”, method for graphing electric fields.
Instead of graphing individual E field vectors at a selection of locations, we
connect the vectors of the field into continuous lines, called “field lines”.
+
In this representation, the lines show
only the direction of E. Field lines start
on positive charges and end on
negative charges.
The line length no longer represents the
field magnitude. Now, the field is
stronger where the lines are more
densely packed!
Like electric force vectors, electric field vectors from
different charges add. (Superposition principle.)
+
+
q2
q1
r2
r1
r3
+
q3
Q
E


kqi
E   Ei   2 rˆi
i
i ri
Electric dipole field
y
Dipole charges are
equal and opposite,
and equal distances
from the x axis.
r+
E
+Q
rx
-Q
 Sketch electric field.
Electric field for symmetric charge pairs
(dipole)
Continuous charge distributions
Up to this point we have been analyzing electric forces and fields
produced by one or more point charges. Now we turn to the problem
of charge distributions that have so many elementary charges in a
given region that they may be considered smooth, or “continuous”.
Line charge
dq
Surface charge
Q,L
dq
dq
ds
Q,A
dA
dq

ds
Volume charge
Q,V
dV
dq

dA
dq

dV
Calculating E for continuous charge distributions
As implied by the infinitesimals such as dq, to calculate the electric
field (seen at point “P ”) due to continuous charge distributions, we
must be prepared to integrate over all the charge in the problem.
Line charge
dq

P
ds
dq
r
ds


E P  k  ds 2 rˆ
r
Surface charge

dq
dq
dA
P
r
dA


E P  k  dA 2 rˆ
r
Volume charge

dq
dq
dV
P
r
dV


E P  k  dV 2 rˆ
r
We are using superposition here in integral form, “adding” the contributions
to E from each dq. In general, these vector integrals will be hard to do.
Ring of uniformly distributed charge
We are restricting this calculation to
the x axis. This allows us to use
symmetry to greatly simplify the
calculation.
Since Q is uniform around the ring:  
 Solve for E by integration.
dq Q
Q
 
ds C 2a
Ring of charge: sketch and graph of E along x axis
x
 Sketch full field. Also find
expressions for field in the limits
of small x and large x.
Disk of uniformly distributed surface charge
We will again find the electric field along the x
axis, using the results from the ring-charge
calculation. This time we must integrate over r.
Use integral tables in appendix at back of book.
Since Q is a uniform
surface charge:
 Solve for E by
integration. Also, sketch.
Find E in the limits of
small x and large x.

dq Q
Q
  2
dA A R
Binomial expansion needed for large x limit
n(n  1) x 2 n(n  1)( n  2) x 3
(1  x)  1  nx 

 ... ( x 2  1)
2!
3!
 1  nx
(simplest, first order approximat ion)
n
Infinite plane of uniformly distributed surface charge
We have the answer for this already! What is it?
Two planes of opposite charge: “parallel plate capacitor”
Superposition principle at work!
 Sketch the E field everywhere. Take the large d and small d
limits “graphically”. What is the result for infinite planes?
Line of uniformly distributed charge
We will find the electric field along the
x axis (at mid-line) by integrating dE
caused by the line charge elements
dQ along the y axis. Again, symmetry
makes this calculation “easier”.
dQ Q Q
Since Q is a uniform


 
line charge:
dy L 2a
 Solve for E at mid-line by integration, and
sketch full field. Also, find expressions for
field in the limits of small x and large x.
Summary: E fields for various charge distributions
Ex 
Ring
charge
small x

dq Q
Q
  2
dA A R
kQx  1  Qx
 3
 
3
a
 40  a
large x
 
2kQ 
1


Ex  2 1 
2
R 
1  R / x   2 0

Disk
charge
small x

Ex 
 1 
kQx
kQx
Qx




3/ 2
 4  2
2) 3 / 2
r3
( x 2  a 2)
0  (x  a

dQ Q Q
 
dy L 2a
Ex 
2kQ 

R2
2 0
Ex 
Line
charge
small x
Ex 
large x
Ex 
kQ  1  Q


x 2  40  x 2


1
1 

2

1  R / x  
Ex 
kQ  1  Q


x 2  40  x 2
 1 
Q

 
x x 2  a 2  40  x x 2  a 2
kQ
2k


x
2 0 x
Notice dependence on r when symmetry is 1D, 2D, or 3D.
large x
Ex 
kQ  1  Q


x 2  40  x 2
Charged particles motion in an electric field
A positive charged particle in an
electric field, E, will feel a force, F,
in the direction of the field.
F = qE
In a uniform electric field, the
particle trajectories will, in
general, be parabolic. Where
else do we see this shape of
trajectory? “Why?” What motion
occurs if we release the particle
from rest in this field?
Electrons or protons in this picture?
Electric dipoles in a uniform electric field
A system that has equal and
opposite electric charges at a fixed
distance, d, from each other is called
a “dipole”.
(Discuss H2O.)
An electric dipole in a uniform
electric field, E, will feel a torque,
t, perpendicular to E. But it feels
no net force! Why?
The torque will try to align the
dipole as shown. This this
equilibrium stable or unstable?
What about the opposite
orientation?
Electric dipole definition, and behavior in
a uniform electric field
The “dipole moment”
(not momentum)
Torque:
vector
product,
and
magnitude
 
t  pE

t  pE sin(  )
Potential energy:
dot product and
magnitude
 Derivations


p  qd
 
U  pE
U   pE cos( )
Dipoles aligned in a
non-uniform electric
field experience a
net force. Why?
What direction?
Continuous charge distributions