Download Solution of the Radial Schrödinger Equation for

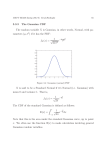
Solution of the Radial Schrödinger
Equation for Gaussian Potential
A. Hacisalihoglu*,a, Y. Kucuk b,
a
Department of Physics, Recep Tayyip Erdogan University, 53100 Rize, Turkey
b Department of Physics, Akdeniz University, 07100 Antalya, Turkey
CONTENTS
I.
Introduction
II. Asymptotic Iteration Method
III. Solution of the Radial Schrödinger Equation for
Gaussian Potential
IV. Conclusions
I. INTRODUCTION
Over the last decades, the energy eigenvalues and
corresponding eigenfunctions between interaction systems
have raised a great deal of interest in the relativistic as well as
in the non-relativistic quantum mechanics.
The exact solution of the wave equations (relativistic or nonrelativistic) are very important since the wave function contains
all the necessary information regarding the quantum system
under consideration.The Gaussian potential has been
extensively used to describe the bound and the continuum
states of the interactions systems
In general,the approximation methods have been used for the
solution of the Gaussian potential such as the;




Wentzel Kramers Brillouin Approximation [4],
Perturbation and Variational Methods [5] ,
The Higher-Order Perturbation Theory combined with Hypervirial
Pade Scheme [6],
Large-N Expansion Method [7].
In this study, we apply the asymptotic iteration method (AIM)
to solve the radial Schrödinger equation for the Gaussian potentail
without any approximation to the potential. It has been shown that
this method is very efficient to solve the Schrödinger equation for
different potentials.
This study, Investigation of the exotic nuclei reactions by using
the Continuum Discretized Coupled Channels (CDCC) Model
(project number: 110T388) from the scope of the project work was
carried out to contribute to the structure of nuclear.
At Nuclear structure process, Bohr Hamiltonian defined
excitation energy levels of nuclei was aimed to be solved by using
the method of asymptotic iteration potential for gauss potential.
II. THE ASYMPTOTIC ITERATION METHOD
AIM is proposed to solve the second-order differential
equations of the form.
y ''  0 ( x) y '  s0 ( x) y
(2.1)
where 0 ( x)  0 The variables, 0 ( x) and s0 ( x) are sufficiently
differentiable. The differential Eq.(2.1) has a general
solution.
y ( x)  e
x

 a ( x ') dx ' 







x
( 0 ( x '')

''
'' 
c c e

2
a
(
x
)
dx
 2 1 
 (2.2)


x'
If k > 0, for sufficiently large k, we obtain the  ( x ) values from
sk ( x)
skk ( x) 
  ( x)
k ( x)
(2.3)
Where k ( x) and sk ( x)
k ( x)  k 1' ( x)  sk 1 ( x)  0 ( x)k 1 ( x)
Sk ( x)  Sk 1' ( x)  S0 ( x)k 1 ( x)
k  1,2,3...
(2.4)
(2.5)
The energy eigenvalues are obtained from the quantization
condition . The quantization condition of the method together
with Eq. (2.5) can also be written as follows
(2.6)
 k ( x)  k ( x)Sk 1 ( x)  k 1 ( x)Sk ( x)  0
For a given potential such as the Gaussian potential one,
the radial Schrödinger equation is converted to the form of Eq.
(2.1). Then, 0 ( x) and s0 ( x) are determined and k ( x) and sk ( x)
parameters are calculated.
The energy eigenvalues are determined by the quantization
condition given by Eq. (2.6). In this equation, k shows the
iteration number.
For the exactly solvable potentials, the energy eigenvalues
are obtained from this equation if the problem is exactly
solvable and the radial quantum number n is equal to the
iteration number k for this case.
For nontrivial potentials that have no exact solutions, for a
specific n radial quantum number, we choose a suitable
r0 point, determined generally as the maximum value of the
asymptotic wave function or the minimum value of the
potential. The approximate energy eigenvalues are obtained
from the roots of this equation for sufficiently great values of k
with iteration.
III. THE ENERGY EIGENVALUES FOR THE GAUSSIAN
POTENTIAL
The radial Schrödinger equation is given by
d 2 Rnl (r ) 2m
 2  E  Veff (r )  Rnl (r )  0
2
dr
(3.1)
where m is the mass and Veff (r) is effective potential
l (l  1)
which is the sum of centrifugal V
and the
(r ) 
2mr
attractive radial Gaussian potentials.
2
centrifugal
Vgauss (r )   Ae
(  r 2 )
2
(3.2)
Veff (r) is effective potential which is the sum of
centrifugal and the attractive radial Gaussian potential:
(  r ) l (l  1)
Veffective (r )   Ae

2mr 2
2
2
(3.3)
where A is the depth of the Gaussian potential.
Inserting Eq. (2.7) into Eq. (2.6) and using the following
ansatzs

2mEn
2
ˆA  2mA
2
We can easily obtain

d 2 Rnl (r ) 
l (l  1) 
 r 2
    Ae

 Rnl (r )  0
2
2
dr
r


(3.4)
In order to solve this equation with AIM, we should
transform this equation into the form of Eq. (2.1).
2
It is clear that when r goes to zero, Rnl (r )  r l 1 and Rnl (r )  exp( r )
at infinity, therefore we can write the physical wavefunction
as follows
l 1   r 2
Rnl (r )  r e
f nl (r )
(3.5)
If we insert this wave function into Eq. (3.4), we have the
second-order homogeneous linear differential equations in
the following form:
d 2 f nl (r )  (l  1)
Ar 4
 df nl (r ) 
2
2 2
 2
 2r  
  2 A  2  Ar 
 6 r  4l   4r   f nl (r )
2
dr
4
 r
 dr


(3.6)
By comparing this equation with Eq. (2.1), we can easily
write the 0 (r ) and s0 (r ) values:
 (l  1)

0 (r )  2 
 2r  
 r

(3.7)
ˆ 4
 ˆ

Ar
2
2 2
ˆ
s0 (r )   2 A  2  Ar   6 r  4l   4r  
4


(3.8)
Using 0 (r ) and
values as follows:
s0 (r ) values we calculate
2
1 (r )    4r 
r
4


Ar
2
s1 (r )   2 A  Ar 2 

2(



(

3

2
r
 ))

4 

k (r )
and sk (r )
(3.9)
(3.10)
It is important to point out that if this equation can be
solved at every r point, then the problem is called as the
exactly solvable.
In our potential, since the problem is not exactly
solvable, we have to choose a suitable r0 point and solve
the equation  k (r0 ,  )  0 to find  values.
In this study, we determine the r0 value from the
maximum point of the asymptotic wavefunction, which is
the same as the root of 0 (r )  0 , namely, r  1  l
0
2
Here,  is convergence constant which affects the speed of
the convergence [19–21]. We have noticed that the
optimum value of  is problem dependent. Therefore, we
have conducted a series of calculations for  from 1 to 40
and observed that the best convergence is obtained when
the constant   10 value, which gives the energy eigenvalues
around k = 130 iterations. For other values of and high
number of quantum states, the convergence needs more
iteration to obtain the energy eigenvalues.
Şekil-1:  1 ,m=0.5, A=400,   1 , β = 10 and for l=0,1,2,3,4,5,6,7 values changes rdependent of Veff (r ) potential.
V. CONCLUSIONS
In this study, we have presented the iterative
solutions of the radial Schrödinger equation for the
attractive radial Gaussian potentials for any n and l
quantum states by using the asymptotic iteration method.
We have obtained the bound state energy
eigenvalues for any n and l states using AIM iteration
procedure without any approximation.
The obtained results of AIM calculations have been
compared the results of other studies. As shown in Table
I the very agreement between AIM calculations and other
calculations has been obtained.
The advantage of the asymptotic iteration method is
that it gives the eigenvalues directly by transforming the
second-order differential equation into a form of
f n (r )''  0 (r ) f n (r )'  s0 (r ) f n (r )
The asymptotic iteration method results in exact
analytical solutions if there is and provides the closed-forms
for the energy eigenvalues. Where there is no such a solution,
The energy eigenvalues are obtained by using an
iterative approach [12, 14, 19–21]. As it is presented, AIM
puts no constraint on the potential parameter values involved
and it is easy to implement. The results are sufficiently
accurate for the practical purposes. It is worth extending this
method to examine other interacting systems.
REFERENCES
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Aygun, M., Bayrak O. and Boztosun I. 2007. Solution of the radial Schrödinger equation for the potential family v
(r) = A/r2 - B/r + Cr2 using the asymptotic iteration method.Journal of Physics B: Atomic, Molecular and Optical
Physics 40(3): 537-544.
Barakat, T. 2006. The asymptotic iteration method for the eigenenergies of the Schrödinger equation with the
potential V(r) ≤ -Z/r + gr + λr2. Journal of Physics A: Mathematical and General 39(4): 823-831.
Bayrak, O. and Boztosun I. 2006. Arbitrary ℓ-state solutions of the rotating Morse potential by the asymptotic
iteration method. Journal of Physics A: Mathematical and General 39(22): 6955-6963.
Bayrak, O. and Boztosun I. 2007. An alternative accurate solution of the exponential cosine screened Coulomb
potential. International Journal of Modern Physics C 18(9): 1443-1451.
Bayrak, O. and Boztosun I. 2007. Bound state solutions of the Hulthén potential by using the asymptotic iteration
method. Physica Scripta 76(1): 92-96.
Bessis, N., G. Bessis and Joulakian B. 1982. A note on the Schrödinger equation for the potential A exp(-x 2 )l(l+1)/x 2. Journal of Physics A: Mathematical and General 15(12): 3679.
Buck, B, Friedrich H. and Wheatley C. 1977. "Local potential models for the scattering of complex nuclei." Nuclear
Physics A 275(1): 246-268.
Ciftci,H., Hall R. L. and Saad N. 2003. Asymptotic iteration method for eigenvalue problems, . Journal of Physics
A: Mathematical and General 36
Ciftci, H., Hall R. L. and Saad N. 2005. Construction of exact solutions to the eigenvalue problems by the
asymptotic iteration method. Journal of Physics A: Mathematical and General 38(5): 1147-1155
Fishbane P. M., Gasiorowicz S. , Thornton T.2007. Temel Fizik Cilt II. Arkadaş Yayınları, Ankara.
Griffiths J.( Çev: Özbek H),1999. Kuantum Mekaniğine Giriş Nobel Yayın Dağıtım, Ankara.
12.
13.
14.
15.
16.
17.
18.
Gündüz E. 1999. Modern Fiziğe Giriş. Ege Üniversitesi Yayınlar, İzmir.
Hirschfelder J O 1960 Classical and quantum mechanical hypervirial theorems J. Chem. Phys. 33 1462–6
Karaoğlu B. 1998. Kuantum Mekaniğine Giriş. Güven Yayıncılık, Ankara
Kocak, G., Bayrak O. and Boztosun I. 2007. Arbitrary ℓ-state solution of the Hellmann potential. Journal of
Theoretical and Computational Chemistry 6(4): 893-903.
Krane KS. (Çev: B. Şarer), 2001. Nükleer Fizik 1. ve 2. Cilt. Palme Yayıncılık, Ankara.
Lai C S. 1983. On the Schrödinger equation fort he gaussian potential . J. Phys. A: Math. Gen. 16:L181-L185
Li Y., Zhang F and Chen J. 2011. Virial theorem and hypervirial theorem in a spherical geometry. J. Phys. A: Math.
Theor. 44: 1-11
Thank you for your attendance
September 2015-Rize, TURKEY