* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Name
Introduction to gauge theory wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electric charge wikipedia , lookup
Lorentz force wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
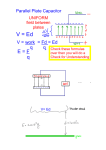
Name: ______________________ Electric Field Gradient Lab Purpose In this lab, you will investigate the electric potential and the electric field associated with different charge distributions. Background Electric potential is often an abstract and confusing concept. The idea of electric force is more intuitive and its extension to electric field, force/unit charge, usually presents less conceptual difficulty. These three quantities, however, are all inter-related, since electric potential is just a mathematical construct that allows electric fields to be treated more easily. Whereas the field is a vector quantity, the potential is a scalar and its mathematics is much simpler. Roughly, one can image the potential to be like the slope of a hill — the steeper it is, the faster its value changes, the more force is exerted. The force points in the direction of steepest descent. You may like to start with this image of electric potential even though the analogy is not perfect. The equipotential plots you produce in this experiment will resemble topographic contour maps. There are several rules to keep in mind about electrical potentials: The value of the potential at a point is the work it takes to move a unit charge from an arbitrary reference position to this point. Once the reference position is chosen it must remain the same for the whole field. The potential on a conductor is everywhere the same if the charges are static. An equipotential surface is a three-dimensional surface on which the electric potential V is the same at every point (like the surface of a conductor). If a test charge q is moved from point to point on such an equipotential surface, the electric potential energy, qV, does not change. Because the potential energy does not change as a test charge moves over an equipotential surface, the electric field can do no work on the charge. It follows that E must be perpendicular to the surface at every point so that the electric force, qE, will always be perpendicular to the displacement of a charge moving around on the surface. In other words: Field lines and equipotential surfaces are always mutually perpendicular. In this experiment, you will look at the field patterns for different electrode configurations. In reality, source charge distributions establish three-dimensional electric fields and potentials. However, to simplify the procedure, we will be investigating the field patterns of electrode configurations constrained to two dimensions, using special conductive paper. The edges of the paper will affect the field, but if we stay several centimeters from the edge, this distortion will not be significant. The fields you map will be very similar to their three-dimensional analogues. Note: two-dimensional fields have equipotential lines instead of equipotential surfaces. [University of Guelph, Guelph, Ontario, Canada www.physics.uoguelph.ca/~omeara/phys1010/expt1.pdf ] Relationships Between V and E: V = -∫E . dr Equipment Power Supply Ruler Multimeter Compass E= dV dr Conductive Paper Procedure 1. Pin the conductive paper to the cardboard. 2. Set the power supply to 10 volts. 3. Make contact with one of the silver paint electrodes with the red power probe. Make contact with the other electrode with the black power probe. This will set up a potential between the two electrodes. 4. With the dial on the Digital Multimeter (DMM) set to the appropriate DC setting (e.g. 20 V), record the measured potential difference between the two electrodes, V. _______________ 5. Divide this number by 5. This will be your voltage increment, V. _______________ 6. Using the DMM, find the equipotential (same voltage) line for V, 4 V, 6 V, etc. by finding multiple points with the same potential difference. Do not measure too close to the edge of the paper. Do not spend too much time in attempting to locate these points of equal potential to high accuracy. 7. Draw your electrode configuration to scale on the white template sheet. From your probing in #6 above, plot the equipotential points and then connect them for each V. These are your equipotential lines. Label each equipotential line with the appropriate voltage. 8. For the parallel plate capacitor, you will need to plot the equipotential lines between the plates, but also determine how the equipotential lines curve beyond the edge of the plates by probing beyond the edges. There will be some analysis questions on the fringing fields. Try to draw your figure and the equipotential lines NEATLY! Using a ruler will help. 9. For the concentric circles mapping, measure r, the distance from the center, to the equipotential line for four points along the +/- x- and +/- y-axes and then take the average. Using Microsoft Word drawing tools, any other drawing program you are familiar with, or a compass, draw the inner and outer circles to scale as bold solid lines. Draw the equipotential circular lines to scale with dotted lines. Option 1: You may due this in Microsoft Word by drawing each circle, then click on the click, go to Format and set the size. Repeat this for each circle and then align them. Option 2: Draw the equipotential lines by hand VERY NEATLY! Option 3: Use a compass to draw your circles. 10. On each of the white template sheets for the preceding two drawings, NEATLY draw the electric field lines based upon the equipotential lines you have already drawn. Remember that the electric field lines are always perpendicular to the equipotential lines (and visa versa). Analysis Parallel Plate Configuration 1. Calculate the magnitude of the electric field between your two plates. 2. How does the electric field varies with distance from one plate to the other near the middle of the plates (i.e. 1/r or 1/r2 or constant, etc.)? 3. Fringing Field A. Describe what happens to the electric field at the edge of the plates? B. How would you expect the ratio of plate length (L) to the separation (d) to affect the fringing at the edge of the plates? (i.e. As L/d increases, do you get more or less fringing?) 4. If the voltage applied between the electrodes was increased by 2X: A. What would happen to the number of equipotential lines (keeping the same V)? B. What would happen to the distance between the equipotential lines? C. What would happen to the potential gradient? D. What would happen to the electric field? Concentric Circles 1. Using Graphical Analysis or Microsoft Excel, A. Plot the potential V versus the distance from the center of the inner electrode r. B. Fit the data to an appropriate function. C. Display the equation of best-fit curve on the graph and then print your graph. 2. Based upon the drawn electric field lines: A. Where is the magnitude of the electric field weakest? Explain your answer. B. Where is the magnitude of the electric field strongest? Explain your answer. Cloud Hanging Over House 1. Apply the red power electrode to the cloud and the black power electrode to the house/ground. Map the equipotential lines and electric field lines for the Cloud Hanging Over House on the white template. Again, draw the house, cloud and equipotential lines NEATLY! 2. Where are the equipotential lines closest together? 3. Where is the electric field the strongest? Explain. 4. Where would the lightning would likely strike?