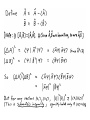* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Heisenberg Uncertainty derivations
Quantum field theory wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Renormalization wikipedia , lookup
Atomic orbital wikipedia , lookup
Identical particles wikipedia , lookup
Double-slit experiment wikipedia , lookup
Quantum computing wikipedia , lookup
Franck–Condon principle wikipedia , lookup
Electron configuration wikipedia , lookup
Quantum group wikipedia , lookup
Quantum machine learning wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Bell's theorem wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Atomic theory wikipedia , lookup
Density matrix wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Quantum key distribution wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum entanglement wikipedia , lookup
History of quantum field theory wikipedia , lookup
Path integral formulation wikipedia , lookup
Probability amplitude wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Quantum teleportation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Renormalization group wikipedia , lookup
Matter wave wikipedia , lookup
Hydrogen atom wikipedia , lookup
Wave–particle duality wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
EPR paradox wikipedia , lookup
Hidden variable theory wikipedia , lookup
Particle in a box wikipedia , lookup
Canonical quantization wikipedia , lookup
THE HEISENBERG UNCERTAINTY PRINCIPLE [Reading: Shankar Chpt. 9 and/or Griffiths 3.5] Overview: Consider a quantum system in state (with eigenvalues and eigenvectors A measurement of yields with probability , and two observables A, B ). . (Likewise for B.) The uncertainty measures the overall spread in possible outcomes of the measurement (i.e., it measures the width of the probability distribution). It is defined as So a system in a general quantum state lacks a well-defined -value. The exception is if happens to be an eigenstate , in which case its -value is unambiguous and hence the uncertainty associated with the measurement is zero. In this case we can say that the system is “in” the state with the definite observable value . Question: When is it possible to say that a quantum system is in a state with definite observable values and ? (i.e., zero uncertainty in either measurement value) Answer: Only if the two observables commute! The reason: Recall that if two operators commute, then they share a common set of eigenvectors. So if a system starts, say, in an eigenstate of , (so that it’s -value is known with zero uncertainty), then it is also automatically in an eigenstate of , and hence its -value is also known precisely (with no uncertainty). Consider instead the case where the two observables don’t commute (and hence have different eigenvectors). Suppose the system is in a state with a definite -value (i.e., it’s in an eigenstate of .) Can it also have a definite -value at the same time? No! For this to happen the system would have to be in a pure eigenstate of . But it’s not! It’s in eigenstate , which we can think of as being made up from some linear combination of the eigenstates. Thus, if were measured, a range of possible -values could result (and thus, ). Said differently, if the initial state of a system is (so that its -value is definite), then a subsequent measurement of B can yield a range of possible values. Once this measurement of is actually made, the system will be thrown into some eigenstate . Hence, the measurement of has actually altered the state of the system from to . Hence, a subsequent re-measurement of can yield a range of possible -values. Observables and are said to be incompatible; a measurement of one “interferes with” measurement of the other. The inability to attribute definite values of two non-commuting observables to a given state of a system is not the result of a “flaw” or inadequate technological advancement in our measuring devices. Even if we had better, more accurate equipment, we couldn’t get around this issue – it’s deeper than that. In short, if two observables don’t commute, then there is no such thing as a state with a well-defined value and -value! The uncertainty principle captures this idea! Loosely speaking, it says the uncertainties in measurements of non-commuting observables can never both be zero! (In fact, there is a lower bound on the product of the uncertainties.) Now let’s be more precise about all this …. APPLICATIONS: Apart from its deep philosophical import, the Heisenberg uncertainty principle also provides a useful tool for making crude, heuristic estimations of things, such as the ground-state energies of various quantum systems. Example 1: Estimating ground-state energy of a SHO Example 2: Estimating ground-state energy of a hydrogen atom Example 3: Estimating ground-state energy of a particle in a box of size L Some other uncertainty relations: 1) In 3-D, (Note: there is no uncertainty relation between, say, observables x and py, nor between, say, x and z, since these pairs commute.) 2) Angular momentum: (We’ll study this later) The Energy—Time “Uncertainty” Principle Here we encounter another uncertainty principle that resembles in form the type we have been discussing: However, it is altogether different in spirit. For one, time “t” is not a dynamical variable represented by a hermitian operator in the same way that position or momentum can be. Hence Δt above means a very different thing than the type of uncertainty associated with an observable that we’ve studied before. Let’s define and derive precisely what we mean. To start, consider an arbitrary observable , and let’s look at how its expectation value evolves in time: For now, we’ll look at one of its implications (directly relating to our new uncertainty principle) – we’ll have more to say about its other implications later. For simplicity, assume the operator on time. In this case, we have in question does not depend explicitly Now let’s recall our generalized uncertainty relation: Note that since the first term on the RHS is positive, we can drop it and the inequality still holds: Choosing relation becomes Finally, defining and using Ehrenfest’s theorem, the uncertainty yields Interpretation and Implication: Δt can be thought of as the amount of time needed for the expectation value of the observable in question to change substantially, i.e., by one standard deviation. Note that Δt depends on which observable of a system is being measured. Note too the following implications of the energy-time uncertainty principle: 1) If the state of the system has a very narrow spread in energy (ΔE small), then Δt is necessarily large, i.e., the expectation values of all observables will evolve slowly. (Indeed, in the extreme case where the system is in an energy eigenstate (ΔE=0), then we recover a result that we already knew, namely, that the expectation value of any observable does not vary in time!) 2) If the expectation value of any observable of a system is changing very rapidly, then the uncertainty principle demands that the system must be in a state with a wide spread of energies. 3) A number of alternate interpretations of the time-energy uncertainty relation also exist, though they may not be quite so “kosher”: e.g. if a system or state of a system has only been in existence for a short period of time Δt, then that system will necessarily have a spread of energies ΔE whose size is dictated by the uncertainty relation. e.g., a system can temporarily “borrow” energy ΔE (in apparent violation of energy conservation), provided it “pays it back” within a time (although some physicists vehemently disagree with this interpretation!) Example (from Constantinescu and Magyari): In a Frank and Hertz experiment, a beam of mono-energetic electrons collide with hydrogen atoms, temporarily raising the atoms from their ground state to their first excited state. (These excited states typically have extremely short “lifetimes” – i.e., the atoms quickly return to their ground state.) It is experimentally observed that, following the collisions, the electrons of the beam are no longer monoenergetic, but rather display a range of energies on the order of 10-6 eV. Why does this happen? What is the mean lifetime of the excited atoms? Answer: Let τ denote the mean life of an excited hydrogen atom. Since the excited state is only localized in time within a precision τ≈Δt, its excitation energy has an uncertainty ΔE ≥ . It is these fluctuations that in turn are responsible for the corresponding energy fluctuations seen in the electron beam. Using the measured value of ΔE given above, we estimate the lifetime of the excited states to be about τ≈3x10-10s. In light of this example, we mention that the spectral lines associated with short-lived excited states of atoms are never infinitely narrow, but rather display a natural width owing to the energy uncertainty associated with their short lives! Example (from Constantinescu and Magyari): The π-meson is associated with the nuclear force, which has an approximate range of about 1.4 Fermi (1 Fermi =10-13cm). Assuming that it cannot travel faster than c, estimate the mass of the π-meson. The minimum-uncertainty wave packet The position-momentum uncertainty principle is Question: What shape wavefunction uncertainty limit? Answer: A gaussian! will hit the minimum- Here’s the justification: So a general gaussian wavepacket (centered at x0 with average momentum p0) hits the uncertainty limit! *Caution: if, at some instant in time, a wavefunction is gaussian, then we know that, at that moment, . However, as time passes the wavefunction will evolve according to the Schroedinger equation, and in general will not remain gaussian. An interesting exception occurs in the case of the quantum harmonic oscillator: Here, it is possible to find mimimum uncertainty states that remain minimum-uncertainty states throughout time (i.e., at any instant they look gaussian, though not necessarily the same gaussian as they were before). These states are called “coherent states.” Question: Can you show that coherent states are eigenstates of the lowering operator? (Griffiths’ problem 3.35 walks you through this.) Approaching the Classical Limit Warm-up Question: In our earlier study of a particle encountering a step potential, we found that, quantum mechanically, when E>V0, a portion of the wave is reflected. For example, if E=2V0, then quantum mechanics predicts R=0.17 – hence we should see reflection a moderate fraction of the time. But if we actually go to the lab and set up a potential that approximates the above step potential and then send in a baseball with twice the energy of the step, we in fact will NOT observe any reflection – we’ll just observe the classical result of 100% transmission! Moreover, even if we replace the baseball by an electron, we still may not observe any reflection! So we must face the question “Under what conditions will classical physics suffice as a good approximation to our quantum world, and when must we use quantum mechanics? Different approaches to understanding the classical-quantum correspondence: 1) Ehrenfest’s theorem: Setting (where we used the fact that Similarly, letting and letting ). , Ehrenfest’s theorem yields yields Note the striking similarity to Hamilton’s equations (i.e., Newtons IInd law). The only difference is the presence of the brackets (i.e., the expectation values) in the quantum case. In particular, if we were allowed to replace then the expectation values <x> and <p> would precisely obey the Newton’s laws of classical physics! So when is the above approximation valid? -- Basically, when the potential V(x) or force (as defined by the derivative of the potential) don’t vary much over the “size” (i.e., spread in x) of the wavepacket. In this case, classical physics is a good approximation (and we don’t need quantum). 2) A closely related way of thinking about the classical limit is as follows: Look at the de Broglie wavelength of the particle in question: If the potential V(x) of the problem doesn’t vary much over a distance scale defined by the particle’s de Broglie wavelength, then we recover classical physics. (If the potential does vary rapidly over length scale λ, then we expect to observe quantum effects.) So go back to our example of a particle going over a step potential. First note that in practice we can never have a true (infinitely abrupt) “step” in a potential – the transition region (where the potential rapidly rises from 0 to V0) may be narrow but never infinitely so. Now suppose the incident particle we send toward the step is a 100eV electron. Since we would thus expect that if the transition region of the potential is comparable to (or narrower than) about 10-10m, then we should observe quantum reflection about 17% of the time! But if the transition region is much wider than 10-10m (which is about an atomic radius), then we will not see any such quantum effects. 3) It is also sometimes said that If one likes, this can be regarded as simply another way of interpreting lim λ 0 (since λ=h/p). But it can also be thought of slightly differently. In particular, as h 0, quantum uncertainty goes away! (i.e., think of Δx Δp ≥ .) This notion that the classical regime corresponds to the limit h 0 can be formalized using the so-called WKB approximation, in which the solution to the Schroedinger equation is found in powers of . This method is described in your texts (Shankar or Griffiths), but we will not be discussing it this semester. 4) The “Bohr Correspondence Principle” This basically says that we “recover” (in a certain sense) classical mechanics as we go to higher and higher quantum numbers. This is best seen via an illustration (here we’ll use the eigenstate of the simple harmonic oscillator): Comparison of Quantum Probability (n=20 state) and Classical Probability