Download 2014_12_19.Topic 11INK

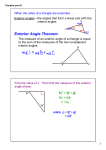
TOPIC 11
Triangles and polygons
We can proceed directly from the results we learned about parallel lines and their associated
angles to the ideas concerning triangles.
An essential question is a question whose answer is not obvious, but it is a vitally important
question that we continue to ponder.
Essential question: Why are triangles so important in the study of
geometry?
We will spend more time studying triangles than any other single topic. Why?
Let’s review the definitions:
1.
What is a triangle?
2.
What is an isosceles triangle?
3.
What is an equilateral triangle?
4.
What is a scalene triangle?
5.
What is a scalene triangle?
6.
What is an acute triangle?
7.
What is an obtuse triangle?
8.
What is a right triangle?
What can we discover that is true about a triangle? One well-known result concerns the sum of
the angles of a triangle. We will do this with a paper triangle in class … a sort of kinesthetic
proof. In a more formal way, we will work through a written proof.
Topic 11 (Triangles and Polygons)
page 2
Given: Δ ABC
Prove: m< 1 + m< 2 + m< 3 = 180
 
Draw ECD || AB
1.
2.
< 2  ______
2.
3.
< 3  ______
3.
4.
m< 2 = m < _______
m< 3 = m < _______
4.
5.
< ____ is supp to < ACD
5.
6.
m < ____ + m < ACD = 180
6.
7.
m< 1 + m < ____ = m < ACD
7.
8.
m < ACE + m < ____ + m < ____= 180
8.
9.
m< 2 + m < 1 + m < BCD = 180
9.
10.
m< 1 + m < 2 + m < 3 = 180
10.
Proof: 1.
Def supp
angle addition postulate
QED
Is the parallel postulate necessary in this proof? (We use this as the parallel postulate: If
corresponding angles are congruent, then lines are parallel.) As an implication of this fact, we
accept as true the fact that there is only one line through a point which is parallel to a given line.
We will discuss this assumption in more detail in a few weeks.
Next, we will look at other angles associated with triangles. An exterior angle is an angle which
is adjacent to one of the interior angles of a triangle. It is formed by extending one of the line
segment sides of a triangle.
Topic 11 (Triangles and Polygons)
Sketchpad Investigation:
1.
2.
Draw a triangle as shown.
Measure angles as needed to answer these questions,
using Sketchpad evidence.
3.

Questions:
How is < 1 related to the interior angles of the triangle?

What is the sum of the three exterior angles in a triangle?

Can a triangle have ________
a) 3 obtuse interior angles
b) 2 obtuse interior angles
c) 1 obtuse interior angle
d) 3 congruent, acute interior angles
e) 2 congruent, acute interior angles
f)
g)
h)
i)
j)
3 obtuse exterior angles
2 obtuse exterior angles
1 obtuse exterior angle
3 congruent, obtuse exterior angles
2 congruent, obtuse exterior angles
page 3
Topic 11 (Triangles and Polygons)
4.
5.
page 4

Draw a right triangle, ΔABC. Keep BC unchanged, but move A along AC . Describe
what happens to m< 1 , m< 2, m < 3, and m< 4.
In the right triangles that you constructed above, can m< 1 in
one of the right triangles be
twice as large as m< 1 in another one, as you move A along AC ? If so, compare the
lengths of AC in the two triangles?
One proof
How is one of the exterior angles of a triangle related to the two remote interior angles? Prove
your conclusion.
Topic 11 (Triangles and Polygons)
page 5
Polygons …what are they, and how do we use what we
already know to learn about their properties?
To produce polygons, we need to have some ground rules:
 The figure has to be bounded by line segments (but the segments do not all have to be
congruent), and the line segments can only intersect at their endpoints.
 The figure must be closed. (There has to be an interior and an exterior? How do we
know which is the interior?)
 Only two segments can intersect at each endpoint. (If more than two segments are drawn
at a vertex, then the excess over two may be “diagonals”.)
 There are convex polygons and concave polygons.
Do some research to find the names of polygons. They are labelled according to the number of
sides that they have.
N
Name
1
2
3
4
5
6
7
8
9
10
11
12
13
20
40
52
73
n
Triangle
Quadrilateral
Pentagon
Hexagon
Heptagon
Octagon
Nonagon
Decagon
Henneagon
Dodecagon
13-gon
Icosagon
40-gon
52-gon
73-gon
n-gon
Second name
(maybe)
Sexagon
Septagon
Topic 11 (Triangles and Polygons)
page 6
Look up the definitions of equilateral and equiangular. Look up the definition of a regular
polygon.
Draw an equilateral but non- equiangular quadrilateral.
Draw an equiangular but non- equilateral quadrilateral.
Draw an equilateral and equiangular quadrilateral.
Draw an equilateral but non- equiangular hexagon.
Topic 11 (Triangles and Polygons)
page 7
Draw an equiangular but non- equilateral hexagon.
Draw an equilateral and equiangular hexagon.
Draw a regular triangle.
Draw a regular quadrilateral.
Draw a regular pentagon
Draw a regular hexagon.
Topic 11 (Triangles and Polygons)
page 8
Looking at the angles in polygons:
Draw a quadrilateral. Make it scalene and not regular for now. Pick one vertex, and draw all of
the diagonals from that vertex. (A diagonal is a line segment which connects non-consecutive
vertices.)
How many triangles are formed?
How many degrees are in the sum of the angles of each triangle?
Therefore, what is the sum of the measures of the interior angles of the quadrilateral?
Do you think that result would be different had you drawn a parallelogram? A square? A
rhombus?
Draw a pentagon. Make it scalene and not regular for now. Pick one vertex, and draw all of the
diagonals from that vertex.
Topic 11 (Triangles and Polygons)
page 9
How many triangles are formed?
How many degrees are in the sum of the angles of each triangle?
Therefore, what is the sum of the measures of the interior angles of the quadrilateral?
Do you think that result would be different had you drawn a regular pentagon?
Continue the process for other polygons. You are thinking inductively, looking for a pattern.
N
3
4
5
6
7
8
9
10
n
Name
Sum of interior angles
Topic 11 (Triangles and Polygons)
page 10
Open a Sketchpad document. Draw a convex quadrilateral. Try not to make it too special.
Extend each side to form one exterior angle, as shown. Measure each of the four exterior angles,
and calculate the sum of these exterior angles. Contort your quadrilateral and observe what
happens to the sum of the exterior angles.
Open a new sketch. Do the same investigation with a convex pentagon.
In a regular polygon, since the interior angles all have equal measure, then the measure of each
interior angle can be calculated by dividing the sum of the interior angles by the number of
sides.
1.
Calculate the size of each interior angle in a regular pentagon. Show your work.
2.
Calculate the size of each interior angle in a regular hexagon. Show your work.
Topic 11 (Triangles and Polygons)
page 11
3.
Calculate the size of each interior angle in a regular nonagon. Show your work.
4.
Calculate the size of each interior angle in a regular 42-gon. Show your work.
The same idea is used to find the size of each exterior angle in a regular polygon.
5.
Calculate the size of each exterior angle in a regular pentagon. Show your work.
6.
Calculate the size of each exterior angle in a regular hexagon. Show your work.
7.
Calculate the size of each exterior angle in a regular nonagon. Show your work.
Summarize the calculation of these angles for an n-gon:
Sum of the measures of the interior angles =
Measure of each interior angle (regular polygons) =
Topic 11 (Triangles and Polygons)
page 12
Sum of the measures of the exterior angles =
Measure of each exterior angle (regular polygons) =
Design an Excel spreadsheet to see the patterns in the angles in polygons. (You will be using
your laptop to do this.) The first rows should look like this, and you will be shown how to enter
formulas in a spreadsheet.
Angles in Polygons # of sides ## of sum of sum of angles int<'s ext <'s 3 1
180
360
4 2
360
360
5 3
540
360
6 4
720
360
7 5
900
360
8 6
1080
360
9 7
1260
360
10 8
1440
360
11 9
1620
360
12 10
1800
360
GULAR each int angle 60
90
108
120
128.5714
135
140
144
147.2727
150
each ext angle 120 90 72 60 51.42857 45 40 36 32.72727 30 Observations:
 What happens in the sequence of the sum of the interior angles?

What happens in the sequence of the sum of the exterior angles?
Topic 11 (Triangles and Polygons)
page 13

What does the size of each interior angle (regular polygons) sem to approach as n gets
really large?

What does the size of each exterior angle (regular polygons) sem to approach as n gets
really large?

How many different kinds of regular polygons have exterior angles which are integers?

How many different kinds of regular polygons have interior angles which are all less than
1510?
How Big are the ANGLES in TRIANGLES &
POLYGONS
Here are some triangles and polygons whose angles need to be calculated. Use the new formulas
that you have learned and verified.
1.
Verify that the sum of the exterior angles, taken one at each vertex, of any n-gon is 3600.
(This can be done in an algebraic flavor.)
Topic 11 (Triangles and Polygons)
page 14
2.
The measures of the three angles of a triangle are in the ratio 2:4:9. Find the measure of
each angle. (Hint: Call the measures of the angles 2x, 4x, and 9x).
3.
The measures of the three angles of a triangle are in the ratio 2:3:5. Find the measure of
the smallest exterior angle.
4.
Four of the angles in a pentagon measure 45, 65, 128, and 147. What is the measure of
the fifth angle?
5.
Two of the interior angles of a quadrilateral have measure 360 and 840. The other two
angles are in the ratio 3:5. Find the measure of the other two interior angles as well as the
second to largest exterior angle.
6.
The measure of one of the acute angles of a right triangle is 150 less than twice the
measure of the other acute angle. Find the measure of each of the acute angles.
Topic 11 (Triangles and Polygons)
7.
Find the measures of the numbered angles in the drawing. It is given that AB  BC .
m<1=
m<2=
m<3=
m<4=
8.
page 15
Okay, not all numerical problems …..
Given: The plane figure
Prove: r + s = t + q
Topic 11 (Triangles and Polygons)
page 16
9.
Each of the five angles of a convex hexagon measures 1300. What is the measure of the
sixth interior angle?
10.
How many sides does a regular convex polygon have if one exterior angle has measure
240 ?
11.
What is the measure of an interior angle of a regular polygon with 12 sides?
12.
If each interior angle of a regular polygon has a measure of 1700, how many sides does it
have?
13.
Is it possible for a regular polygon to have interior angles whose measure is _____?
(Describe why or why not.)
a) 100
d)
500
b)
450
c)
0.50
Topic 11 (Triangles and Polygons)
page 17
14.
If each exterior angle of a regular polygon has measure 300, what is the sum of the
measure of the interior angels of that polygon?
15.
Discover a formula for the total number of diagonals that can be drawn from all vertices
in a convex n-gon.
16.
One angle of a triangle has measure 450, and the other two angles are in the ratio 1:2.
Find the other two angles.
17.
Find the angle between the two bisectors of the acute angles of a right triangle.
18.
An exterior angle of a triangle has measure 1300. One remote interior angle is 360 more
than the other remote inter angle. Find the measures of those remote interior angles.
Topic 11 (Triangles and Polygons)
page 18
19.
The sum of an angle and twice its complement is 1460. Find the measure of the angle.
20.
Find the first instance where an n-gon and an n+1-gon contribute one interior angle each
whose sum exceeds 2700. (Assume that the polygons are sitting adjacent to each other,
and they have congruent sides.)
21.
Write three examples of combinations of polygons whose interior angles share a vertex
and yet do not intersect so that the sum of one each of their interior angles does not
exceed 3600.
ISOSCELES TRIANGLES…..
Two angles of an isosceles triangle are congruent. (Accept this right now without proof. The
verification will come in a few weeks.).
The congruent angles are called base angles,
and the third angle is called the vertex angle.
The congruent sides are called legs, and the
third side is called the base.
Vertex angle
leg
leg
base angle
base angle
base
Topic 11 (Triangles and Polygons)
22.
m < C = 1000
m< A = _____
m< B = _____
23.
m < C = 460
m< A = _____
m< B = _____
24.
m < 1 = 1100
m< 2 = _____
m< 3 = ______
m < 4 = ______
25.
m < 4 = 820
m< 1 = _____
m< 2 = ______
m < 3 = ______
26.
m < 2 = 3x + 10
m < 4 = 2x + 40.
Solve for x.
page 19
Topic 11 (Triangles and Polygons)
27.
m < 1 = ______
28.
x = ________
y = ________
(regular octagon)
29.
Find the measures of the numbered angles.
(regular pentagon)
page 20
Topic 11 (Triangles and Polygons)
page 21
30.
The supplement of an angle is 10 0 more than three times its complement. Find the angle.
31.
Two angles in a triangle sum to 2
of the measure of the third angle. One of those two
3
angles is 20 more than the other. Find the measure of the largest angle in the triangle.
Problems are from Mathematics Review Exercises (Smith and Fagan, Ginn and Company, 1961), Modern School
Mathematics: Geometry (Jurgenson, Donnelly, Dolciani,Hougling Mifflin, 1972), and your teacher on a sunny, cold
Friday afternoon.
Definition: A tessellation is a plane filling combination of shapes. (There are no gaps nor any
overlaps of the shapes).
This means that the interior angles that surround a point have to sum to 360 exactly. For
example, four squares can surround a point. Since each square has an interior angle with
measure 900, then the sum of four of these with be exactly 3600. It is also true that two regular
octagons and one square will surround a point. This is because the interior angles are 135, 135,
and 90, and 135 + 135 + 90 = 360.
Topic 11 (Triangles and Polygons)
page 22
A tessellation is called a regular tessellation if only one kind of regular polygon is used (such as
four squares), and the symbol is 4-4-4-4 (for “square-square-square-square”). A tessellation is
called a semi-regular tessellation if different kinds of regular polygons are used, but the
configuration at every vertex is identical throughout the tiling. The tessellation with two
octagons and one square above is an example, and its symbol is 8-8-4 (or 8-4-8 or 4-8-8: all are
the same). A demi-regular tessellation is one made of different kinds of regular polygons are
used, but the configuration at various vertices is not identical throughout the tiling.
Make a list of all of the regular tessellations, using symbols like 4-4-4-4. Use the cut out tiles to
experiment.
Make a list of all of the semi-regular and demi-regular tessellations that you can think of. Use the
cut out tiles to experiment. (You do not have to worry about whether they are “semi” or “demi”
regular.)
Topic 11 (Triangles and Polygons)
Here are some more complex tessellations. Describe what happens at various vertices.
page 23
Topic 11 (Triangles and Polygons)
Tessellations are from http://library.thinkquest.org/16661/templates/index.html .
page 24