Geometry Module - Rice University Math
... diverse student populations than the passive, teacher-centered learning methods which have dominated mathematics instruction in the past. The Geometry Module materials are consistent with these recommendations. The Geometry Module is based on the van Hiele model of geometric thought. NCTM in its Sta ...
... diverse student populations than the passive, teacher-centered learning methods which have dominated mathematics instruction in the past. The Geometry Module materials are consistent with these recommendations. The Geometry Module is based on the van Hiele model of geometric thought. NCTM in its Sta ...
Tennessee Mathematics Standards
... translations, glide reflections, and dilations). 3108.4.32 Recognize, identify and apply types of symmetries (point, line, rotational) of two- and three- dimensional figures. 3108.4.33 Use transformations to create and analyze tessellations and investigate the use of tessellations in architecture, ...
... translations, glide reflections, and dilations). 3108.4.32 Recognize, identify and apply types of symmetries (point, line, rotational) of two- and three- dimensional figures. 3108.4.33 Use transformations to create and analyze tessellations and investigate the use of tessellations in architecture, ...
LSU College Readiness Program COURSE
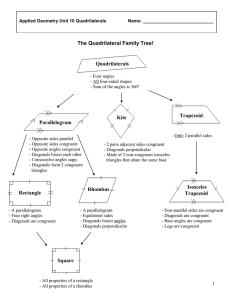
... Use properties of diagonals of rhombuses, rectangles, and squares Use properties of diagonals to form rhombuses, rectangles, and squares 6.5 Trapezoids and Kites (26) Use properties of trapezoids Use properties of kites ...
... Use properties of diagonals of rhombuses, rectangles, and squares Use properties of diagonals to form rhombuses, rectangles, and squares 6.5 Trapezoids and Kites (26) Use properties of trapezoids Use properties of kites ...
CHAPTER 1. LINES AND PLANES IN SPACE §1. Angles and
... 1.13.Through point O2 , draw line l10 parallel to l1 . Let Π be the plane containing lines l2 and l10 ; A01 the projection of point A1 to plane Π. As follows from Problem 1.11, line A01 A2 constitutes equal angles with lines l10 and l2 and, therefore, triangle A01 O2 A2 is an equilateral one, hence, ...
... 1.13.Through point O2 , draw line l10 parallel to l1 . Let Π be the plane containing lines l2 and l10 ; A01 the projection of point A1 to plane Π. As follows from Problem 1.11, line A01 A2 constitutes equal angles with lines l10 and l2 and, therefore, triangle A01 O2 A2 is an equilateral one, hence, ...
Lesson 9-2
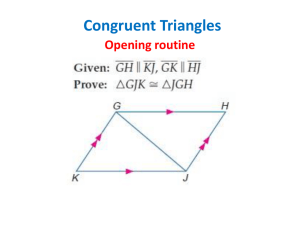
... Congruent: Two figures are congruent when coinciding at all points when superimposed. Side-Side-Side (SSS) Postulate: If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent. Side-Angle-Side (SAS) Postulate: If two sides and the included angl ...
... Congruent: Two figures are congruent when coinciding at all points when superimposed. Side-Side-Side (SSS) Postulate: If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent. Side-Angle-Side (SAS) Postulate: If two sides and the included angl ...
Geometry - Hickman County Schools
... geometry (e.g. rounding and pattern identification in activities, and manipulatives to develop the measurement, the relationship of pi to other rational language and the concepts of geometry, and irrational numbers) including specialized vocabulary (e.g. graphing calculators, interactive geometry ...
... geometry (e.g. rounding and pattern identification in activities, and manipulatives to develop the measurement, the relationship of pi to other rational language and the concepts of geometry, and irrational numbers) including specialized vocabulary (e.g. graphing calculators, interactive geometry ...
TO CONSTRUCT AN ANGLE CONGRUENT TO A GIVEN ANGLE
... Determine which formulas (Distance, midpoint, or slope) you need to answer the question. Write out the formulas. You MUST use distance, midpoint, or slope formulas to receive credit for the problem. Substitute the numbers into the formulas to show your work. Be organized and neat when showing your w ...
... Determine which formulas (Distance, midpoint, or slope) you need to answer the question. Write out the formulas. You MUST use distance, midpoint, or slope formulas to receive credit for the problem. Substitute the numbers into the formulas to show your work. Be organized and neat when showing your w ...
Tessellation

A tessellation of a flat surface is the tiling of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellations can be generalized to higher dimensions and a variety of geometries.A periodic tiling has a repeating pattern. Some special kinds include regular tilings with regular polygonal tiles all of the same shape, and semi-regular tilings with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called ""non-periodic"". An aperiodic tiling uses a small set of tile shapes that cannot form a repeating pattern. In the geometry of higher dimensions, a space-filling or honeycomb is also called a tessellation of space.A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. Such tilings may be decorative patterns, or may have functions such as providing durable and water-resistant pavement, floor or wall coverings. Historically, tessellations were used in Ancient Rome and in Islamic art such as in the decorative tiling of the Alhambra palace. In the twentieth century, the work of M. C. Escher often made use of tessellations, both in ordinary Euclidean geometry and in hyperbolic geometry, for artistic effect. Tessellations are sometimes employed for decorative effect in quilting. Tessellations form a class of patterns in nature, for example in the arrays of hexagonal cells found in honeycombs.