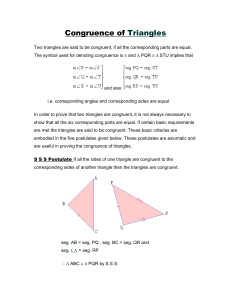
Properties and Conditions for Kites and Trapezoids
... A kite is a quadrilateral with two distinct pairs of congruent consecutive sides. A trapezoid is a quadrilateral with at least one pair of parallel sides. These definitions may not be the same as definitions in other textbooks. Such decisions about definitions are somewhat arbitrary. Variations of d ...
... A kite is a quadrilateral with two distinct pairs of congruent consecutive sides. A trapezoid is a quadrilateral with at least one pair of parallel sides. These definitions may not be the same as definitions in other textbooks. Such decisions about definitions are somewhat arbitrary. Variations of d ...
4 blog notes congruent triangles
... same SHAPE (similar), but does NOT work to also show they are the same size, thus congruent! Consider the example at the right. ...
... same SHAPE (similar), but does NOT work to also show they are the same size, thus congruent! Consider the example at the right. ...
9 . 5 Properties and Conditions for Kites and Trapezoids
... In the kite ABCD you constructed in Steps D–F, look at ∠CDE and ∠ADE. What do you notice? _ Is this true for ∠CBE and ∠ABE as well? How can you state this in terms of diagonal AC and the pair of non-congruent opposite angles ∠CBA and ∠CDA? ...
... In the kite ABCD you constructed in Steps D–F, look at ∠CDE and ∠ADE. What do you notice? _ Is this true for ∠CBE and ∠ABE as well? How can you state this in terms of diagonal AC and the pair of non-congruent opposite angles ∠CBA and ∠CDA? ...
Periodic Billiard Paths in Triangles
... Let a point move on a frictionless plane bounded by a triangle If it hits a corner (a vertex), then it stops If it hits a side (an edge), then it changes its direction such that the angle of reflection is equal to the angle of incidence The path that the point follows is called a billiard path An in ...
... Let a point move on a frictionless plane bounded by a triangle If it hits a corner (a vertex), then it stops If it hits a side (an edge), then it changes its direction such that the angle of reflection is equal to the angle of incidence The path that the point follows is called a billiard path An in ...
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right. A Penrose tiling has many remarkable properties, most notably:It is non-periodic, which means that it lacks any translational symmetry. It is self-similar, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through ""inflation"" (or ""deflation"") and any finite patch from the tiling occurs infinitely many times.It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction and its diffractogram reveals both the fivefold symmetry and the underlying long range order.Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions or subdivision rules, cut and project schemes and coverings.







![[edit] Star polyhedra](http://s1.studyres.com/store/data/000129689_1-21c3cefe8dffc208c8fed163027e6a92-300x300.png)