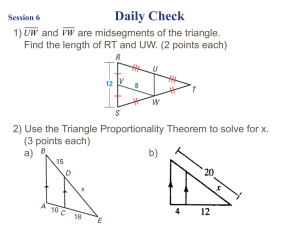
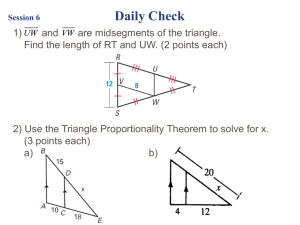
Determine whether the triangles are similar. If so, write a similarity
... Determine whether the triangles are similar. If so, write a similarity statement. If not, what would be sufficient to prove the triangles similar? Explain your reasoning. ...
... Determine whether the triangles are similar. If so, write a similarity statement. If not, what would be sufficient to prove the triangles similar? Explain your reasoning. ...
Triangles
... Areas and altitudes of similar triangles: If you have two triangles it is an interesting problem to see if the triangles are related in any way. Here is the way to determine if the triangles are related: Establish whether or not the triangles both fall into one of the basic sets: scalene, purely is ...
... Areas and altitudes of similar triangles: If you have two triangles it is an interesting problem to see if the triangles are related in any way. Here is the way to determine if the triangles are related: Establish whether or not the triangles both fall into one of the basic sets: scalene, purely is ...
Lesson 17: The Side-Angle-Side (SAS) and Side-Side
... There is no information about the angle measures other than the right angle, so we cannot use AA to conclude the triangles are similar. We only have information about two of the three side lengths for each triangle, so we cannot use SSS to conclude they are similar. If the triangles are similar, we ...
... There is no information about the angle measures other than the right angle, so we cannot use AA to conclude the triangles are similar. We only have information about two of the three side lengths for each triangle, so we cannot use SSS to conclude they are similar. If the triangles are similar, we ...
Geometry Module 2, Topic C, Lesson 17: Teacher
... There is no information about the angle measures other than the right angle, so we cannot use AA to conclude the triangles are similar. We only have information about two of the three side lengths for each triangle, so we cannot use SSS to conclude they are similar. If the triangles are similar, we ...
... There is no information about the angle measures other than the right angle, so we cannot use AA to conclude the triangles are similar. We only have information about two of the three side lengths for each triangle, so we cannot use SSS to conclude they are similar. If the triangles are similar, we ...
Unit 31 Angles and Symmetry
... Now c and d can be found using corresponding angles. The angle c and the 70° angle are corresponding angles, so c = 70° . The angle d and the 60° angle are corresponding angles, so d = 60° . © CIMT and e-Learning Jamaica ...
... Now c and d can be found using corresponding angles. The angle c and the 70° angle are corresponding angles, so c = 70° . The angle d and the 60° angle are corresponding angles, so d = 60° . © CIMT and e-Learning Jamaica ...
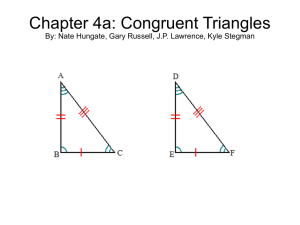
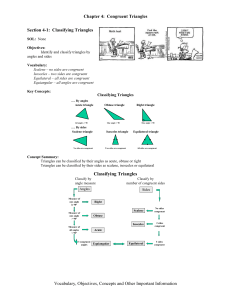
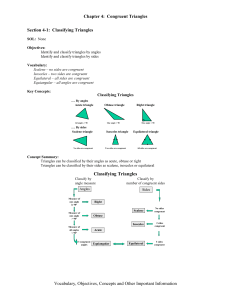
Chapter 4: Congruent Triangles Classifying Triangles
... SOL: None Objectives: Apply the Angle Sum Theorem Apply the Exterior Angle Theorem Vocabulary: Exterior Angle: is formed by one side of a triangle and the extension of another side Remote Interior Angle: interior angles not adjacent to the given exterior angle Corollary: a statement that can be easi ...
... SOL: None Objectives: Apply the Angle Sum Theorem Apply the Exterior Angle Theorem Vocabulary: Exterior Angle: is formed by one side of a triangle and the extension of another side Remote Interior Angle: interior angles not adjacent to the given exterior angle Corollary: a statement that can be easi ...
Chapter 4
... SOL: None Objectives: Apply the Angle Sum Theorem Apply the Exterior Angle Theorem Vocabulary: Exterior Angle: is formed by one side of a triangle and the extension of another side Remote Interior Angle: interior angles not adjacent to the given exterior angle Corollary: a statement that can be easi ...
... SOL: None Objectives: Apply the Angle Sum Theorem Apply the Exterior Angle Theorem Vocabulary: Exterior Angle: is formed by one side of a triangle and the extension of another side Remote Interior Angle: interior angles not adjacent to the given exterior angle Corollary: a statement that can be easi ...
STRAND F: GEOMETRY F1 Angles and Symmetry Text
... Now c and d can be found using corresponding angles. The angle c and the 70° angle are corresponding angles, so c = 70° . The angle d and the 60° angle are corresponding angles, so d = 60° . ...
... Now c and d can be found using corresponding angles. The angle c and the 70° angle are corresponding angles, so c = 70° . The angle d and the 60° angle are corresponding angles, so d = 60° . ...
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right. A Penrose tiling has many remarkable properties, most notably:It is non-periodic, which means that it lacks any translational symmetry. It is self-similar, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through ""inflation"" (or ""deflation"") and any finite patch from the tiling occurs infinitely many times.It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction and its diffractogram reveals both the fivefold symmetry and the underlying long range order.Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions or subdivision rules, cut and project schemes and coverings.