File - Mr. Rice`s advanced geometry class
... also a right angle. It is also provided that PQ is congruent to QR thus that the hypotenuses are congruent. For the legs, you can use the reflexive property QS is congruent to QS. 3. SAS Postulate. Since it is provided that PQ is congruent to QR and you can prove that angle QPS is congruent to QRS ...
... also a right angle. It is also provided that PQ is congruent to QR thus that the hypotenuses are congruent. For the legs, you can use the reflexive property QS is congruent to QS. 3. SAS Postulate. Since it is provided that PQ is congruent to QR and you can prove that angle QPS is congruent to QRS ...
Triangles and Congruence
... According to legend, one of Napoleon’s officers used congruent triangles to estimate the width of the river. On the riverbank, the officer stood up straight and lowered the visor of his cap until the farthest thing he could see was the edge of the opposite bank. He then turned and noted the spot on ...
... According to legend, one of Napoleon’s officers used congruent triangles to estimate the width of the river. On the riverbank, the officer stood up straight and lowered the visor of his cap until the farthest thing he could see was the edge of the opposite bank. He then turned and noted the spot on ...
Proving Triangles and Quadrilaterals are Special
... Consider ΔTAP'. Since two sides are equal, it is isosceles, so ∠RTA = ∠RP'A. RP is also rotated 180˚ around a point not on the line, so image is parallel to pre-image. That is, PR || P'A. Using transversal TP', we see that ∠RP'A = ∠TRP. Thus ∠RTA = ∠RP'A= ∠TRP. Because two angles in ΔTRB are eq ...
... Consider ΔTAP'. Since two sides are equal, it is isosceles, so ∠RTA = ∠RP'A. RP is also rotated 180˚ around a point not on the line, so image is parallel to pre-image. That is, PR || P'A. Using transversal TP', we see that ∠RP'A = ∠TRP. Thus ∠RTA = ∠RP'A= ∠TRP. Because two angles in ΔTRB are eq ...
4 - Wsfcs
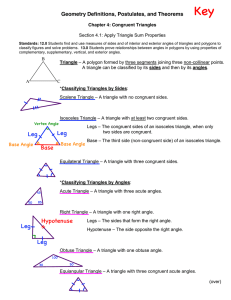
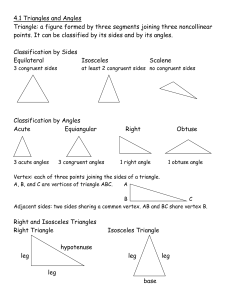
... Congruent: two geometric figures that have exactly the same size and shape. When two figures are congruent, there is a correspondence between their angles and sides such that corresponding sides are congruent and corresponding angles are congruent. ABC PQR ...
... Congruent: two geometric figures that have exactly the same size and shape. When two figures are congruent, there is a correspondence between their angles and sides such that corresponding sides are congruent and corresponding angles are congruent. ABC PQR ...
Geometry - Harrison High School
... between two congruent angles AAS – Pairs of congruent angles and the side not contained between them. SAS - Pairs of congruent angles contained between two congruent sides SSS - Three pairs of congruent sides ...
... between two congruent angles AAS – Pairs of congruent angles and the side not contained between them. SAS - Pairs of congruent angles contained between two congruent sides SSS - Three pairs of congruent sides ...
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right. A Penrose tiling has many remarkable properties, most notably:It is non-periodic, which means that it lacks any translational symmetry. It is self-similar, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through ""inflation"" (or ""deflation"") and any finite patch from the tiling occurs infinitely many times.It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction and its diffractogram reveals both the fivefold symmetry and the underlying long range order.Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions or subdivision rules, cut and project schemes and coverings.