Triangle Tiling IV: A non-isosceles tile with a 120 degree angle
... congruent to T , overlapping only at their boundaries. The triangle T is the “tile”. The tile may or may not be similar to ABC. We wish to understand possible tilings by completely characterizing the triples (ABC, T, N ) such that ABC can be N -tiled by T . In particular, this understanding should e ...
... congruent to T , overlapping only at their boundaries. The triangle T is the “tile”. The tile may or may not be similar to ABC. We wish to understand possible tilings by completely characterizing the triples (ABC, T, N ) such that ABC can be N -tiled by T . In particular, this understanding should e ...
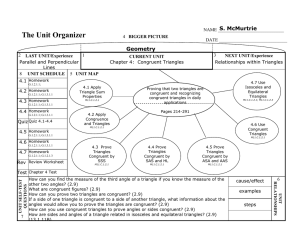
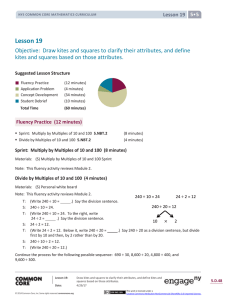
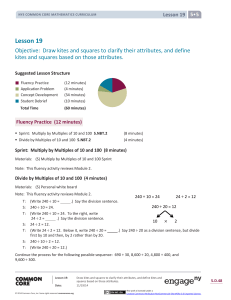
6-2 Properties of Parallelograms 6-3 Conditions for Parallelograms
... A trapezoid is a quadrilateral with exactly one pair of parallel sides. o The parallel sides are called bases and the non-parallel sides are called legs o Base angles are the consecutive angles which have a base as a common side. o An isosceles trapezoid has legs that are congruent Similar to an i ...
... A trapezoid is a quadrilateral with exactly one pair of parallel sides. o The parallel sides are called bases and the non-parallel sides are called legs o Base angles are the consecutive angles which have a base as a common side. o An isosceles trapezoid has legs that are congruent Similar to an i ...
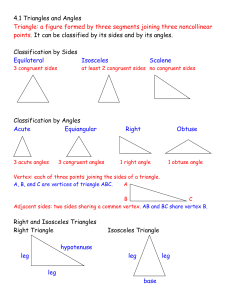
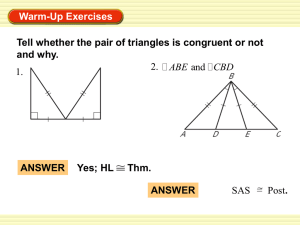
11.1 Similar and Congruent Triangles
... and using congruent and similar shapes make calculations and design work easier. For example, in most design work, rather than using different shapes, a few shapes are copied and used in different positions and/or produced in different sizes to complete the design. When a shape is obtained from anot ...
... and using congruent and similar shapes make calculations and design work easier. For example, in most design work, rather than using different shapes, a few shapes are copied and used in different positions and/or produced in different sizes to complete the design. When a shape is obtained from anot ...
Name
... 7) _____ It is impossible for a square to also be a rectangle. 8) _____ A trapezoid is a parallelogram. 9) _____ Every trapezoid is also a quadrilateral. 10) _____ A quadrilateral can have more than four angles. 11) _____ The trapezoid is the only quadrilateral that is NOT a parallelogram. 12) _____ ...
... 7) _____ It is impossible for a square to also be a rectangle. 8) _____ A trapezoid is a parallelogram. 9) _____ Every trapezoid is also a quadrilateral. 10) _____ A quadrilateral can have more than four angles. 11) _____ The trapezoid is the only quadrilateral that is NOT a parallelogram. 12) _____ ...
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right. A Penrose tiling has many remarkable properties, most notably:It is non-periodic, which means that it lacks any translational symmetry. It is self-similar, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through ""inflation"" (or ""deflation"") and any finite patch from the tiling occurs infinitely many times.It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction and its diffractogram reveals both the fivefold symmetry and the underlying long range order.Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions or subdivision rules, cut and project schemes and coverings.