Download SIDE - Mona Shores Blogs

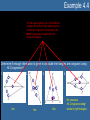
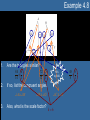
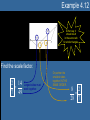
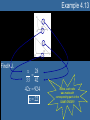
Unit 4
Congruent & Similar Triangles
Lesson 4.1
Day 1:
Congruent Triangles
Lesson 4.1 Objectives
• Identify corresponding parts of congruent figures.
• Characterize congruent figures based on a
congruence statement.
• Identify congruent triangles by using congruence
theorems and postulates. (G2.3.1)
Congruent Triangles
• When two triangles are congruent, then
– Corresponding angles are congruent.
– Corresponding sides are congruent.
•
Corresponding, remember, means that objects are in the
same location.
– So you must verify that when the triangles are drawn in the same
way, what pieces match up?
Naming Congruent Parts
That way we know:
We also know:
A   D ,
D
A
AB  DE ,
B  E ,
BC  EF ,
and C  F.
F
B
C
and AC  DF.
E
• Be sure to pay attention to the proper notation when naming
parts.
• For instance:
–  ABC   DEF
• By the way, this is called a congruence statement.
» The order of the first triangle is usually done in alphabetical order.
» The order of the second triangle must match up the corresponding angles.
Example 4.1
In the figure above, TJM  PHS. Complete the following statements.
a)
Segment JM  ___________
a)
segment HS
P  ________
b)
T
b)
mM  ________
c)
48o
c)
d)
mP = ________
73o
d)
e)
MT = ________
e)
5 cm
HPS  __________
f)
JTM
f)
•
Yes, the order is important!
Postulate 19:
Side-Side-Side Congruence Postulate
• If three sides of one triangle are congruent to three sides of a
second triangle, then the two triangles are congruent.
– Abbreviated
– SSS
• That means, if
AB  RS , (SIDE)
BC  ST , (SIDE)
and
then
AC  RT , (SIDE)
ABC 
RST .
Postulate 20:
Side-Angle-Side Congruence Postulate
• If two sides and the included angle of one triangle are
congruent to two sides and the included angle of a second
triangle, then the two triangles are congruent.
– Abbreviated
– SAS
• That means, if
RT  UW , (SIDE)
R  U , (ANGLE)
and
RS  UV , (SIDE)
then
RST  UVW .
Example 4.2
It is the same segment, just in two different
triangles. But since it is the same segment,
it has to be congruent. So that makes the
third congruence we need to find the
congruent triangles.
When two lines intersect, they form vertical
angles, and vertical angles are always
congruent. So that makes the third
congruence we need to find the congruent
triangles.
Is there enough information given to prove the triangles are congruent?
If so, state the postulate or theorem that would prove them so.
1.
2.
3.
4.
Yes, SSS
No, SSA does not
guarantee congruent s.
Yes, SAS
No, SSA
does not
guarantee
congruent
s.
Lesson 4.1a Homework
• Lesson 4.1: Day 1 – Congruent Triangles
– p1-2
• Due Tomorrow
Lesson 4.1
Day 2:
More Congruent Triangles
Postulate 21:
Angle-Side-Angle Congruence
• If two angles and the included side of one triangle are
congruent to two angles and the included side of a second
triangle, then the two triangles are congruent.
– Abbreviated
– ASA
• That means, if
A  D, (ANGLE)
AC  DF , (SIDE)
and
then
C  F , (ANGLE)
ABC 
DEF .
Theorem 4.5:
Angle-Angle-Side Congruence
• If two angles and a non-included side of one triangle are
congruent to two angles and the corresponding non-included
side of the second triangle, then the two triangles are
congruent.
– Abbreviated
– AAS
• That means, if
A  D, (ANGLE)
C  F , (ANGLE)
and
BC  EF , (SIDE)
then
ABC 
DEF .
Example 4.3
It is the same segment, just in two different
triangles. But since it is the same segment,
it has to be congruent. So that makes the
third congruence we need to find the
congruent triangles.
When two lines intersect, they form vertical
angles, and vertical angles are always
congruent. So that makes the third
congruence we need to find the congruent
triangles.
Is there enough information given to prove the triangles are congruent?
If so, state the postulate or theorem that would prove them so.
1.
2.
3.
4.
Yes, AAS
Yes, ASA
Yes, AAS
No, there needs to be at least
one pair of congruent sides.
Theorem 4.8:
Hypotenuse-Leg Congruence Theorem
• If the hypotenuse and a leg of a right triangle are congruent to
the hypotenuse and a leg of a second right triangle, then the
two triangles are congruent.
– Abbreviate using
• HL
BC  EF , (HYPOTENUSE)
– It still means, if
with
then
AB  DE , (LEG)
A  D, (RIGHT ANGLE)
ABC 
DEF .
Example 4.4
It is the same segment, just in two different
triangles. But since it is the same segment,
it has to be congruent. So that makes the
third congruence we need to find the
congruent triangles.
Determine if enough information is given to conclude the triangles are congruent using
HL Congruence?
1.
2.
3.
4.
Yes
Yes
Yes
No, because
HL Congruence only
works in right triangles.
Which One Do I Use?…How Can I Tell?
The best way to determine which congruence postulate/theorem
is to identify the number of each part that is marked.
•
If there are more sides marked than
angles, then use one of the following:
– SSS
• If ALL three sides are marked as
congruent pairs.
– SAS
• If ONLY two sides are marked with the
angle IN BETWEEN.
– HL
• Only works in RIGHT TRIANGLES
– Notice the angle is NOT IN BETWEEN
the two sides.
» It looks like SSA.
•
If there are more angles marked than
sides, then use one of the following:
– ASA
• If ANY two angles are marked with the
side IN BETWEEN.
– AAS
• If ONLY two angles are marked along
with a side that is NOT IN BETWEEN.
– Notice, the side must come NEXT to the
same angle that is marked the same
way in both triangles.
Lesson 4.1b Homework
• Lesson 4.1: Day 2 – More Congruent Triangles
– p3-4
• Due Tomorrow
Lesson 4.2
Proving Triangles are Congruent
Lesson 4.2 Objectives
• Create a proof for congruent triangles. (G2.3.1)
• Identify corresponding parts of congruent
triangles. (G2.3.2)
Remembering Proofs
• Do you remember how to write a two-column proof?
• What is the first step?
• Rewrite the problem because…
• That was what was GIVEN to you.
• What should you write in the left-hand column?
– The STATEMENTS you are making as you try to solve the problem.
• What must you show in the right-hand column?
– The REASONS for why you made that statement.
The Understood Properties of Congruence
Property
Definition
Why use this
property?
Reflexive
Symmetric
Transitive
For any segment AB,
If AB  CD,
If AB  CD and CD  EF ,
AB  AB.
then CD  AB.
then AB  EF .
This property allows us
This property is used
to change sides of an
to show that a segment
equal or congruent
is shared between two
sign without losing the
figures.
truth of the statement.
How it’s
identified in a
picture
This property allows us to
conclude that when multiple
segments are congruent to
the same segment, then
they are congruent to each
other.
IF
Usually
in the proof
itself, not in the picture.
AND
THEN
For any angle A, A  A.
Other places
it’s used
If A  B, then B  A.
If A  B and B  C,
then A  C.
Example 4.5
HI  JK
IJ  KH
JH  JH
HIJ 
JKH
Example 4.6
WX  YX
time you are GIVEN a vocabulary word…
Z is the midpoint ofAnyWY
WZ  YZ
XZ  XZ
WXZ  YXZ
Proof Building Tips
•
Here are a few helpful hints to building a proof:
1.
If there is a mark already on the picture, then there should be a step in the proof to
explain the mark.
1.
2.
Those marks should be from the GIVEN, but if not…the reason in the proof would still be
GIVEN.
Any time you add a mark to the picture, you need a step for that it in your proof.
2.
This would be a good time for the REFLEXIVE PROPERTY.
–
3.
Or things like
»
Vertical Angles
»
Midpoint
»
Parallel Line Theorems
»
Transitive Property (MAYBE)
Always be sure the last STATEMENT in the proof is an exact match to what you are
trying to PROVE in the problem.
Example 4.7
Once you have
3 congruencies,
you should have enough
to prove the triangles
are congruent.
1. K  N
1. Given
2. KML  NML
2. Given
3. LM  LM
3. Reflexive Property
4. KML 
NML
4. AAS Congruence
Lesson 4.2 Homework
• Lesson 4.2 – Proving Congruent Triangles
– p5-6
• Due Tomorrow
Lesson 4.3
Similar Triangles
Lesson 4.3 Objectives
• Show triangles are similar using the correct
postulate/theorem. (G2.3.3)
• Solve similar triangles. (G2.3.4)
• Utilize the scale factor and proportions to solve
similar triangles. (G2.3.5)
Ratio
• If a and b are two quantities measured in the same
units, then the ratio of a to b is a/b.
– It can also be written as a:b.
• A ratio is a fraction, so the denominator cannot be zero.
• Ratios should always be written in simplified form.
– 5/10  1/2
Similarity of Polygons
• Two polygons are similar when the following two conditions exist
– Corresponding angles are congruent.
– Corresponding sides are proportional.
• Means that all corresponding sides fit the same ratio.
• Basically we are saying we have two polygons that are the same shape but
different size.
• We use similarity statements to name similar polygons.
– GHIJ ~ KLMN
• You must match the order of the second polygon with that of the first to show
corresponding angles and sides!
Scale Factor
• Remember, polygons will be similar when their
corresponding sides all fit the same ratio.
• That common ratio is called a scale factor.
– We use the variable k to represent the scale factor.
• So k = 3/2 or k = 2/3 , depending on which way you look at it.
» Remember, it’s a ratio!
Postulate 25:
Angle-Angle Similarity Postulate
• If two angles of one triangle are congruent to
two angles of another triangle, then the two
triangles are similar.
Theorem 8.2:
Side-Side-Side Similarity
• If all the corresponding sides of two triangles are
proportional, then the triangles are similar.
– Your job is to verify that all corresponding sides fit the same
exact ratio!
8 4

6 3
Shortest sides
12 4

9 3
16 4

12 3
2nd shortest sides
Longest sides
Theorem 8.3:
Side-Angle-Side Similarity
• If an angle of one triangle is congruent to an angle of a second
triangle and the lengths of the corresponding sides including
these angles are proportional, then the triangles are similar.
– Your task is to verify that two sides fit the same exact ratio and the
angles between those two sides are congruent!
28 7

16 4
SIDE
21 7

12 4
ANGLE
SIDE
Example 4.8
1.
Are the triangles similar?
84 6

14 1
2.
YES,
by SSS
If so, list the congruent angles.
A  H
3.
72 6

12 1
B  G
Also, what is the scale factor?
C  F
k 6
48 6

8 1
Example 4.9
3.
Yes, by
SSS Similarity.
QRS ~ TUV
84 14

30 5
70 14

25 5
42 14

15 5
State if the triangles are similar. If so, write a similarity statement
AND the postulate or theorem that makes them similar.
1.
2.
VA
Yes, by AA.
VA
49 7

14 2
28 7

8 2
Yes, by
SAS Similarity.
LMV ~ UTV
HST ~ HFG
Example 4.10
State if the triangles are similar. If so, write a similarity statement
AND the postulate or theorem that makes them similar.
Corresponding
1.
2.
Angles
Postulate
Reflexive
Property
C
B
A
D
A
E
39
16
40
16
Scale factors must be
equal!
Yes, by AA Similarity
ABD ~ ACE
Not similar
Lesson 4.3 Homework
• Lesson 4.3 – Similar Triangles
– p7-8
• Due Tomorrow
Lesson 5.4
Using Similar Triangles
Lesson 4.4 Objectives
• Identify corresponding parts of congruent
figures.
• Solve similar triangles. (G2.3.4)
• Utilize the scale factor and proportions to solve
similar triangles. (G2.3.5)
Proportion
a
c
=
b
d
• An equation that has two ratios equal to each other is
called a proportion.
– A proportion can be broken down into two parts:
• Extremes
– Identifies the partnership of the numerator of the first ratio and the
denominator of the second ratio.
• Means
– Identifies the partnership of the denominator of the first ratio and
numerator of the second ratio.
Solving Proportions
a
c
=
b
d
ad = bc
• To solve a proportion, you must use the cross product property.
– More commonly referred to as cross-multiplying.
• So multiply the extremes together and set them equal to the
means.
Example 4.11
Solve the following proportions using the Cross Product Property
1. x  10
2. 8  x
3. 4 x  8
4. x  3  15 5. x  7  x  4
7
35
35x  70
x2
17
136
1088  17x
x  64
9
6
4
5
6(4 x)  72
5( x  3)  60
24x  72
5x 15  60
x 3
5x  45
x 9
2
4
4( x  7)  2( x  4)
4x  28  2x  8
2x  28  8
2x  36
x  18
Solving Similar Triangles
• You must use a proportion to solve similar triangles.
• To set-up the proportion it is best to match
corresponding sides in each ratio.
– BE CAREFUL TO SET UP EACH RATIO THE SAME WAY
• So make the top of each ratio represent the small triangle (for
instance) and the bottom of each ratio represent the larger triangle.
Example 4.12
Either way, it
should result
in the same ratio
for similar triangles.
Find the scale factor.
2 14

7 49
Largest sides must
work together.
Or partner the
smallest sides
together IN THE
SAME ORDER.
8 2

28 7
Example 4.13
Find KJ.
28
x

33 42
42x  924
x  22
Notice, each ratio
was made with
corresponding parts in the
SAME ORDER!
Example 4.14
The other ratio
comes from
using the
scale factor.
Solve for x using the given scale factor.
3 x  11 5

42
6
6(3 x  11)  210
18x  66  210
18x  144
x 8
Example 4.15
Find the height, h, of the flagpole.
h 18

5
6
6h  90
h  15 ft
Notice, h is a part of
the large triangle. So be
careful when selecting the
length of another side when
building your
proportion.
Lesson 4.4 Homework
• Lesson 4.4 – Using Similar Triangles
– p9-10
• Due Tomorrow