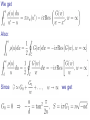* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download ppt - Purdue University
Elementary particle wikipedia , lookup
Coherent states wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Spin (physics) wikipedia , lookup
EPR paradox wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Quantum field theory wikipedia , lookup
Bell's theorem wikipedia , lookup
Renormalization wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Hidden variable theory wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Scale invariance wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Yang–Mills theory wikipedia , lookup
Scalar field theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
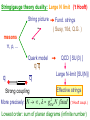
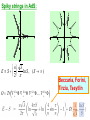
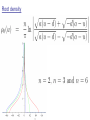
Spiky Strings in the SL(2) Bethe Ansatz M. Kruczenski Purdue University Based on: arXiv:0905.3536 (L. Freyhult, A. Tirziu, M.K.) Quantum Theory and Symmetries 6, 2009 Summary ● Introduction String / gauge theory duality (AdS/CFT) Classical strings and field theory operators: folded strings and twist two operators ● Spiky strings and higher twist operators Classical strings moving in AdS and their field theory interpretation ● Spiky strings in flat space Quantum description. ● Spiky strings in Bethe Ansatz Mode numbers and BA equations at 1-loop ● Solving the BA equations Resolvent ● Conclusions and future work Extending to all loops we a find precise matching with the results from the classical string solutions. String/gauge theory duality: Large N limit (‘t Hooft) String picture Fund. strings ( Susy, 10d, Q.G. ) mesons π, ρ, ... Quark model QCD [ SU(3) ] qq q q Strong coupling Large N-limit [SU(N)] Effective strings 2 More precisely: N , gYM N fixed (‘t Hooft coupl.) Lowest order: sum of planar diagrams (infinite number) AdS/CFT correspondence (Maldacena) Gives a precise example of the relation between strings and gauge theory. Gauge theory String theory N = 4 SYM SU(N) on R4 IIB on AdS5xS5 radius R String states w/ E Aμ , Φi, Ψa Operators w/ conf. dim. gs g ; R / ls ( g 2 YM N , g R 2 YM 2 YM N fixed N) 1/ 4 λ large → string th. λ small → field th. Can we make the map between string and gauge theory precise? Nice idea (Minahan-Zarembo, BMN). Relate to a phys. system, e.g. for strings rotating on S3 › Tr( X X…Y X X Y ) operator mixing matrix H 2 4 | ↑ ↑…↓ ↑ ↑ ↓ conf. of spin chain op. on spin chain J j 1 1 S j S j 1 4 Ferromagnetic Heisenberg model ! For large number of operators becomes classical and can be mapped to the classical string. It is integrable, we can use BA to find all states. Rotation on AdS5 (Gubser, Klebanov, Polyakov) Y Y Y Y Y Y R 2 1 2 2 2 3 2 4 sinh 2 ; [ 3] 2 5 2 6 2 cosh 2 ; t ds cosh dt d sinh d 2 2 2 2 2 2 [ 3] E S ln S , ( S ) θ=ωt O Tr S , x z t Generalization to higher twist operators O[ 2 ] Tr S O[ n ] Tr S / n S / n S / n S / n In flat space such solutions are easily found in conf. gaug x A cos[(n 1) ] A (n 1) cos[ ] y A sin[(n 1) ] A (n 1) sin [ ] Spiky strings in AdS: n E S ln S , ( S ) 2 O Tr S / n S / n S / n S / n Beccaria, Forini, Tirziu, Tseytlin Spiky strings in flat space Quantum case Classical: Quantum: x A cos[(n 1) ] A (n 1) cos[ ] y A sin[(n 1) ] A (n 1) sin [ ] Strings rotating on AdS5, in the field theory side are described by operators with large spin. Operators with large spin in the SL(2) sector Spin chain representation si non-negative integers. Spin Conformal dimension S=s1+…+sL E=L+S+anomalous dim. Bethe Ansatz S particles with various momenta moving in a periodic chain with L sites. At one-loop: We need to find the uk (real numbers) For large spin, namely large number of roots, we can define a continuous distribution of roots with a certain density. It can be generalized to all loops (Beisert, Eden, Staudacher E = S + (n/2) f() ln S Belitsky, Korchemsky, Pasechnik described in detail the L=3 case using Bethe Ansatz. Large spin means large quantum numbers so one can use a semiclassical approach (coherent states). Spiky strings in Bethe Ansatz BA equations Roots are distributed on the real axis between d<0 and a>0. Each root has an associated wave number nw. We choose nw=-1 for u<0 and nw=n-1 for u>0. Solution? i Define d and We get on the cut: Consider z C -i a We get Also: Since we get We also have: Finally, we obtain: Root density We can extend the results to strong coupling using the all-loop BA (BES). We obtain (see Alin’s talk) In perfect agreement with the classical string result. We also get a prediction for the one-loop correction. Conclusions We found the field theory description of the spiky strings in terms of solutions of the BA equations. At strong coupling the result agrees with the classical string result providing a check of our proposal and of the all-loop BA. Future work Relation to more generic solutions by Jevicki-Jin found using the sinh-Gordon model. Relation to elliptic curves description found by Dorey and Losi and Dorey. Semiclassical methods?