* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Rotational Motion
Jerk (physics) wikipedia , lookup
Routhian mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Tensor operator wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Brownian motion wikipedia , lookup
Renormalization group wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Classical mechanics wikipedia , lookup
Old quantum theory wikipedia , lookup
Seismometer wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Centripetal force wikipedia , lookup
Work (physics) wikipedia , lookup
Accretion disk wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Photon polarization wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Angular momentum wikipedia , lookup
Hunting oscillation wikipedia , lookup
Angular momentum operator wikipedia , lookup
Classical central-force problem wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Equations of motion wikipedia , lookup
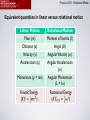
Physics 2015: Rotational Motion Purpose Use the principle of conservation of energy to verify that gravitational potential energy can be converted into rotational kinetic energy and linear kinetic energy in a simple experiment. Use the principle of conservation of momentum to explain transfer of momentum during a collision of rotating bodies. Use the principle of conservation of momentum to explain how changing the shape of a rotating body affects the rotational velocity. Physics 2015: Rotational Motion Equivalent quantities in linear versus rotational motion Linear Motion Rotational Motion Mass (m) Distance (x) Velocity (v) Acceleration (a) Moment of Inertia (I) Angle (Ɵ) Momentum (p = mv) Angular Velocity (ω) Angular Acceleration (α) Angular Momentum (L = Iω) Physics 2015: Rotational Motion Type Force Position Velocity Momentum Linear Motion Rotational Motion Physics 2015: Rotational Motion Activity I: Rotating Bodies and Conservation of Energy Setup: As hanging mass drops, the plate starts to rotate faster and faster. Task: Design an experiment to determine whether total energy is conserved. Important: Take into account all types of energy you can think of that are relevant here. Diagram 2 Physics 2015: Rotational Motion Note that the “Smart Pulley” (circled below) measures its own angular velocity, which is NOT the same as that of the platter. The “Smart Pulley’s” angular velocity and the platter’s angular velocity are related. You need to find this relationship. Physics 2015: Rotational Motion Activity II: Collision Between Rotating Bodies Setup: Main platter rotates, auxiliary platter is dropped on top of main platter Task: Design an experiment to determine whether total angular momentum is conserved. Important: You need to turn the main platter upside down as shown in the diagram. Diagram 3 Physics 2015: Rotational Motion Activity III: The Spinning “Ice Skater” Setup: U-channel placed on top of platter. Movable weights (little carts with wheels) can be pulled Inwards by a thread. Task: Test conservation of angular Momentum as carts are pulled in. Hint: Threads must be routed through holes on the side of the spindle and come out on the top of the spindle, where you can pull on them upwards. Diagram 4