* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Preparing projected entangled pair states on a quantum computer
Particle in a box wikipedia , lookup
Jack Sarfatti wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Scalar field theory wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Quantum dot wikipedia , lookup
Renormalization wikipedia , lookup
Quantum field theory wikipedia , lookup
Delayed choice quantum eraser wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Hydrogen atom wikipedia , lookup
Path integral formulation wikipedia , lookup
Quantum decoherence wikipedia , lookup
Coherent states wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Renormalization group wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Dirac bracket wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Bell test experiments wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Quantum fiction wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Density matrix wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Probability amplitude wikipedia , lookup
Bell's theorem wikipedia , lookup
Quantum computing wikipedia , lookup
History of quantum field theory wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
EPR paradox wikipedia , lookup
Quantum machine learning wikipedia , lookup
Quantum key distribution wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum entanglement wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Quantum group wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Canonical quantum gravity wikipedia , lookup
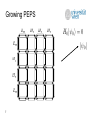
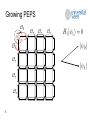
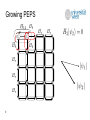
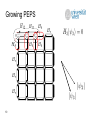
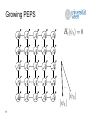
Preparing Projected Entangled Pair States on a Quantum Computer Martin Schwarz, Kristan Temme, Frank Verstraete University of Vienna, Faculty of Physics, Boltzmanngasse 5, 1090 Vienna, Austria Toby Cubitt, David Peréz-García Mathematics and Quantum Information group, Departamento de Analisis Matematico, Facultad de CC Matematicas, Universidad Complutense de Madrid, Plaza de Ciencias 3, Ciudad Universitaria, 28040 Madrid, Spain Phy. Rev. Lett. 108, 110502 (2012), arXiv:1104.1410 Overview • • • • • 2 Some PEPS background Growing PEPS Run-time bound Generalizations Conclusion PEPS properties • Projected entangled-pari states (PEPS) are a natural parameterization of multi-partite quantum states defined on lattices • Conjectured structure of ground states of gapped local Hamiltonians • Proven so by Hastings[1] for 1D case (Matrix Product States) • General PEPS preparation oracles are powerful resources![2] – as powerful as contracting tensor networks or computing their norm – PP-complete, for general PEPS given as classical input Key question raised by Verstraete, Wolf, Peréz-García, Cirac (2006)[3]: Is it possible to prepare PEPS in BQP under mild restrictions? If PEPS generation is hard, what subclass of PEPS are physical? 3 [1] M. Hastings, Journal of Stat. Mech. 2007, P08024 (2007) [2] N. Schuch, M. Wolf, FV, and J.I. Cirac, PRL 98, 140506 (2007) [3] FV, M. Wolf, DPG, and J. Cirac, PRL 96, 220601 (2006) PEPS definition • • • • 4 PEPS are quantum states defined on an arbitrary graph G=(V,E). Edges of G are associated to maximally entangled pairs states providing virtual indices. A tensor A(v) of rank k+1 is associated to each vertex v of degree k mapping k virtual indices to one physical index. PEPS is created by applying the maps A(v) to the virtual indices. Injective PEPS • A PEPS is called injective, iff the map A(v) is left-invertible (after blocking sites), i.e. • Injectivity is a generic property of many interesting states (e.g. 2D AKLT, all lattices, etc. almost always injective) • Each injective PEPS is the unique ground state of a parent Hamiltonian[4] • There is a standard construction[4] for 2-local parent Hamiltonian H = projector onto the complement of the support of each 2-body reduced density matrix of PEPS 5 [4] DPG, FV, J. I. Cirac, and M. M. Wolf, Quant. Inf. Comp 8, 0650 (2008) Growing PEPS Key idea for preparing injective PEPS: 1. prepare a set of entangled pair states, one for each edge 2. construct parent Hamiltonian with entangled pairs as groundstate • treat “virtual“ PEPS indices as physical indices as well 3. grow the PEPS by growing the parent Hamiltonian, vertex by vertex 1. update parent Hamiltonian edge and vertex terms 2. add Hamiltonian term to restrict to the physical subspace with energy penalty larger than spectral gap D 1. project onto unique ground state vector of updated Hamiltonian – This step is probabilistic and requires some more work… 4. final ground state is the PEPS we want to prepare 6 Growing PEPS 7 Growing PEPS 8 Growing PEPS 9 Growing PEPS 10 Growing PEPS … 11 Projecting on next ground state • • • • • • Projection onto the next ground state is performed using Phase Estimation[5] We perform a binary measurement on the energy register (zero or non-zero) If the outcome is zero, we have perpared the desired ground state Else, we undo the measurement using the well-known Marriot-Watrous trick[6] and re-try, either starting from the original state or an orthogonal one By Jordan´s Lemma, analysis reduces to a single 2x2 block, i.e. 2D subspace Transition may also be effected adiabatically[7] (doesn‘t generalize to G-inj. case) unique GS of Ht+1 unique GS of Ht 12 [5] M. Nielsen, I. Chuang. Quant. Comp. and Quant. Inf., Cambridge Univ. Press. (2000) [6] C. Marriot, J. Watrous, Comput. Complex. 14, pp. 122-152. (2003) [7] D. Aharonov, A. Ta-Shma, SIAM J. Comput. Vol. 37, No. 1, pp. 47-82, (2007) Bounding the run-time • We need a lower bound for the transition probability • Let • Then, using the PEPS structure, we show that for each injective PEPS • • • Let k=max(k(A(v))) be the max. condition number over all PEPS projectors A(v) Let D=min(D(Ht)) be the smallest spectral gap over all Ht generated Then the algorithm produces PEPS p with probability at least 1-e in time 13 be the condition number of matrix A Generalization • The algorithm generalizes to G-injective PEPS[8], where symmetry group G is acting on virtual indices and A(v) is left-invertible on the Ginvariant subspace. A PEPS is called G-isometric, if all A(v)´s are isometries. • Problem: A(v)´s not injective parent Hamiltonian has degenerate ground space! How can we undo failed projections which are not rank-1? 14 [8] N. Schuch, J.I. Cirac, DPG, Annals of Physics, Volume 325, Issue 10 (2010) Growing G-injective PEPS • Generalization of the basic algorithm – A related G-isometric PEPS is prepared deterministically by known methods[9,10] to enter the G-invariant subspace first – The G-isometric PEPS is then transformed into the G-injective PEPS as before, maintaining the G-invariant subspace – To undo measurements, we crucially use the PEPS structure and the fact that A(v) is invertible on the the G-invariant subspace to show that in fact we can proceed as before! • Same run-time bound as basic algorithm. • Examples of G-isometric PEPS being prepared initially: – G=Z1: – G=Z2: (trivial): product of entangled pairs (same as before) well-known toric code state • The class of G-injective PEPS includes many physically interesting states with topologically order, such as quantum double models, etc. 15 [9] M. Aguado, G. Vidal, Phys. Rev. Lett. 100, 070404 (2008) [10] FV, M. M. Wolf, and J. I. Cirac. Nature Physics, 5:633–636 (2009) Conclusion • We have shown how to efficiently (in BQP) prepare well-conditioned injective PEPS on a quantum computer with high probability. • We have exploited the PEPS structure to construct a sequence of parent Hamiltonians with an induced sequence of unique ground states with lowerbounded overlap, and we have shown how to move through this sequence efficiently to produce the final PEPS. • The result generalizes to G-injective PEPS yielding the same run-time bound of (with k restricted to the G-invariant subspace) • Future directions: 16 – implement quadratic speedup in k by using Quantum Rejection Sampling[11] – can we solve interesting computational problems in this PEPS framework faster?[12] [11] M. Ozols, M. Roetteler, J. Roland, arXiv:1103.2774 (2011) [12] I. Arad, Z. Landau, SIAM Journal on Computing 39, 3089 (2010) References 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 17 M. Hastings, Journal of Statistical Mechanics: Theory and Experiment 2007, P08024 (2007) N. Schuch, M. Wolf, F. Verstraete, and J.I. Cirac, PRL 98, 140506 (2007) F. Verstraete, M. Wolf, D. Perez-Garcia, and J. Cirac, PRL 96, 220601 (2006) D. Perez-Garcia, F. Verstraete, J. I. Cirac, and M. M. Wolf, Quant. Inf. Comp 8, 0650 (2008) D. Aharonov, A. Ta-Shma, SIAM J. Comput. Vol. 37, No. 1, pp. 47-82, (2007) C. Marriot, J. Watrous, Comput. Complex. 14, pp. 122-152. (2003) M. A. Nielsen, I. L. Chuang. Quantum Comp. and Quantum Inf., Cambridge Univ. Press. (2000) N. Schuch, J.I. Cirac, D. Peréz-García, Annals of Physics, Volume 325, Issue 10 (2010) M. Aguado, G. Vidal, Phys. Rev. Lett. 100, 070404 (2008) F. Verstraete, M. M. Wolf, and J. I. Cirac. Nature Physics, 5:633–636 (2009) M. Ozols, M. Roetteler, J. Roland, Quantum rejection sampling, arXiv:1103.2774 (2011) I. Arad, Z. Landau, SIAM Journal on Computing 39, 3089 (2010)