* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 1 Introduction: Physical Quantities, Units and Mathematical
Field (physics) wikipedia , lookup
Anti-gravity wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Nuclear physics wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Magnetic monopole wikipedia , lookup
Fundamental interaction wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Elementary particle wikipedia , lookup
Electromagnetism wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Maxwell's equations wikipedia , lookup
Atomic nucleus wikipedia , lookup
Lorentz force wikipedia , lookup
Atomic theory wikipedia , lookup
149
Chapter 22 Electric charge
22-1 Electromagnetism
The early Greek philosophers knew that if you rubbed a piece of amber, it would
attract bits of straw. The Greeks also recorded the observation that some naturally
occurring “stones” would attract iron.
The sciences of electricity and magnetism developed separately for centuries – until
1820 when Oersted found an electric current in a wire can deflect a magnetic compass
needle.
The new science of electromagnetism (the combination of electrical and magnetic
phenomena) was developed further by research workers in many countries – Michael
Faraday and later James Clerk Maxwell.
22-2 Electric charge
An intrinsic characteristic of the fundamental particles making up those objects.
Two kinds: positive and negative
Electrical isolation: for example, a charged rod is suspended from a thread so that its
charge cannot change.
Charges with the same electrical sign repel each other, and charges with opposite
electrical signs attract each other.
22-3
Conductors: some of the negative charge can move rather freely.
Insulators (nonconductors): none of the charge can move freely.
Ground: setting up a pathway of conductors between an object and Earth’s surface.
Discharge: neutralizing the object by eliminating an unbalanced positive or negative
charge.
Electrons: negatively charged
Protons: positively charged
Neutrons: electrically neutral
In atoms, for example copper, some of their outermost electrons do not remain
attached to the individual atoms but become free to more within the solid. These mobile
electrons are called conduction electrons.
150
Demonstration of the mobility of charge
conductor.
Induced charge: some of its positive and
negative charges have been separated.
Semiconductors are materials that are
intermediate between conductors and
insulators.
Superconductors: no resistance to the
movement of charge.
in a
151
The Si unit of charge is the coulomb: one coulomb is the amount of charge that is
transferred through the cross section of a wire in 1 second when there is a current of 1
ampere in the wire.
152
If excess charge is placed on a spherical shell that is made of conducting material, the
excess charge spreads uniformly over the (external) surface.
153
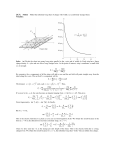
Six fixed charged particles where a=2.0cm and Θ=30ο.All six particles have the same magnitude of
charge, q=3.0*10-6C. What is the net electrostatic force F, acting on q, due to the other charges?
vfd
a
2a
a
Θ
a
a
154
1
F 12 = F 14 =
q1 q 2
4πε 0 (2a) 2
F 13 = F 15 = F 16 =
1
q1 q3
4πε 0
a2
F 1 = F 16 - 2F 13 sin θ
=
1
4πε 0
q1 q 6
a
2
-
2
q1 q3
4πε 0
a2
q 1 = q 3 and θ = 30°
F 1 =0
sin θ
155
156
157
Quarks, the constituent particles of protons and neutrons, have charges of ±e/3 or ±2e/3,
but they apparently cannot be detected individually. For this and for historical reasons,
We do not take their charges to be the elementary charge.
An electrically neutral penny, of mass m=3.11g, contains equal amounts of positive and
negative charge.
(a) Assuming that the penny is made entirely of copper, what is the magnitude q of the
total positive (or negative) charge in the coin?
(b) Suppose that the positive charge and the negative charge in a penny could be
concentrated into two separate bundles, loom apart. What attractive force would act on
each bundle?
Sol:
(a) Z = 29 N = N A m/M
q = NZe = 137000C
(b) F =
q2
16
=1.69X10 (N)
2
4πε 0 r
1
large!!
158
159
160
Exercises:9,20,29,39
161
Chater23
Question: If we move q1 toward q2, does the electric field q2, and thus the force acting onq2, change
immediately?
Answer: No. Electromagnetic wave at the speed of light C.
162
The electric field exists independently of the test charge. (We assume that in our defining procedure, the
presence of the test charge does not affect the charge distribution on the charged object.)
Lines of force: electric field lines. A good way to visualize patterns in electric fields.
163
Electric field lines extend away from positive charge and toward negative
charge.
164
165
166
167
168
The nucleus of a uranium atom has a radius R of 6.8fm. Assuming that the positive charge of the nucleus
is distributed uniformly, determine the electric field at a point on the surface of the nucleus due to that
charge.
Sol: Z=92
E=
1
Ze
=2.9X1021(N/C)
4πε 0 R 2
169
170
(Can never find q and d separately !)
171
172
173
174
175
176
Tactics: 1. the element ds, for instance
2. dq=λds
K
3. d E = ?
4. Symmetry
177
178
A disk has a surface charge density σ of +5.3μC/m2 on its upper face. (This is a reasonable value for the
surface charge density on the photo sensitive cylinder of a photo copying machine, incidentally.)
(a) What is the electric field at the surface of the disk?
E=
σ
= 3.0 X 10 5 N / C
2ε 0
(b) Using the binomial theorem, find an expression for the electric field at a point of the central axis far
from the disk.
(1 + x) n = 1 +
Z
Z 2 + R2
(1 +
2
=
R −1 / 2
)
Z2
First order
n
n(n − 1) 2
x+
x + ...
1!
2!
Z
Z (1 +
R2
)
Z2
= (1 +
R 2 −1 / 2
)
Z2
1
1 1
− (− − 1) 4
2
R
R
= 1+ 2 2 + 2 2
+ ....
1! Z
2!
Z4
−
R 2
1 −
2Z 2
179
E=
σ
R2
1 q
[1 − (1 − 1 −
)] =
2
2ε 0
4πε 0 Z 2
2Z
180
181
182
183
184
Exercises: 19,30,33,51
185
Chapter 24
A new formation of coulomb’s law – Gauss’ law
Gaussian surface: a hypothetical closed surface central to Gauss’ law
Description: Gauss’ law relates the electric fields at points on a closed Gaussian surface
and the net charge enclosed by that surface.
Φ: The volume flow rate, volume per unit time.
υ: Uniform velocity
A: square loop of area
186
187
188
189
190
191
First thought: repulsionÆ reasonable.
K
Inside the conductor, E must be zero. If this were not so, the field would exert forces on
the conduction electrons, causing an electric current.
Important theorem: E=0 inside a conductor.
192
(External electric field for conducting surface)
193
194
195
196
197
edge effect of fringing.
198
199
200
201
Cf. Gravitation
Results: E ∝
{
r-2
r
Exercises:27,35,52,53
,
r≥ R
, r≤ R
uniformly distributed
202
Chapter 25
Electrostatic force is a conservative forceÆ we can assign an electric potential energy U
to the system.
203
204
Equipotential surfaces: a surface that all adjacent points have the same electric potential.
205
206
207
208
(a) What is the electric potential V at a distance r=2.12x10-10m from the nucleus of a
hydrogen atom?
(b) What is the electric potential energy U in electron-volts of an electron at the given
distance from the nucleus?
(c) If the electron moves closer to the proton, does the electric potential energy increase
or decrease?
Sol:
(a) V =
e (8.99 X 10 9 )(1.60 x10 −19 )
=
= 6.78V
4πε 0 r
2.12 X 10 −10
1
(b)U=qv=(-1.60X10-19)(6.78)=-6.78eV
(c) Decreases V=
n
∑Vi =
i =1
1
e n qi
∑ (n point charge)
4πε 0 r i =1 ri
209
210
211
212
213
214
215
The potential at the center of a uniformly charged circular disk of radius R=3.5cm is V 0= 550V
(a) What is the total charge q on the disk?
(b) What is the potential at a point on the axis of the disk a distance Z=5.0R from the center of the disk?
Sol:
(a)Z=0, V 0 =
2ε V
σR
Æσ = 0 0
R
2ε 0
q= σ (πR 2 ) = 2πε 0 RV0 = 1.1nC
(b)Z=5.0RÆV=
σ
( (5.0r ) 2 + R 2 − 5.0 R) = 54V
2ε 0
216
217
218
219
Exercises:24,41,53