* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter S23
History of quantum field theory wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Standard Model wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Elementary particle wikipedia , lookup
Magnetic monopole wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Speed of gravity wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Fundamental interaction wikipedia , lookup
Electromagnetism wikipedia , lookup
Maxwell's equations wikipedia , lookup
Field (physics) wikipedia , lookup
Lorentz force wikipedia , lookup
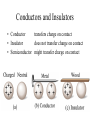
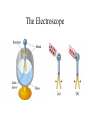
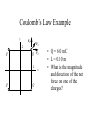
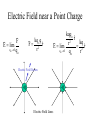
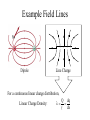
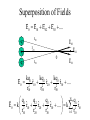
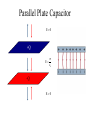
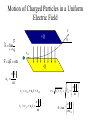
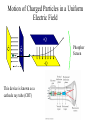
Chapter 23 Electric Charge and Electric Fields • What is a field? • Why have them? • What causes fields? Field Type gravity electric magnetic Caused By mass charge moving charge Electric Charge • Types: – Positive • Glass rubbed with silk • Missing electrons – Negative • Rubber/Plastic rubbed with fur • Extra electrons • Arbitrary choice – convention attributed to ? • Units: amount of charge is measured in [Coulombs] • Empirical Observations: – Like charges repel – Unlike charges attract Charge in the Atom • • • • Protons (+) Electrons (-) Ions Polar Molecules Charge Properties • Conservation – Charge is not created or destroyed, only transferred. – The net amount of electric charge produced in any process is zero. • Quantization – The smallest unit of charge is that on an electron or proton. (e = 1.6 x 10-19 C) • It is impossible to have less charge than this • It is possible to have integer multiples of this charge Q Ne Conductors and Insulators • Conductor transfers charge on contact • Insulator does not transfer charge on contact • Semiconductor might transfer charge on contact Charge Transfer Processes • Conduction • Polarization • Induction The Electroscope Coulomb’s Law • Empirical Observations F q1q 2 1 F 2 r Direction of the force is along the line joining the two charges • Formal Statement kq1q 2 F12 2 rˆ21 r21 Active Figure 23.7 (SLIDESHOW MODE ONLY) Coulomb’s Law Example • What is the magnitude of the electric force of attraction between an iron nucleus (q=+26e) and its innermost electron if the distance between them is 1.5 x 10-12 m Hydrogen Atom Example • The electrical force between the electron and proton is found from Coulomb’s law – Fe = keq1q2 / r2 = 8.2 x 108 N • This can be compared to the gravitational force between the electron and the proton – Fg = Gmemp / r2 = 3.6 x 10-47 N Subscript Convention kq1q 2 F12 2 rˆ21 r21 F12 r̂21 +q2 +q1 r21 F12 force on charge q1 due to charge q2 r21 distance from charge q2 to charge q1 r̂21 unit vector oriented from charge q2 to charge q1 More Coulomb’s Law kq1q 2 F12 2 rˆ21 r21 r̂21 F12 r̂21 r21 r21 +q2 r21 +q1 r21 r21 Coulomb’s constant: permittivity of free space: Charge polarity: 2 2 N m N m 1 9 k 8.988x109 9.0x10 2 C2 C 4o 2 1 C o 8.85x1012 4k N m2 Same sign Opposite sign Force is right Force is Left Electrostatics --- Charges must be at rest! Superposition of Forces F0 F01 F02 F03 .... +Q1 +Q2 +Q3 r10 r20 r30 F03 F02 +Q0 F01 kq 0 q1 kq 0q 2 kq 0q 3 F0 2 rˆ10 2 rˆ20 2 rˆ30 .... r10 r20 r30 N q1 q3 q2 qi F0 kq0 2 rˆ10 2 rˆ20 2 rˆ30 .... kq 0 2 rˆi0 r20 r30 i 1 ri0 r10 Coulomb’s Law Example y + Q F1 L F3 + Q F2 L Q Q + + x • Q = 6.0 mC • L = 0.10 m • What is the magnitude and direction of the net force on one of the charges? Zero Resultant Force, Example • Where is the resultant force equal to zero? – The magnitudes of the individual forces will be equal – Directions will be opposite • Will result in a quadratic • Choose the root that gives the forces in opposite directions Electrical Force with Other Forces, Example • The spheres are in equilibrium • Since they are separated, they exert a repulsive force on each other – Charges are like charges • Proceed as usual with equilibrium problems, noting one force is an electrical force Electrical Force with Other Forces, Example cont. • The free body diagram includes the components of the tension, the electrical force, and the weight • Solve for |q| • You cannot determine the sign of q, only that they both have same sign The Electric Field • Charge particles create forces on each other without ever coming into contact. » “action at a distance” • A charge creates in space the ability to exert a force on a second very small charge. This ability exists even if the second charge is not present. • We call this ability to exert a force at a distance a “field” • In general, a field is defined: Force Why in the limit? Field lim test quantity 0 test quantity • The Electric Field is then: F N E lim C q 0 q Electric Field near a Point Charge kq o q F 2 rˆ r F E lim qo 0 q o kqq o r̂ 2 kq r E lim 2 rˆ q o 0 qo r Electric Field Vectors -Q +Q Electric Field Lines Active Figure 23.13 (SLIDESHOW MODE ONLY) Rules for Drawing Field Lines • The electric field, E , is tangent to the field lines. • The number of lines leaving/entering a charge is proportional to the charge. • The number of lines passing through a unit area normal to the lines is proportional to the strength of the field in that region. # of electric field lines E Area • Field lines must begin on positive charges (or from infinity) and end on negative charges (or at infinity). The test charge is positive by convention. • No two field lines can cross. Electric Field Lines, General • The density of lines through surface A is greater than through surface B • The magnitude of the electric field is greater on surface A than B • The lines at different locations point in different directions – This indicates the field is non-uniform Example Field Lines + Dipole + + + Line Charge For a continuous linear charge distribution, Linear Charge Density: + Q dq dx Active Figure 23.24 (SLIDESHOW MODE ONLY) More Field Lines Q dq A dA Surface Charge Density: Volume Charge Density: Q dq V dV Superposition of Fields E0 E01 E02 E03 .... +q1 +q2 +q3 r10 E03 E02 r20 r30 0 E 01 kq 3 kq1 kq 2 E 0 2 rˆ10 2 rˆ20 2 rˆ30 .... r10 r20 r30 N q1 q3 q2 qi E0 k 2 rˆ10 2 rˆ20 2 rˆ30 .... k 2 rˆi0 r20 r30 i 1 ri0 r10 Superposition Example • Find the electric field due to q1, E1 • Find the electric field due to q2, E2 • E = E1 + E2 – Remember, the fields add as vectors – The direction of the individual fields is the direction of the force on a positive test charge Electric Field of a Dipole (ex. 23.6) E E E E kq E E y a 2 2 E y E E x E x 2E cos -q 2a p p 2aQ +q kq E2 2 2 y a y 2a a y a 2 2 kp E y a 2 kp y3 2 3 2 P23.19 Three point charges are arranged as shown in Figure P23.19. (a) Find the vector electric field that the 6.00-nC and –3.00-nC charges together create at the origin. (b) (b) Find the vector force on the 5.00-nC charge. Figure P23.19 P23.52 Three point charges are aligned along the x axis as shown in Figure P23.52. Find the electric field at (a) the position (2.00, 0) and (b) the position (0, 2.00). Figure P23.52 FIG. P23.52(a) E1 keq 2 r 8.99 10 ˆ r 9 N m 2 C 2 4.00 109 C 2.50 m 2 iˆ 5.75ˆ iN C E2 keq 2 r 8.99 10 ˆ r 9 8.99 10 9 E3 N m 2 N m 2 C 2 5.00 109 C 2.00 m 2 C 2 3.00 109 C 1.20 m 2 ER E1 E2 E3 24.2 N C E1 E2 E3 keq iˆ 11.2 N iˆ 18.7 N ˆ C i in +x direction. 2 ˆ 0.970ˆ ˆ 8.46 N C 0.243i r j 2 ˆ 11.2 N C ˆ r j r keq r keq r2 ˆ 5.81 N r ˆ+0.928ˆ C 0.371i j Ex E1x E3x 4.21ˆ iN C ER 9.42 N C ˆ C i Ey E1y E2y E3y 8.43ˆ jN C 63.4 above x axis P23.19 (a) E1 E2 ke q1 r12 ke q2 r22 8.99 10 3.00 10 8.99 10 6.00 10 9 9 ˆ j 0.100 2 9 9 ˆ i 0.300 2 ˆj 2.70 10 3 N C ˆ j iˆ 5.99 10 ˆ N C i 2 ˆ 2.70 103 N C ˆ E E 2 E1 5.99 102 N C i j (b) ˆ 2 700ˆ F qE 5.00 109 C 599i j N C ˆ 13.5 106 ˆ F 3.00 106 i j N 3.00iˆ 13.5ˆj N Continuous Charge Distributions +Q1 +Q2 +Q3 kq E 0 2 rˆ r kdq dE 0 2 rˆ r Single charge Single piece of a charge distribution r10 E03 E02 r20 0 r30 E 01 + + + + dq dE0 0 N qi E0 k 2 rˆi0 i 1 ri0 dq E0 k rˆ 2 r all charge Discrete charges Continuous charge distribution Finding dq kdq dE 2 rˆ r Line charge Q dq dx Surface charge Q dq A dA Volume charge Q dq V dV Cartesian Polar dq dx dq Rd dq dxdy dq rdrd dq dxdydz dq rdrddz dq r 2 sin drdd Example – Infinitely Long Line of Charge + + kdq dE 2 rˆ r dq dy dy r x y 2 2 y-components cancel by symmetry 2 y + + + + dEx x dE y dE + dE x kdq cos 2 r k dy x dE 2 x y2 x 2 y2 + E kx dy x 2 y 3 2 2 2 2k kx 2 x x Example – Charged Ring (ex 23.8) d + a r x a 2 + 2 y-components cancel by symmetry 2 + + kdq dE 2 rˆ r dq ds ad dEx x + + dE x k ad x dE 2 x a2 x2 a2 dE dE y kdq cos 2 r + E 2 kxa x 2 a d 3 2 2 0 kxa x 2 a 3 2 2 2 kQx x 2 a 3 2 2 Check a Limiting Case E kQx x 2 R 3 2 2 x R When: The charged ring must look like a point source. E kQx 2 x R 3 2 2 kQx 0 2 R 2 x 1 2 x 3 2 kQx kQ 2 3 x x Uniformly Charged Disk (ex. 23.9) E R kQx x 2 r 3 2 2 r x dE dE kxdq x 2 r 3 2 2 dq dA rdrd 2rdr dE kx2rdr x 2 r R E 3 2 2 0 kx2rdr x 2 r 3 2 2 R kx 0 x2 R2 2rdr x 2 r 3 2 2 kx du x u 2 3 2 x2 R2 x2 R2 kx x2 3 2 u du kx u 1 2 1 2 1 1 x 2kx k2 1 2 2 2 2 2 x R x x R x2 Binomial Expansion Theorem 1 x x 1 n n n 1 2 1 nx x ... 2! Quadratic terms and higher are small 1 x n 1 nx Two Important Limiting Cases R x Large Charged Plate: R r x dE x 1 E k2 1 k 2 2 2 2 4o 2o x R Very Far From the Charged Plate: x x E k2 1 k 2 1 2 2 x R R2 x 1 2 x x R 1 2 2 k2 1 1 R x2 1 R 2 1 R 2 kR 2 kQ k2 1 1 k2 2 2 2 2 x x 2 x 2 x Parallel Plate Capacitor E0 +Q E 2 o E o -Q E0 Motion of Charged Particles in a Uniform Electric Field F q 0 q E lim F qE ma qE a m +Q -Q v2 v02 2a x x 0 -e x v x 2a x x 2 eE m x Example • A proton accelerates from rest in a uniform electric field of 500 N/C. At some time later, its speed is 2.50 x 106 m/s. +Q -Q – Find the acceleration of the proton. – How long does it take for the proton to reach this speed? – How far has it moved in this time? – What is the kinetic energy? x e Motion of Charged Particles in a Uniform Electric Field v +Q F E lim q 0 q F qE ma vx0 -e -Q ay eE m e E t 2 2 2 v vx vy vx0 m v x v x0 a x t v x0 v y v y0 a y t eE m t eE t tan mv x0 1 2 Active Figure 23.26 (SLIDESHOW MODE ONLY) Motion of Charged Particles in a Uniform Electric Field +Q +Q -Q Phosphor Screen -e -e x This device is known as a cathode ray tube (CRT) -Q Summary Point Charges: Coulomb’s Law Electric Field kq1q 2 F12 2 rˆ21 r21 F qo 0 q o E lim These can be used to find the fields in the vicinity of continuous charge distributions: + + + + Line of Charge: Charged Plate: R r x dE 2k E x E 2 o Dipole: p kp E + r a 2 2 3 2