Download Improper Fraction

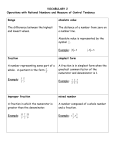
Chapter 2
Fractions
Part 3
Day…..
1) Recipe Magic
2) Models
3) Multistep Story Problems
4) End of Unit Assessment
Day 1
Vocabulary
Dividend-
The number being divided in a division equation. (inside or 1st number)
Divisor- The number doing the dividing in a division equation. (outside or 2nd number)
Equivalent- equal or the same
Fraction- a number that represents part of a whole or part of a set
Greatest Common Factor- the greatest of the common factors of two or more numbers
Improper Fraction- a fraction with a numerator that is greater than or equal to the
denominator
Mixed Number- a number that has a whole number part and a fraction part
Product- the answer to a multiplication equation
Quotient- the answer to a division equation
Reciprocal – two numbers with a product of 1 (flipped upside down)
Scaling- to increase or decrease a ratio
Simplest Form- a fraction in which the GCF of the numerator and denominator is 1
Test Critiques
Please take out a blue ink pen and
your grade assessment.
Today's Standard
Interpret and compute quotients of fractions, and solve
word problems involving division of fractions by fractions,
e.g., by using visual fraction models and equations to
represent the problem. For example, create a story context
for (2/3) ÷ (3/4) and use a visual fraction model to show
the quotient; use the relationship between multiplication
and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4
of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much
chocolate will each person get if 3 people share 1/2 lb of
chocolate equally? How many 3/4-cup servings are in 2/3 of
a cup of yogurt? How wide is a rectangular strip of land
with length 3/4 mi and area 1/2 square mi?
Recipe Magic
Wrap it Up
• Review
• Questions
• Station Work
Day 2
Bell Work
Create a story problem for
6÷¼=
Illustrate the solution
Vocabulary
Dividend-
The number being divided in a division equation. (inside or 1st number)
Divisor- The number doing the dividing in a division equation. (outside or 2nd number)
Equivalent- equal or the same
Fraction- a number that represents part of a whole or part of a set
Greatest Common Factor- the greatest of the common factors of two or more numbers
Improper Fraction- a fraction with a numerator that is greater than or equal to the
denominator
Mixed Number- a number that has a whole number part and a fraction part
Product- the answer to a multiplication equation
Quotient- the answer to a division equation
Reciprocal – two numbers with a product of 1 (flipped upside down)
Scaling- to increase or decrease a ratio
Simplest Form- a fraction in which the GCF of the numerator and denominator is 1
Today's Standard
Interpret and compute quotients of fractions, and solve
word problems involving division of fractions by fractions,
e.g., by using visual fraction models and equations to
represent the problem. For example, create a story context
for (2/3) ÷ (3/4) and use a visual fraction model to show
the quotient; use the relationship between multiplication
and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4
of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much
chocolate will each person get if 3 people share 1/2 lb of
chocolate equally? How many 3/4-cup servings are in 2/3 of
a cup of yogurt? How wide is a rectangular strip of land
with length 3/4 mi and area 1/2 square mi?
Fraction Models
Essential Understandings: Fractions are numbers used to represent
part of a whole or part of a set.
•You can show/solve fraction equations using models.
Example: ¼ divided by ½
But first, you must know how to model different types of
fractions.
•You can model a part of a whole by using a single figure.
Example:
•You can model part of a set using multiple figures.
Example:
Modeling Fraction Equations
Essential Understandings:
Fractions equation models can be used to solve/prove…
•Addition Equations
Example:
•Subtraction Equations
Example:
•Multiplication Equations
Example:
•Division Equations
Example:
Division Models
Essential Understanding:
•Double bar graphs/ fraction strips are an easy way to illustrate fraction equations involving division.
To do this:
• Begin by drawing two bars of equal length, one above the other.
•The top bar will represent the dividend and the bottom bar will represent the divisor.
•Remember to draw the missing portions of wholes, if the dividend is a proper fraction.
Example:
•Now, divide both bars into equal sized parts to represent any wholes in your dividend. If you dividend is a
fraction the entire bar will represent 1 whole.
Example:
•Next, Divide the wholes in the top bar, to represent the denominator of the dividend.
•Then, shade the specified fraction.
Example:
•Now, divide the wholes of the bottom bar to represent the denominator of the divisor.
Example:
•Finally, use the numerator of the divisor to determine how many parts per group need to be circled.
•The number of groups you can create is the answer to the equations.
•Don’t forget to account for any unfinished groups.
Example:
Types of Division Models
• Double Bar / Fraction Strips
Example:
• Double Number Line
Example:
• Picture Models
Example:
Watch This
• http://learnzillion.com/lessons/212-multiplyfractions-by-whole-numbers-using-bar-models
• http://learnzillion.com/lessons/199-dividewhole-numbers-by-unit-fractions-using-visualmodels
• http://learnzillion.com/lessons/1383-solveword-problems-involving-division-of-mixednumbers-and-fractions-using-picture-models
Wrap it Up
• Review
• Questions
• Station Work
Day 3
Bell Work
Create fraction models to illustrate the
following equations.
① ½ of 8 =
② 8÷½=
③ ½÷8=
Explain the differences and similarities.
Vocabulary
Dividend-
The number being divided in a division equation. (inside or 1st number)
Divisor- The number doing the dividing in a division equation. (outside or 2nd number)
Equivalent- equal or the same
Fraction- a number that represents part of a whole or part of a set
Greatest Common Factor- the greatest of the common factors of two or more numbers
Improper Fraction- a fraction with a numerator that is greater than or equal to the
denominator
Mixed Number- a number that has a whole number part and a fraction part
Product- the answer to a multiplication equation
Quotient- the answer to a division equation
Reciprocal – two numbers with a product of 1 (flipped upside down)
Scaling- to increase or decrease a ratio
Simplest Form- a fraction in which the GCF of the numerator and denominator is 1
Today's Standard
Interpret and compute quotients of fractions, and solve
word problems involving division of fractions by fractions,
e.g., by using visual fraction models and equations to
represent the problem. For example, create a story context
for (2/3) ÷ (3/4) and use a visual fraction model to show
the quotient; use the relationship between multiplication
and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4
of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much
chocolate will each person get if 3 people share 1/2 lb of
chocolate equally? How many 3/4-cup servings are in 2/3 of
a cup of yogurt? How wide is a rectangular strip of land
with length 3/4 mi and area 1/2 square mi?
Story Problems
Essential Understanding:
To solve multistep word problems, easily, follow this procedure.
1. Read and visualize the problem.
2. Illustrate what you have visualized .
3. Find key vocabulary that helps you decide what operations to use.
(Hint: In multistep problems, you will notice more than one)
4. Write down what you know and questions you need to answer.
5. Determine the order of events (what has to happen first? What
should be the final outcome?).
6. Write equations using the determined operations.
7. Determine if your equations makes sense.
8. Solve equations in order, carrying information over as necessary.
9. Determine if your answer makes sense.
10. Check or Revise, as needed.
Wrap it Up
• Review
• Questions
• Station Work
Day 4
Bell Work
Taylor has cow pasture that has an area of
300yd2. The length of his pasture is 12 ½ yd2.
What is the width?
He wants to build a barn that covers 1/5 of
the pasture. How much pasture will be left
for the cows to graze?
Vocabulary
Dividend-
The number being divided in a division equation. (inside or 1st number)
Divisor- The number doing the dividing in a division equation. (outside or 2nd number)
Equivalent- equal or the same
Fraction- a number that represents part of a whole or part of a set
Greatest Common Factor- the greatest of the common factors of two or more numbers
Improper Fraction- a fraction with a numerator that is greater than or equal to the
denominator
Mixed Number- a number that has a whole number part and a fraction part
Product- the answer to a multiplication equation
Quotient- the answer to a division equation
Reciprocal – two numbers with a product of 1 (flipped upside down)
Scaling- to increase or decrease a ratio
Simplest Form- a fraction in which the GCF of the numerator and denominator is 1
Today's Standard
Interpret and compute quotients of fractions, and solve
word problems involving division of fractions by fractions,
e.g., by using visual fraction models and equations to
represent the problem. For example, create a story context
for (2/3) ÷ (3/4) and use a visual fraction model to show
the quotient; use the relationship between multiplication
and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4
of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much
chocolate will each person get if 3 people share 1/2 lb of
chocolate equally? How many 3/4-cup servings are in 2/3 of
a cup of yogurt? How wide is a rectangular strip of land
with length 3/4 mi and area 1/2 square mi?
Equivalent Equations
Essential Understanding:
You can create equivalent equations for the division of fractions using
the following methods.
1. Mixed Numbers and Improper Fractions
2. Scaling
3. Keep Change Flip
4. Commutative Property
5. Common Denominators
6. One Step Equations
7. Using Variables
Exit Ticket
Create a KWL chart
for Chapter 1 - Decimals
Know
Want to Know
What I Learned
Wrap it Up
• Review
• Questions
• Station Work