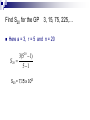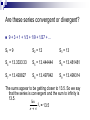Download Series

Series
For the arithmetic series
a + (a + d) + (a + 2d) +…
the sum of n terms is given by
n
Sn = 2 [ 2a + (n – 1) d ]
Or
n
Sn = 2 (t1 + tn)
Find S22 for the AP, 3, 8, 13, …

S22 = 22 [ 2a + ( 22 – 1) d ]
2

For this AP, a = 3 and d = 5

S22 = 22 [ 2 x 3 + 21 x 5 ]
2
= 11 [ 6 + 105 ]
= 11 x 111
S22 = 1221
Find the sum of the AP 7, 11, 15, …, 203.

Here a = 7 and d = 4, but in order to apply the formula for summing
the series, we need to know n.

tn
203
196
49
50




=
=
=
=
=
a + (n - 1) d
7 + (n – 1) 4
4 (n – 1)
n–1
(dividing by 4)
n
So 203 is the 50th term
Now find S50. Use Sn =
50
(7 + 203)
2

S50 =

S50 = 25 x 210

S50 = 5250
n
(t1 + tn)
2
1.
Find S500 for the AP 7, 11, 15, …
2.
Find S100 for the AP 95, 92, 89, …
3.
Find S50 for the AP -36, -31, -26, …
4.
Find S20 for the AP -18, -20, -22, …
5.
(a) Find the number of terms in this AP 5, 8, 11, …92.
(b) Find the sum of the terms of the AP in (a).
6.
Find the sum of the AP 2, 7, 12, … 87.
For the geometric series
a + ar2 + ar3 +…
the sum of n terms is given by
a(r  1)
Sn 
r 1
n
or
a(1  r n )
Sn 
1 r
Use this when
Use this when
r>1
r<1
Find S20 for the GP

3, 15, 75, 225,…
Here a = 3, r = 5 and n = 20
3(5  1)
S 20 
5 1
20
S20 = 7.15 x 1013
Find S50 for the GP: 2, 6, 18, 54,…

Here a = 2 and r = 3, n = 50
2(3  1)
S50 
3 1
50
= 350 – 1 (leave in this form)
Try these. Leave large powers in index form
1.
Find S20 for the GP: 1, 2, 4, 8, …
2.
Find S50 for the GP: 2, -6, 18, -54, …
3.
Find S12 for the GP: 1, 1/3, 1/9, 1/27, …
4.
Find S30 for the GP: 4, -2, 1, - ½ , ¼,…
5.
Find S15 for the GP: 2, 0.2, 0.02, 0.002, …
Infinite series – the limit of a sum


A series may have a limit
For some series, as more terms are added on,
the sums produced approach nearer and nearer
to a particular value. The value ℓ is called the
SUM TO INFINITY of the series and we say the
series is CONVERGENT.
lim
Sn  
n
Infinite series – the limit of a sum
If, as more terms are added Sn gets larger or
more negative without approaching a
particular value, or oscillates, then the
series does not have a limit and we say it
is DIVERGENT.
Are these series convergent or divergent?

2 + 6 + 10 + 14 + 18 + 22 + 26 + 30 + 34 +…
S1 = 2
S2 = 8
S3 = 18
S4 = 32
S5 = 50
S6 = 72
S7 = 98
S8 = 128
S9 = 162
As n increases Sn is also increasing without approaching a
particular value so the series is divergent.
Are these series convergent or divergent?

9 + 3 + 1 + 1/3 + 1/9 + 1/27 + …
S1 = 9
S2 = 12
S3 = 13
S4 = 13.3333 33
S5 = 13.444444
S6 = 13.481481
S7 = 13.493827
S8 = 13.497942
S9 = 13.499314
The sums appear to be getting closer to 13.5. So we say
that the series is convergent and the sum to infinity is
13.5.
lim
Sn =
 13.5
n
For each of the following series:
b.
Find S1 to S10 at least.
State whether the series is convergent or divergent
and a value accordingly.
1.
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + …
2.
1 + 1/3 + 1/9 + 1/27 + …
3.
2 + -1 + -4 + -7 + …
4.
¼+½+1+2+…
a.
Limit of an arithmetic series
Any arithmetic series is divergent
Limit of a geometric series

Not all geometric series have a limit

If r ≥ 1, Sn increases without end

If r ≤ -1, Sn oscillates.

If -1 < r < 1 Sn will have a limit and the series is
convergent
Limit of a geometric series

Formula for the sum to infinity of a series is:
a(1  r n )
S 
1 r
For -1 < r < 1. BUT as n takes larger and larger
values, rn gets closer and closer to zero.

Therefore the formula becomes
a
S 
1 r
Limit of a geometric series

For the series 4 + 1 + ¼ + 1/16 + …
a = 4,
r=¼
S 
4
1
1
4
4
..... 
aaaa
3
a
4
1
aaaa
.....  5.3333...(5 )
a
3
a
Sn 
1 r
Which of the following series are convergent?
For those which are, find the value of S∞.
1.
Is a geometric series
9 + 9/2 + 9/4 + 9/8 + …
With a = 9 and 2 = 1/2 . Since -1 < r < 1, the series is
convergent.
9
a
S 
Sn 
1
1 r
1
9
a..... 
1
2
a.....  18
2
Which of the following series are convergent?
For those which are, find the value of S∞.
2. -3 + -1 + 1 + 3 + …
Is an arithmetic series and is therefore divergent
3. 1/10 + 1 + 10 + 100 + …
Is a geometric series with a = 1/10 and r = 10. since
r > 1, the series is divergent