Download Cell Mechanics

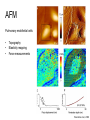
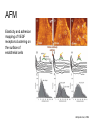
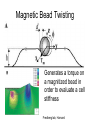
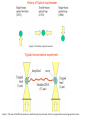
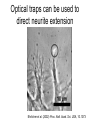
Techniques for measuring
cell mechanics
• Glass microneedle
• Atomic Force Microscopy
• Optical/Magnetic Tweezers
• Traction Force Microscopy
• Micropost Array
–
Note: all materials, if not acknowledged are modified from the notes from Dr Kas’s lab
in Liepzig or from the PhD disseration of Aruna Ranaweera or from Dr Lal’s lab work
Measurement of the mechanical
properties of actin
Glass
microneedle
measurements
The elastic
modulus of
alpha-actin fibers
is about 0.1Pa
The tensile
strength is
around 100pN
Kishino & Yanagito. Nature. 1988
Atomic Force Microscopy
Lal & Arnsdorf, 2010
Bruker Bioscope SZ
Physical Principle of AFM imaging
From Kas Lab, Germany
AFM force curve during a typical experiment
http://www.nanoscience.com/education/i/F-z_curve.gif
Trace: First the cantilever is moved down without touching the sample, i.e. no deflection but a declining distance is measured (1).
Very close to the surface the cantilever can be suddenly attracted by the sample due to adhesion forces (e.g. electrostatic
interaction), i.e. the cantilever flicks down the remaining distance and gives a small downward deflection (2). When the
cantilever is moved further down, the cantilever is bent upwards in direct proportion to the z-piezo height (3). This characteristic
linear slope can be used for calibration of the cantilever.
Retrace: As soon as a defined setpoint of deflection is reached (4), the cantilever is withdrawn. The cantilever gets more and
more unbent, while moving upwards again (5). Then, the tip usually keeps attracted to the surface by adhesion, which causes the
cantilever to bend in the opposite direction, until it suddenly loses contact and flicks up into its initial position (6). Further
retraction results no longer in a vertical deflection (7).
When the cantilever is calibrated, i.e. its sensitivity s and spring constant k are know, it is possible to calculate the applied force F
which is proportional to the vertical cantilever deflection u.
When the cantilever is calibrated, i.e. its sensitivity s and spring constant k are
know, it is possible to calculate the applied force F which is proportional to the
vertical cantilever deflection u.
Measurement of Elastic and Viscoelastic Properties
SFM may be used to measure local elastic and viscoelastic properies of soft matter samples like biological cells. The local elastic
modulus E can be determined by recording and analyzing force-distance-curves. In order to avoid damages of living cells during the
measurement and to have well-defined probe geometry for the following calculation of the moduli, we modify commercially
available cantilevers by gluing a small polysterene bead (diameter ~ 6 µm) onto the tip. The appropriate calculations are done based
on the Hertz model.
Dynamic SFM measurements with a vibrating cantilever can be performed to quantify even the viscous properties of the
sample by determining its storage and loss modulus. In this case a modified Hertz model is used for data analysis.
When thinner samples are to be probed, the influence of the underlying hard substrate on the elasticity measurement cannot be
neglected anymore and we apply Tu and Chen corrections to the Hertz mode (next page).
SFM may be used to measure local elastic and viscoelastic properies of soft matter samples like biological cells. The local
elastic modulus E can be determined by recording and analyzing force-distance-curves. In order to avoid damages of living
cells during the measurement and to have well-defined probe geometry for the following calculation of the moduli, we
modify commercially available cantilevers by gluing a small polysterene bead (diameter ~ 6 µm) onto the tip. The
appropriate calculations are done based on the Hertz model.
Dynamic SFM measurements with a vibrating cantilever can be performed to quantify even the viscous properties of
the sample by determining its storage and loss modulus. In this case a modified Hertz model is used for data
analysis.
When thinner samples are to be probed, the influence of the underlying hard substrate on the elasticity measurement cannot
be neglected anymore and we apply Tu and Chen corrections to the Hertz model.
The point of contact is determined from a curve fit of unloading data
AFM can be used to measure the
compliance of a cell or the adhesion
force of cell attachment molecules
Wojcikiewicz et al., 2004
AFM
Pulmonary endothelial cells
•
•
•
Topography
Elasticity mapping
Force measurements
Teran Arce et al., 2008
AFM
Elasticity and adhesion
mapping of VEGF
receptors clustering on
the surface of
endothelial cells
Almqvist et al., 2004
Issues with AFM
• Infinite half space assumption
• Surface tension
• Dynamics of cytoskeleton
Magnetic Bead Twisting
Generates a torque on
a magnitized bead in
order to evaluate a cell
stiffness
Fredberg lab, Harvard
Optical Tweezer
•The optical tweezer is a device that uses a focused laser beam to trap and manipulate individual dielectric particles in an aqueous medium.
•The laser beam is sent through a high numerical aperture (highly converging) microscope objective that is used for both trapping and viewing
particles of interest (Figure 1).
•Known more descriptively as “single-beam gradient force optical traps”, optical tweezers are also called “laser tweezers” and “single focused
laser beam traps”.
Figure 1: Basic optical tweezer. A single laser beam is focused to a diffraction-limited spot using a high numerical aperture
microscope objective. Dielectric particles are trapped near the laser focus.
History of Optical trap/tweezer
Figure 2: Evolution of optical tweezers
Typical biomechanics experiment
Figure 3: The ends of the DNA molecule are attached to polystyrene beads which are trapped and moved using optical tweezers.
Basic Principle
•
For a dielectric particle trapped using an optical tweezer, the main optical forces can be divided into two categories:
•
•
i. Nonconservative absorption and scattering forces and
Ii. Conservative gradient forces.
•
(Absorption forces can be minimized by choosing a trapping frequency that is off-resonance. Hence, only the
scattering force and the gradient force are considered significant for optical tweezers.)
•
The scattering force
1.
arises due to the direct scattering of photons due to incoherent interaction of light with matter.
2. acts in the same direction as incident light and is proportional to the intensity of incident light.
•
The gradient force
1. occurs whenever a transparent material with a refractive index greater than its surrounding medium is placed
within a light gradient.
2. acts in the direction of increasing light intensity and is proportional to the gradient of light intensity.
•
If a dielectric particle is placed within the narrow waist of a sharply focused beam of
light, the scattering force will have a tendency to push the particle away, while the
gradient force will have a tendency to hold the particle within the waist (Figure 4).
Gradient force
scattering force
Figure 4: Optical forces.
Stable trapping occurs when the gradient force is strong enough to overcome the
scattering force.
(A strong gradient force can be achieved by using a high numerical aperture2 (NA) lens to
focus a laser beam to a diffraction-limited spot).
Physical explanation
Interaction of photons and matters can occur in two boundary conditions
A. Rayleigh Regime (D << λ)
In the Rayleigh regime, the particle is very small compared to the wavelength (D << λ). The distinction between the
components of reflection, refraction and diffraction can be ignored. Since the perturbation of the incident wave front is minimal, the
particle can be viewed as an induced dipole behaving according to simple electromagnetic laws.
NOT COMMONLY USED FOR BIOLOGICAL SYSTEMS and hence ignored
B. Ray Optics Regime (D >> λ)
In the ray optics regime, the size of the object is much larger than the wave lenght of the light, and a single beam can
be tracked throughout the particle. (This situation is for example when whole cells are trapped using infrared light while suspended in
solution. The incident laser beam can be decomposed into individual rays with appropriate intensity, momentum, and direction. These rays
propagate in a straight line in uniform, nondispersive media and can be described by geometrical optics)
According to this model, “the basic operation of optical tweezers can be explained by the momentum transfer
associated with the redirection of light at a dielectric interface”.
When light hits a dielectric interface, part of the light is refracted and part of it is reflected. Figure 5 shows a light ray
with momentum ~pi being incident upon a dielectric sphere with an index of refraction higher than the medium surrounding it.
•The light momentum reflected at the first interface is pi1,
•the light momentum that exits from the sphere after refraction at the second interface is pi2.
(In reality, a small fraction of the light ray will be reflected back into the sphere, causing an
infinite number of internal reflections, but this can be ignored during a first approximation)
The net change of momentum of the single ray of light, Dpi = pi1+ pi2 - pi
By representing the light beam as a collection of light rays, the total change of light momentum is
From Newton’s Second Law, the resulting force acting on the light is given by the rate of change of light momentum
According to Newton’s Third Law, the dielectric sphere will experience an equal and opposite trapping force
Figure 5: Qualitative ray optics model
•The above equations ignore internal reflections and polarization effects.
•The net effect of internal reflections is to add to the scattering force, making the trap weaker.
•In practice, the equilibrium position of the sphere lies slightly beyond the focal point of the beam.
•In fact, ray optics theory predicts that the exact equilibrium location of the trap should be approximately 3•5% of the sphere diameter beyond the laser focus.
•Polystyrene (C8H8) beads are commonly used for trapping.
•Polystyrene has a density of 1040-1070 kg/m3,
•dielectric constant of 2-2.8,
•electric resistivity of 1013-1015 Ώm,
•heat capacity of 1200-2100 J/kg.K,
•thermal conductivity of 0.12-0.193 W/m.K,
•and visible transmission of 80-90%.
•Since water and polystyrene have almost identical densities, the net force due to gravity can be neglected.
Optical traps can be used to
direct neurite extension
Ehrlicher et al. (2002) Proc. Natl. Acad. Sci. USA, 10.1073
Summary
• Cell cytoskeleton composed of actin filaments,
microtubules and intermediate filaments
• Actin filaments resist tension, are polarized and can
catastrophically extend and collapse
• Microtubules resist compression, are polarized and show
treadmilling behavior
• Atomic force microscopy uses low-force indentation of
the cell membrane to study cell mechanics.
• Traction force microscopy observes a cell’s ability to
deform its surroundings to compute shear stress and,
indirectly, cell force.
Summary
• Traction force microscopy observes a
cell’s ability to deform its surroundings to
compute shear stress and, indirectly, cell
force.
• Micropost array deflection can also be
used to observe a cell’s traction force.
• Optical traps can produce very small
forces that can be used to direct neurite
extension.