* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Cell Mechanics
Ray tracing (graphics) wikipedia , lookup
Silicon photonics wikipedia , lookup
Cross section (physics) wikipedia , lookup
Surface plasmon resonance microscopy wikipedia , lookup
3D optical data storage wikipedia , lookup
Confocal microscopy wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Ellipsometry wikipedia , lookup
Optical coherence tomography wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Super-resolution microscopy wikipedia , lookup
Interferometry wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Nonimaging optics wikipedia , lookup
Atmospheric optics wikipedia , lookup
Nonlinear optics wikipedia , lookup
Vibrational analysis with scanning probe microscopy wikipedia , lookup
Photon scanning microscopy wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Retroreflector wikipedia , lookup
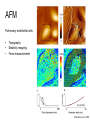
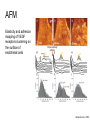
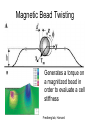
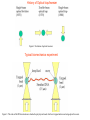
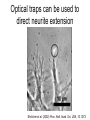
Techniques for measuring cell mechanics • Glass microneedle • Atomic Force Microscopy • Optical/Magnetic Tweezers • Traction Force Microscopy • Micropost Array – Note: all materials, if not acknowledged are modified from the notes from Dr Kas’s lab in Liepzig or from the PhD disseration of Aruna Ranaweera or from Dr Lal’s lab work Measurement of the mechanical properties of actin Glass microneedle measurements The elastic modulus of alpha-actin fibers is about 0.1Pa The tensile strength is around 100pN Kishino & Yanagito. Nature. 1988 Atomic Force Microscopy Lal & Arnsdorf, 2010 Bruker Bioscope SZ Physical Principle of AFM imaging From Kas Lab, Germany AFM force curve during a typical experiment http://www.nanoscience.com/education/i/F-z_curve.gif Trace: First the cantilever is moved down without touching the sample, i.e. no deflection but a declining distance is measured (1). Very close to the surface the cantilever can be suddenly attracted by the sample due to adhesion forces (e.g. electrostatic interaction), i.e. the cantilever flicks down the remaining distance and gives a small downward deflection (2). When the cantilever is moved further down, the cantilever is bent upwards in direct proportion to the z-piezo height (3). This characteristic linear slope can be used for calibration of the cantilever. Retrace: As soon as a defined setpoint of deflection is reached (4), the cantilever is withdrawn. The cantilever gets more and more unbent, while moving upwards again (5). Then, the tip usually keeps attracted to the surface by adhesion, which causes the cantilever to bend in the opposite direction, until it suddenly loses contact and flicks up into its initial position (6). Further retraction results no longer in a vertical deflection (7). When the cantilever is calibrated, i.e. its sensitivity s and spring constant k are know, it is possible to calculate the applied force F which is proportional to the vertical cantilever deflection u. When the cantilever is calibrated, i.e. its sensitivity s and spring constant k are know, it is possible to calculate the applied force F which is proportional to the vertical cantilever deflection u. Measurement of Elastic and Viscoelastic Properties SFM may be used to measure local elastic and viscoelastic properies of soft matter samples like biological cells. The local elastic modulus E can be determined by recording and analyzing force-distance-curves. In order to avoid damages of living cells during the measurement and to have well-defined probe geometry for the following calculation of the moduli, we modify commercially available cantilevers by gluing a small polysterene bead (diameter ~ 6 µm) onto the tip. The appropriate calculations are done based on the Hertz model. Dynamic SFM measurements with a vibrating cantilever can be performed to quantify even the viscous properties of the sample by determining its storage and loss modulus. In this case a modified Hertz model is used for data analysis. When thinner samples are to be probed, the influence of the underlying hard substrate on the elasticity measurement cannot be neglected anymore and we apply Tu and Chen corrections to the Hertz mode (next page). SFM may be used to measure local elastic and viscoelastic properies of soft matter samples like biological cells. The local elastic modulus E can be determined by recording and analyzing force-distance-curves. In order to avoid damages of living cells during the measurement and to have well-defined probe geometry for the following calculation of the moduli, we modify commercially available cantilevers by gluing a small polysterene bead (diameter ~ 6 µm) onto the tip. The appropriate calculations are done based on the Hertz model. Dynamic SFM measurements with a vibrating cantilever can be performed to quantify even the viscous properties of the sample by determining its storage and loss modulus. In this case a modified Hertz model is used for data analysis. When thinner samples are to be probed, the influence of the underlying hard substrate on the elasticity measurement cannot be neglected anymore and we apply Tu and Chen corrections to the Hertz model. The point of contact is determined from a curve fit of unloading data AFM can be used to measure the compliance of a cell or the adhesion force of cell attachment molecules Wojcikiewicz et al., 2004 AFM Pulmonary endothelial cells • • • Topography Elasticity mapping Force measurements Teran Arce et al., 2008 AFM Elasticity and adhesion mapping of VEGF receptors clustering on the surface of endothelial cells Almqvist et al., 2004 Issues with AFM • Infinite half space assumption • Surface tension • Dynamics of cytoskeleton Magnetic Bead Twisting Generates a torque on a magnitized bead in order to evaluate a cell stiffness Fredberg lab, Harvard Optical Tweezer •The optical tweezer is a device that uses a focused laser beam to trap and manipulate individual dielectric particles in an aqueous medium. •The laser beam is sent through a high numerical aperture (highly converging) microscope objective that is used for both trapping and viewing particles of interest (Figure 1). •Known more descriptively as “single-beam gradient force optical traps”, optical tweezers are also called “laser tweezers” and “single focused laser beam traps”. Figure 1: Basic optical tweezer. A single laser beam is focused to a diffraction-limited spot using a high numerical aperture microscope objective. Dielectric particles are trapped near the laser focus. History of Optical trap/tweezer Figure 2: Evolution of optical tweezers Typical biomechanics experiment Figure 3: The ends of the DNA molecule are attached to polystyrene beads which are trapped and moved using optical tweezers. Basic Principle • For a dielectric particle trapped using an optical tweezer, the main optical forces can be divided into two categories: • • i. Nonconservative absorption and scattering forces and Ii. Conservative gradient forces. • (Absorption forces can be minimized by choosing a trapping frequency that is off-resonance. Hence, only the scattering force and the gradient force are considered significant for optical tweezers.) • The scattering force 1. arises due to the direct scattering of photons due to incoherent interaction of light with matter. 2. acts in the same direction as incident light and is proportional to the intensity of incident light. • The gradient force 1. occurs whenever a transparent material with a refractive index greater than its surrounding medium is placed within a light gradient. 2. acts in the direction of increasing light intensity and is proportional to the gradient of light intensity. • If a dielectric particle is placed within the narrow waist of a sharply focused beam of light, the scattering force will have a tendency to push the particle away, while the gradient force will have a tendency to hold the particle within the waist (Figure 4). Gradient force scattering force Figure 4: Optical forces. Stable trapping occurs when the gradient force is strong enough to overcome the scattering force. (A strong gradient force can be achieved by using a high numerical aperture2 (NA) lens to focus a laser beam to a diffraction-limited spot). Physical explanation Interaction of photons and matters can occur in two boundary conditions A. Rayleigh Regime (D << λ) In the Rayleigh regime, the particle is very small compared to the wavelength (D << λ). The distinction between the components of reflection, refraction and diffraction can be ignored. Since the perturbation of the incident wave front is minimal, the particle can be viewed as an induced dipole behaving according to simple electromagnetic laws. NOT COMMONLY USED FOR BIOLOGICAL SYSTEMS and hence ignored B. Ray Optics Regime (D >> λ) In the ray optics regime, the size of the object is much larger than the wave lenght of the light, and a single beam can be tracked throughout the particle. (This situation is for example when whole cells are trapped using infrared light while suspended in solution. The incident laser beam can be decomposed into individual rays with appropriate intensity, momentum, and direction. These rays propagate in a straight line in uniform, nondispersive media and can be described by geometrical optics) According to this model, “the basic operation of optical tweezers can be explained by the momentum transfer associated with the redirection of light at a dielectric interface”. When light hits a dielectric interface, part of the light is refracted and part of it is reflected. Figure 5 shows a light ray with momentum ~pi being incident upon a dielectric sphere with an index of refraction higher than the medium surrounding it. •The light momentum reflected at the first interface is pi1, •the light momentum that exits from the sphere after refraction at the second interface is pi2. (In reality, a small fraction of the light ray will be reflected back into the sphere, causing an infinite number of internal reflections, but this can be ignored during a first approximation) The net change of momentum of the single ray of light, Dpi = pi1+ pi2 - pi By representing the light beam as a collection of light rays, the total change of light momentum is From Newton’s Second Law, the resulting force acting on the light is given by the rate of change of light momentum According to Newton’s Third Law, the dielectric sphere will experience an equal and opposite trapping force Figure 5: Qualitative ray optics model •The above equations ignore internal reflections and polarization effects. •The net effect of internal reflections is to add to the scattering force, making the trap weaker. •In practice, the equilibrium position of the sphere lies slightly beyond the focal point of the beam. •In fact, ray optics theory predicts that the exact equilibrium location of the trap should be approximately 3•5% of the sphere diameter beyond the laser focus. •Polystyrene (C8H8) beads are commonly used for trapping. •Polystyrene has a density of 1040-1070 kg/m3, •dielectric constant of 2-2.8, •electric resistivity of 1013-1015 Ώm, •heat capacity of 1200-2100 J/kg.K, •thermal conductivity of 0.12-0.193 W/m.K, •and visible transmission of 80-90%. •Since water and polystyrene have almost identical densities, the net force due to gravity can be neglected. Optical traps can be used to direct neurite extension Ehrlicher et al. (2002) Proc. Natl. Acad. Sci. USA, 10.1073 Summary • Cell cytoskeleton composed of actin filaments, microtubules and intermediate filaments • Actin filaments resist tension, are polarized and can catastrophically extend and collapse • Microtubules resist compression, are polarized and show treadmilling behavior • Atomic force microscopy uses low-force indentation of the cell membrane to study cell mechanics. • Traction force microscopy observes a cell’s ability to deform its surroundings to compute shear stress and, indirectly, cell force. Summary • Traction force microscopy observes a cell’s ability to deform its surroundings to compute shear stress and, indirectly, cell force. • Micropost array deflection can also be used to observe a cell’s traction force. • Optical traps can produce very small forces that can be used to direct neurite extension.