* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 1 ELEC 3105 OLD slides
Fundamental interaction wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Circular dichroism wikipedia , lookup
History of quantum field theory wikipedia , lookup
Magnetic monopole wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Speed of gravity wikipedia , lookup
Electromagnetism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Maxwell's equations wikipedia , lookup
Lorentz force wikipedia , lookup
Field (physics) wikipedia , lookup
Lecture 1 ELEC 3105
Basic E&M and Power
Engineering
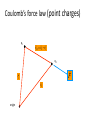
Coulomb’s Force
law
Coulomb’s force law (point charges)
q1
r12 r2 r1
q2
r1
origin
r2
F
Coulomb’s force law (point charges)
q1
r12 r2 r1
q2
r1
origin
r2
F
kq1q2
F12 2 r12
r12
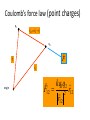
Coulomb’s force law (point charges)
q1
r12 r2 r1
q2
r1
r2
F
origin
[F]-force; Newtons {N}
[q]-charge; Coulomb {C}
[r]-distance; meters {m}
[]-permittivity; Farad/meter {F/m}
kq1q2
F12 2 r12
r12
Property of the medium
Coulomb’s force law (point charges)
q1
r12 r2 r1
q2
r1
r2
F
Point charges of the same sign
origin
kq1q2
F12 2 r12
r12
q1, q2 0,0
q1, q2 0,0
Repulsive force
F12 0
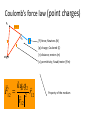
Coulomb’s force law (point charges)
q1
r12 r2 r1
q2
r1
r2
F
Point charges of the opposite sign
origin
kq1q2
F12 2 r12
r12
q1 0, q2 0 ,
q1 0, q2 0 ,
Attractive force
F12 0
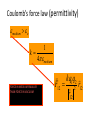
Coulomb’s force law (permittivity)
For a medium like air
medium 1.0006 o
Relative permittivity
medium
r
o
Coulomb’s force law (permittivity)
medium o
k
FORCE IN MEDIUM SMALLER
THAN FORCE IN VACUUM
1
4medium
kq1q2
F12 2 r12
r12
Lecture 1 (97.315)
Basic E&M and Power
Engineering
Coulomb's Law
The force exerted by one point charge on another acts along the line joining the
charges. It varies inversely as the square of the distance separating the charges
and is proportional to the product of the charges. The force is repulsive if the
charges have the same sign and attractive if the charges have opposite signs.
Action at a distance
Lecture 1 (97.315)
Basic E&M and Power
Engineering
Electric field
intensity
Electric field intensity (point charges)
Consider the region around a single point charge
q2
Electric field intensity (point charges)
F
Other charges brought near this
charge would experience a force
whose magnitude depends on the
distance between q1 and q2.
q1
r21
q2
kq1q2
F21 2 r21
r21
Electric field intensity (point charges)
The existence of this force can be
described by saying that the charge q2
produces an electric field in the
surrounding region.
q2
Electric field intensity (point charges)
Since Force is proportional to q2 it
makes sense to define the electric field
as:
q2
F
E
q1
Electric field intensity (point charges)
P
r
q2
Observation point
Electric field is defined at any point
in space. Electric field is a vector
quantity.
kq2 r
E 2
r
Valid for a point charge
Electric field intensity (point charges)
[k]-Coulomb constant; meter/Farad {m/F}
kq2 r
E 2
r
[q]-charge; Coulomb {C}
[r]-distance; meters {m}
[E]-Electric field; Newton/Coulomb {N/C}
[E]-Electric field; Volt/meter {V/m}
P
r
q2
Observation point
Electric field intensity (point charges)
F
E
q1
P
r
q2
Observation point
Comments:
(1) Electric field is a vector quantity. Thus
at all points where the electric field exists it
has magnitude and direction.
Electric field intensity (point charges)
F
E
q
P
r
Q
Observation point
Comments:
(2) The charge q1, test charge, is usually
written as q and must be small and positive
such that it does not disturb the source
charge q2 = Q.
Electric field intensity (point charges)
F
E
q
P
r
Q
Observation point
Comments:
(3) For a positive source charge Q the
electric field vector and the electric force on
the test charge q are in the same direction.a
Electric field intensity (point charges)
F
E
q
P
r
Q
Observation point
Comments:
(4) For a positive source charge Q, the
electric field lines are directed away from
the charge.
Electric field intensity (point charges)
F
E
q
P
r
Q
Observation point
Comments:
(5) For a point charge Q located at the
origin the electric field vector is:
kQ
E 2 r
r
Electric field (charge distribution)
Electric field (charge distribution)
q1
z
r1
P
r2
q2
r
Two point charges
y
x
General expression for
electric field produced by a
single point charge Q a
distance r from the
observation point P:
kQ
E 2 r
r
Electric field (charge distribution)
E1
q1
z
P
q2
E2
Two point charges
y
x
The electric field obeys the
law of linear superposition
EP E1 E2
Electric field (charge distribution)
r r1
q1
z
r1
P
q2
r
Two point charges
y
x
Electric field produced by
charge q1 at P
kq1
r r1
E1 2
r r1
r r1
Electric field (charge distribution)
q1
z
r2
q2
r r2
r
P
Two point charges
y
x
Electric field produced by
charge q2 at P
kq2
E2 2
r r2
r r2
r r2
Electric field (charge distribution)
q1
z
r1
r2
q2
r r1
r r2
r
P
Two point charges
y
x
kq1
E2 2
r r1
kq2
r r1
2
r r1
r r2
r r2
r r2
Electric field (charge distribution)
qi
z
r ri
ri
q3
q1
P
q2
r
qN
q4
y
Large number N
of point charges
x
q5
r ri
E k qi 3
r ri
i 1
N
PRINCIPLE OF SUPERPOSITION
Given a group of charges we find the net electric field at any point in space by using
the principle of superposition. This is a general principle that says a net effect is the
sum of the individual effects. Here, the principle means that we first compute the
electric field at the point in space due to each of the charges, in turn. We then find the
net electric field by adding these electric fields vectorially, as usual.
Electric field (charge distribution)
q
Charged volume
Charge always occurs in
integer multiples of the
electric charge e = 1.6X1019C.
Charged surface
In is often useful to imagine that there is a
continuous distribution of charge
Charged line
Electric field (charge distribution)
P
Charge volume element dV
q
Charged volume
The electric field at the point P is obtained by
summing the electric field contribution from
from each volume element dV.
V
Volume charge density
V
V dV
Units; {C/m3}
Charge in dV
When the volume element
dV--> 0
Sum --> Integral
Electric field (charge distribution)
P
V
dV
dE
r
Field for one element
V
rkdq
dE 2
r
Charged volume
With
rkV dV
dE
2
r
dq V dV
Integration over
volume V
r kV dV
E dE 2
r
V
V
Electric field (charge distribution)
V may be a function of the coordinates
usually a constant
dV dxdydz,.....
unit vector
function of (x,y,z),….
r kV dV
E dE 2
r
V
V
2
2
2
r x y z ,....
k
1
4
usually a constant when medium is uniform
Electric field (charge distribution)
P
dS
q
Charged surface
The electric field produced at the
point P is:
Charge surface element dS
s
Surface charge density
s
s dS
Units; {C/m2}
Charge on dS
r k s dS
E dE 2
r
S
S
Electric field (charge distribution)
s may be a function of the coordinates
usually a constant
dS dxdy,.....
unit vector
function of (x,y,z),….
r k s dS
E dE 2
r
S
S
2
2
2
r x y z ,....
k
1
4
usually a constant when medium is uniform
Electric field (charge distribution)
P
d
q
Charged line
Charged line element d
Linear charge density
d
The electric field produced at the
point P is:
Units; {C/m}
Charge on
r k d
E dE 2
r
L
L
d
Electric field (charge distribution)
may be a function of the coordinates
usually a constant
d dx,.....
unit vector
function of (x,y,z),….
r k d
E dE 2
r
L
L
2
2
2
r x y z ,....
k
1
4
usually a constant when medium is uniform
Electric field (charge distribution)
z
P (0,0,h)
Example: Ring charged line
b
x
y
A ring of charge of radius b is characterized by a uniform line charge
density of positive polarity, With the ring in free space and
positioned in the x-y plane, determine the electric field intensity
at the point P(0,0,h) along the axis of the ring a distance h from its
center.
E
Electric field (charge distribution)
z
P (0,0,h)
Solution: Ring charged line
b
x
y
Start by considering the electric field produced by a small segment
of the ring. Then we san sum “integrate” over the entire ring to get
the net electric field
E
Electric Field on the Axis of a Ring of Charge
We determine the field at point P on the axis of the ring. It should be apparent from
symmetry that the field is along the axis. The field dE due to a charge element dq is
shown, and the total field is just the superposition of all such fields due to all charge
elements around the ring. The perpendicular fields sum to zero, while the differential xcomponent of the field is
We now integrate, noting that r and x are constant for all points on the ring:
This gives the predicted result. Note that for x much larger than a (the radius of the ring),
this reduces to a simple Coulomb field. This must happen since the ring looks like a point
as we go far away from it. Also, as was the case for the gravitational field, this field has
extrema at x = +/-a.