Introduction to Hyperbolic Geometry - Conference
... Although fifth postulate has since been stated in simpler forms ( Through a point not on a given straight line, one and only one line can be drawn that never meets the given line[Hilbert‟s parallel postulate] ). Mathematicians were still troubled by its complexity, and were convinced that it could b ...
... Although fifth postulate has since been stated in simpler forms ( Through a point not on a given straight line, one and only one line can be drawn that never meets the given line[Hilbert‟s parallel postulate] ). Mathematicians were still troubled by its complexity, and were convinced that it could b ...
Inscribed Angles, Secant Angles, and Tangent Segments
... March 23, 2016 Def: A chord of a circle is a line segment that connects two points of the circle. Def: A diameter of a circle is a chord that contains the center. The diameter of a circle is the length of one of these chords. Theorem 56: If a line through the center of a circle is perpendicular t ...
... March 23, 2016 Def: A chord of a circle is a line segment that connects two points of the circle. Def: A diameter of a circle is a chord that contains the center. The diameter of a circle is the length of one of these chords. Theorem 56: If a line through the center of a circle is perpendicular t ...
Acute Angle - An angle that measures less than 90
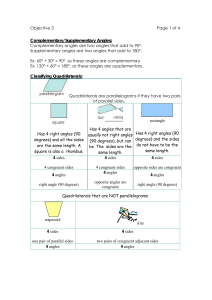
... Parallelograms – a quadrilateral with two pairs of parallel sides; opposite sides have the same length, and opposite angles have the same measure ...
... Parallelograms – a quadrilateral with two pairs of parallel sides; opposite sides have the same length, and opposite angles have the same measure ...
Dividing a decimal by a whole number
... Topic VII Properties of Circles Vocabulary Circle - Is the set of all points in a plane equidistant from a given point called the center of the circle. Radius: Any segment with endpoints that are the center of the circle and a point on the circle. Chord: Segments with endpoints that are on the circ ...
... Topic VII Properties of Circles Vocabulary Circle - Is the set of all points in a plane equidistant from a given point called the center of the circle. Radius: Any segment with endpoints that are the center of the circle and a point on the circle. Chord: Segments with endpoints that are on the circ ...
Spherical Geometry Activities - Notes
... on the sphere. How would you describe it? Why does the great circle correspond to a line on the plane?] The extensions will meet up with each other; put another way, if you go along a great circle then you will eventually return to your starting point. [The great circle is the largest circle that is ...
... on the sphere. How would you describe it? Why does the great circle correspond to a line on the plane?] The extensions will meet up with each other; put another way, if you go along a great circle then you will eventually return to your starting point. [The great circle is the largest circle that is ...
Spherical Triangles and Girard`s Theorem
... Great circles play the role of straight lines in spherical geometry. Given two distinct points on S 2 , there is a great circle passing through them obtained by the intersection of S 2 with the plane passing through the origin and the two given points. ...
... Great circles play the role of straight lines in spherical geometry. Given two distinct points on S 2 , there is a great circle passing through them obtained by the intersection of S 2 with the plane passing through the origin and the two given points. ...
Geometry Curriculum 2011-12
... Critical Area 1: In previous grades, students were asked to draw triangles based on given measurements. They also have prior experience with rigid motions: translations, reflections, and rotations and have used these to develop notions about what it means for two objects to be congruent. In this uni ...
... Critical Area 1: In previous grades, students were asked to draw triangles based on given measurements. They also have prior experience with rigid motions: translations, reflections, and rotations and have used these to develop notions about what it means for two objects to be congruent. In this uni ...
Inverses Contrapositive Indirect Reasoning - If-you-give
... at the same time. Examine each pair of statements to see whether they contradict each other. II and III I and II I and III P, Q, and R are P, Q, and R are P, Q, and R are collinear, and coplanar and coplanar, and m PQR = 60. collinear. m PQR PQR==60. ...
... at the same time. Examine each pair of statements to see whether they contradict each other. II and III I and II I and III P, Q, and R are P, Q, and R are P, Q, and R are collinear, and coplanar and coplanar, and m PQR = 60. collinear. m PQR PQR==60. ...
Document
... Theorem 1: Suppose a line is parallel to one side of a triangle and intersects the other two sides in different points. Then, this line divides the intersected sides into ...
... Theorem 1: Suppose a line is parallel to one side of a triangle and intersects the other two sides in different points. Then, this line divides the intersected sides into ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.