File
... 1. Undefined Terms in Geometry > have no exact definition, just a description Point * exact location/position on a plane surface * represented by a dot & named with a capital letter A Line * straight, no thickness & extends in both directions w/o end * set of infinite points ...
... 1. Undefined Terms in Geometry > have no exact definition, just a description Point * exact location/position on a plane surface * represented by a dot & named with a capital letter A Line * straight, no thickness & extends in both directions w/o end * set of infinite points ...
Problem Task - CMS Secondary Math Wiki
... definitions and diagrams of each type of segment. Students sometimes get confused identifying central and inscribed angles and, therefore, use the wrong formula to compute angle measures. Perhaps making a connection that a central angle has its vertex in the center of the circle will help students d ...
... definitions and diagrams of each type of segment. Students sometimes get confused identifying central and inscribed angles and, therefore, use the wrong formula to compute angle measures. Perhaps making a connection that a central angle has its vertex in the center of the circle will help students d ...
SYNTHETIC PROJECTIVE GEOMETRY
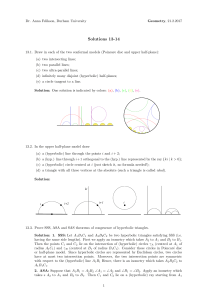
... 4. Let (P, L) be an incidence plane, let L be a line in P , let X be a point in P which does not lie on L, and assume that M1 , · · · Mk are lines which pass through X and meet L in points Y1 , · · · Yk respectively. Prove that the points Y 1 , · · · Yk are distinct if and only if the lines M1 , · · ...
... 4. Let (P, L) be an incidence plane, let L be a line in P , let X be a point in P which does not lie on L, and assume that M1 , · · · Mk are lines which pass through X and meet L in points Y1 , · · · Yk respectively. Prove that the points Y 1 , · · · Yk are distinct if and only if the lines M1 , · · ...
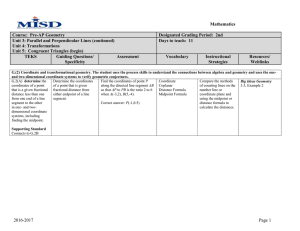
TEKS Snapshot – Geometry
... distinguish between undefined terms, definitions, postulates, conjectures, and theorems identify and determine the validity of the converse, inverse, and contrapositive of a conditional statement and recognize the connection between a biconditional statement and a true conditional statement with a t ...
... distinguish between undefined terms, definitions, postulates, conjectures, and theorems identify and determine the validity of the converse, inverse, and contrapositive of a conditional statement and recognize the connection between a biconditional statement and a true conditional statement with a t ...
Unit 4 Circles Geometry ACC - Long Beach Unified School District
... • Students will identify and explain why inscribed angles on a diameter are right angles. • Students will identify and explain why the radius of a circle is perpendicular to the tangent where the radius intersects the circle. • Students will prove properties of angles for a quadrilateral inscribed i ...
... • Students will identify and explain why inscribed angles on a diameter are right angles. • Students will identify and explain why the radius of a circle is perpendicular to the tangent where the radius intersects the circle. • Students will prove properties of angles for a quadrilateral inscribed i ...
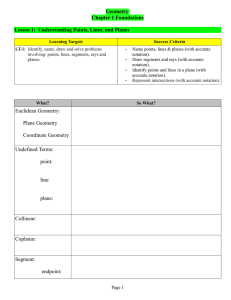
Geometry Chapter 1 Foundations Lesson 1
... a and b are called ________ c is called _______________ 1.6 Ex: Find the coordinates of a midpoint. 1.6 Ex: Find the coordinates of an endpoint. #1 Find the coordinates of the midpoint of AB with #2. M is the midpoint of XY . X has coordinates endpoints A(-8, 3) and B(-2, 7). (2, 7), and M has coord ...
... a and b are called ________ c is called _______________ 1.6 Ex: Find the coordinates of a midpoint. 1.6 Ex: Find the coordinates of an endpoint. #1 Find the coordinates of the midpoint of AB with #2. M is the midpoint of XY . X has coordinates endpoints A(-8, 3) and B(-2, 7). (2, 7), and M has coord ...
8th Math Unit 1 - Fairfield Township School
... c. Parallel lines are taken to parallel 8.G.2: Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence betwee ...
... c. Parallel lines are taken to parallel 8.G.2: Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence betwee ...
Triangle congruence and the Moulton plane
... geometry. So Pasch’s axiom holds in the Moulton plane. The standard axioms that define incidence geometry are also true in the Moulton plane. In particular, there exists a unique line through any two distinct points. Hilbert’s axioms on betweenness hold in the Moulton plane. For example, for any thr ...
... geometry. So Pasch’s axiom holds in the Moulton plane. The standard axioms that define incidence geometry are also true in the Moulton plane. In particular, there exists a unique line through any two distinct points. Hilbert’s axioms on betweenness hold in the Moulton plane. For example, for any thr ...
High School Geometry
... Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. (MA10‐GR.HS‐S.4‐GLE.3‐EO.a.i.1, 2) (CCSS: G‐GPE.1) PARCC Calculator neutral Complete the square to find the center and r ...
... Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. (MA10‐GR.HS‐S.4‐GLE.3‐EO.a.i.1, 2) (CCSS: G‐GPE.1) PARCC Calculator neutral Complete the square to find the center and r ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.