Lesson 12-4 Notes: Inscribed Angles
... 12-4 Inscribed Angles Highlight this theorem on pg514 in your workbook & do example 2. An intercepted arc consists of endpoints that lie on the sides of an inscribed angle and all the points of the circle between them. ...
... 12-4 Inscribed Angles Highlight this theorem on pg514 in your workbook & do example 2. An intercepted arc consists of endpoints that lie on the sides of an inscribed angle and all the points of the circle between them. ...
6-12 Comp 3 trainer notes - Math6-12TestPrep
... 14. Apply the theorems pertaining to the measures of inscribed angles and angles formed by chords, secants, and tangents. 15. Identify basic geometric constructions (e.g., bisecting angles or line segments, constructing parallels or perpendiculars). 16. Identify the converse, inverse, and contraposi ...
... 14. Apply the theorems pertaining to the measures of inscribed angles and angles formed by chords, secants, and tangents. 15. Identify basic geometric constructions (e.g., bisecting angles or line segments, constructing parallels or perpendiculars). 16. Identify the converse, inverse, and contraposi ...
Properties of Circles
... Because the radii OA and OC are equal, !OAC is an isosceles triangle with ! OCA = ! A. Thus ! A + ! A + ! AOC = π and ! BOC + ! AOC = π also. Subtracting, we find that 2! A = ! BOC and so the inscribed angle ! A is one-half the central angle ! BOC. Now consider the case where O does not lie on AB. L ...
... Because the radii OA and OC are equal, !OAC is an isosceles triangle with ! OCA = ! A. Thus ! A + ! A + ! AOC = π and ! BOC + ! AOC = π also. Subtracting, we find that 2! A = ! BOC and so the inscribed angle ! A is one-half the central angle ! BOC. Now consider the case where O does not lie on AB. L ...
March 8th- 9th Circles Review 2 File
... If 2 secants, a secant and a tangent, or 2 tangents intersect in the exterior of a circle, then the measure of the angle formed is 1/2 the positive differences of the measures of the intercepted arcs. ...
... If 2 secants, a secant and a tangent, or 2 tangents intersect in the exterior of a circle, then the measure of the angle formed is 1/2 the positive differences of the measures of the intercepted arcs. ...
U9 Review
... I can solve problems involving intersecting chords and the arcs, angles and segments created Chords o cut each other into 2 pieces each product of the pieces is equal o Create a pair of interior vertical angles, which create 2 unequal intercepted arcs The angle is half the sum of the arcs ...
... I can solve problems involving intersecting chords and the arcs, angles and segments created Chords o cut each other into 2 pieces each product of the pieces is equal o Create a pair of interior vertical angles, which create 2 unequal intercepted arcs The angle is half the sum of the arcs ...
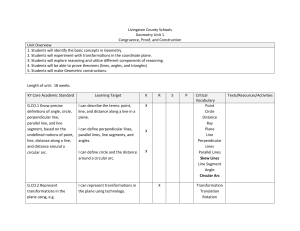
Livingston County Schools Geometry Unit 1 Congruence, Proof, and
... I can use the definition of congruence in terms of rigid motions to show that if the corresponding pairs of sides and corresponding pairs of angles of two triangles are congruent then the two triangles are congruent. ...
... I can use the definition of congruence in terms of rigid motions to show that if the corresponding pairs of sides and corresponding pairs of angles of two triangles are congruent then the two triangles are congruent. ...
Benchmark 1 - Waukee Community Schools
... Draw, construct, and describe geometrical figures and describe the relationships between them.(Slicing 3-D figures) Describe the two-dimensional figures that result from slicing three- dimensional figures, as in plane sections of right rectangular prisms and right rectangular pyramids. ...
... Draw, construct, and describe geometrical figures and describe the relationships between them.(Slicing 3-D figures) Describe the two-dimensional figures that result from slicing three- dimensional figures, as in plane sections of right rectangular prisms and right rectangular pyramids. ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.