Download Geometric Construction

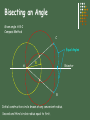
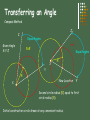
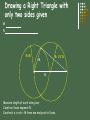
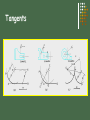
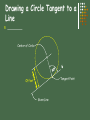
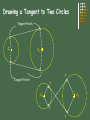
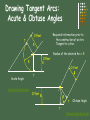
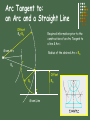
Geometric
Construction
Stephen A. Jung
Sierra College
Points and Lines


Point – represents a location in space or on a drawing
 No height, width, or depth
 Represented by the intersection of two lines
 Short cross bar on a line, or
 A small point element e.g. ( + x l )
Line – is defines as “that which has length without width”1
 Straight Line is the shortest distance between two points
 Lines can be:



Parallel – symbol = ll
Perpendicular – symbol =
Plane – is defined as:


3 points in a space
1 point and an entity with end points e.g. line or arc
1 Defined by Euclid
Angles

Angles are formed by two intersecting
lines

Common symbol = a

360 Degrees in a full circle (360o)




A degree is divided into 60 minutes (60’)
A minute is divided into 60 seconds (60”)
Example: 54o 43’ 28” is read 54 degrees, 43
minutes, and 28 seconds.
Different kinds of angles are:
Triangles

A triangle is a plane figure bounded by
three straight lines and the sum of the
interior angles is always 180o.

Types of triangles:
Quadrilaterals

A quadrilateral is a plane figure bounded
by four straight sides.

If the opposite sides are parallel, the
quadrilateral is also a parallelogram.
Polygons

A polygon is any plane figure bounded by
straight lines.

If the polygon has equal angles and equal sides,
it can be inscribed or circumscribed around a
circle, an is called a regular polygon.
Circles and Arcs


A circle is a closed curve with all points
the same distance from a point called the
center.
Attributes of a circle:
Bisecting a Line or Arc
Given line A-B or Arc A-B
Compass Method
B
A
Midpoint of line
Construction circles have the same
diameter and the radius is equal to
more than ½ the length of the line.
Bisecting an Angle
Given angle A-B-C
Compass Method
C
Equal Angles
A
R
Bisector
B
Initial construction circle drawn at any convenient radius.
Second and third circles radius equal to first.
Transferring an Angle
Compass Method
Z’
Z
Equal Angles
Given Angle
X-Y-Z
r’
R=R’
r=r’
Equal Angles
X’
r
R’
Y
R
X
New Location
Y’
Second circle radius (R’) equal to first
circle radius (R).
Initial construction circle drawn at any convenient radius.
Drawing a Triangle with sides given.
D
E
F
E
D
E
D
F
Measure length of each side given.
Construct circles from end points of base.
Drawing a Right Triangle with
only two sides given
M
N
R=M
R= 1/2 N
M
N
Measure length of each side given.
Construct base segment N.
Construct a circle = M from one end point of base.
Drawing an Equilateral Triangle
R
R
R
S
Given Side
Measure length of side given.
Draw construction circles from the end points of
the given side with the radius equal to that length.
All angles are equal to:? 60o
Drawing Regular Polygons
using CAD
Required information prior to the construction of a polygon:
1.
2.
3.
4.
Number of sides
Center location
Radius of the polygon
Inscribed in a circle or Circumscribed about a circle
R
R
Sides = 6
Sides = 6
Inscribed
Circumscribed
Tangents
Drawing a Circle Tangent to a
Line
R
Center of Circle
Tangent Point
Offset
Given Line
Drawing a Tangent to Two Circles
Tangent Points
C1
C2
T
Tangent Points
T
C1
C2
T
T
Tangent to Two Arcs or Circles
Only One Tangent Point
C1
C2
Drawing a Tangent Arc in a
Right Angle
Required information prior to the
construction of an Arc Tangent to a line:
1.
Radius of the desired Arc = R
Offset
R
R
R
Offset
Given Right Angle
Drawing Tangent Arcs:
Acute & Obtuse Angles
Required information prior to
the construction of an Arc
Tangent to a line:
Offset
T
R
Offset
R
R
Acute Angle
Acute Angle Example
Radius of the desired Arc = R
Offset
T
Offset
R
T
Obtuse Angle
T
Obtuse Angle Example
Arc Tangent to:
an Arc and a Straight Line
Offset
RG+RD
Required information prior to the
construction of an Arc Tangent to
a line & Arc:
Given Arc
RG
Radius of the desired Arc = RD
T
Offset
RD
RD
T
Given Line
Arc Tangent to:
an Arc and a Straight Line
Required information prior to
the construction of an Arc
Tangent to a line & Arc:
Given Arc
Radius of the desired Arc = RD
RG
Offset
RG-RD
T
Offset
RD
RD
T
Given Line
Arc Tangent to two Arcs
Required information prior to
the construction of an Arc
Tangent to a line & Arc:
Offset
RG+RD
Offset
RG’+RD Radius of the desired Arc = RD
T
RG
RG’
T
RD
Given Arcs
Arc Tangent to two Arcs
cont.
Offset
Required information prior to
the construction of an Arc
Tangent to Two Arcs:
RG+RD
Radius of the desired Arc = RD
RG
Offset
RG’-RD
T
Given Arcs
RD
T
RG’
Arc Tangent to Two Arcs
cont. Enclosing Both
RD
T
RG’
RG
T
RD-RG’
RD-RG
Given Arcs
Required
information prior
to the construction
of an Arc Tangent
to Two Arcs:
Radius of the
desired Arc = RD
Arc Tangent to Two Arcs &
Enclosing One
T
Given Arcs
RD
RG
T
Offset
RD+RG
RG’
RD-RG’
Required information
prior to the
construction of an
Arc Tangent to Two
Arcs:
Radius of the
desired Arc = RD
That’s All Folks!
Tangent Arcs – Obtuse Angles
Example
Tangent Arcs – Acute Angles
Example
Circles and Arcs
Polygons
Quadrilaterals
Triangles
Angles
Points and Lines